Test4 | Giới thiệu về xác suất
Một thử nghiệm có ba bước với ba kết quả có thể xảy ra cho bước đầu tiên, hai kết quả có thể xảy ra ở bước thứ hai và bốn kết quả có thể xảy ra ở bước thứ ba. Bao nhiêu kết quả thí nghiệm tồn tại cho toàn bộ thí nghiệm?
$3.2.4 = 24$
Có bao nhiêu cách chọn ba vật phẩm từ một nhóm sáu vật phẩm?
$C^6_3=20$
Có bao nhiêu cách chọn ba vật phẩm từ một nhóm sáu vật phẩm?
$P^6_3=120$
Xét phép thử tung một đồng xu ba lần.
A. Xây dựng sơ đồ cây cho thí nghiệm.
B. Liệt kê các kết quả thí nghiệm.
C. Xác suất của mỗi kết quả thí nghiệm là bao nhiêu?
A,B.
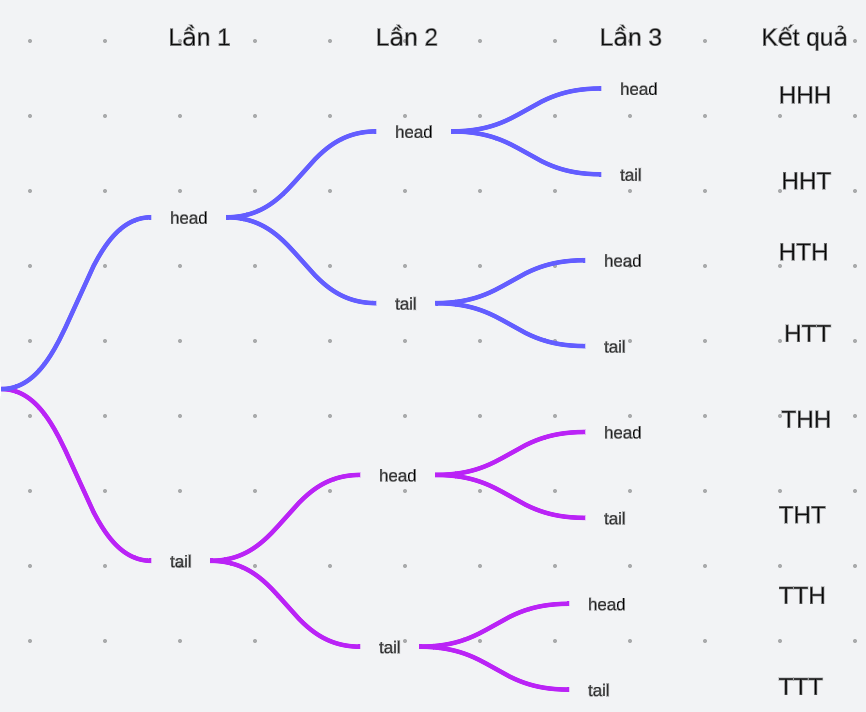
C. Xác suất của mỗi kết quả thí nghiệm là $\frac{1}{8}$
Một thí nghiệm có ba kết quả được lặp lại 50 lần và người ta biết rằng E1 xảy ra 20 lần, E2 xảy ra 13 lần và E3 xảy ra 17 lần. Gán xác suất cho các kết quả. Bạn đã sử dụng phương pháp nào?
$E1 xảy ra 20 lần, E2 xảy ra 13 lần và E3 xảy ra 17
$P(E1)=20/50,P(E2)=13/50,P(E3)=17/50$.
Dùng phương pháp tần số tương đối.
Xét phép thử chọn 1 quân bài từ bộ bài 52 lá.
A. Liệt kê sự kiện: lá Át (ace) được chọn.
B. Liệt kê sự kiện: lá Chuồn (club) được chọn.
C. Liệt kê sự kiện: lá face (jack, king, queen) được chọn.
D. Tìm xác suất của từng sự kiện ở các câu A,B,C.
S: spade (bích)
C: club (chuồn)
D: diamond (rô)
H: heart (cơ)
J: jack (bồi)
K: king (già)
Q: queen (đầm)
A. Liệt kê sự kiện: lá Át (ace) được chọn.
A={AS, AC, AH, AD}
B. Liệt kê sự kiện: lá Chuồn (club) được chọn.
B={AC, 2C, 3C, …, 10C, JC, KC, QC}
C. Liệt kê sự kiện: lá face (jack, king, queen) được chọn.
C={$JS, JC, JD, JH, KS, KC, KD, KH, QS, QC, QD, QH$}
D. Tìm xác suất của từng sự kiện ở các câu A,B,C.
P(A) = 4/52
P(B)= 13/52
P(C) = 12/52
Xét thí nghiệm tung một cặp xúc xắc. Giả sử chúng ta quan tâm đến tổng giá trị mặt xuất hiện trên xúc xắc.
A. Có tất cả bao nhiêu kết quả thí nghiệm? Liệt kê chúng.
B. Tính xác suất để đạt giá trị là 7.
C. Giá trị chẵn có xuất hiện thường xuyên hơn giá trị lẻ không?
A. Có tất cả bao nhiêu kết quả thí nghiệm? Liệt kê chúng.
$\Omega =$ {11, 12, …, 16, 21,… …, 66}. Có 6.6 = 36 kết quả.
B. Tính xác suất để đạt giá trị là 7.
7 = 1+6 = 6+1 = 2+5 = 5+2 = 3+4= 4+3.
Xác suất để đạt giá trị 7 là: $\frac{6}{36}$.
C. Giá trị chẵn có xuất hiện thường xuyên hơn giá trị lẻ không?
Các giá trị chẵn:
2 = 1+1
4 = 1+3 = 3+1 = 2+2
6 = 1+5 = 5+1 = 2+4 = 4+2 = 3+3
8 = 2+6 = 6+2 = 3+5 = 5+3 = 4+4
10 = 4+6 = 6+4 = 5+5
12 = 6+6
Số kết quả đạt giá trị chẵn là 18.
Xác suất để đạt giá trị chẵn là: $\frac{18}{36}$.
Các kết quả còn lại cho ra kết quả lẻ nên có số kết quả là: 36-18 = 18.
Xác suất để đạt giá trị lẻ là: $\frac{18}{36}$.
Vậy giá trị chẵn hay lẻ đều xuất hiện thường xuyên như nhau.
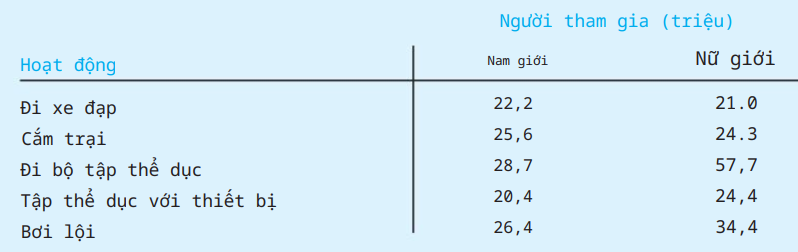
A. Đối với một phụ nữ được chọn ngẫu nhiên, hãy ước tính xác suất tham gia vào mỗi hoạt động thể thao.
B. Đối với một nam giới được chọn ngẫu nhiên, hãy ước tính xác suất tham gia vào mỗi hoạt động thể thao.
C. Đối với một người được chọn ngẫu nhiên, xác suất người đó tham gia đi bộ tập thể dục là bao nhiêu?
D. Giả sử bạn tình cờ nhìn thấy một người đi tập thể dục đi ngang qua. Xác suất là gì nếu người đi bộ là phụ nữ? Xác suất người đi bộ là đàn ông là bao nhiêu?
Nam: 120,9 triệu người.
Nữ: 127,6 triệu người.
Tổng: 248.5 triệu người.
A,B,C
| người tham gia | xác suất | |||||
| hoạt động | nam | nữ | hoạt động | nam | nữ | hoạt động |
| đi xe đạp | 22.2 | 21 | 43.2 | 0.089336 | 0.084507 | 0.173843 |
| cắm trại | 25.6 | 24.3 | 49.9 | 0.103018 | 0.097787 | 0.200805 |
| đi bộ tập thể dục | 28.7 | 57.7 | 86.4 | 0.115493 | 0.232193 | 0.347686 |
| tập thể dục với thiết bị | 20.4 | 24.4 | 44.8 | 0.082093 | 0.098189 | 0.180282 |
| bơi lội | 26.4 | 34.4 | 60.8 | 0.106237 | 0.138431 | 0.244668 |
D.
| người tham gia | xác suất | ||||
| hoạt động | nam | nữ | hoạt động | nam | nữ |
| đi bộ tập thể dục | 28.7 | 57.7 | 86.4 | 0.332176 | 0.667824 |
Một cuộc khảo sát yêu cầu các cựu sinh viên trả lời cho biết liệu trải nghiệm tổng thể của họ có thấp hơn mong đợi, đáp ứng mong đợi hay vượt qua mong đợi hay không. Kết quả cho thấy 4% số người được hỏi không đưa ra phản hồi, 26% cho biết trải nghiệm của họ không như mong đợi và 65% số người được hỏi cho biết trải nghiệm của họ đáp ứng mong đợi.
A. Nếu chúng ta chọn ngẫu nhiên một cựu sinh viên, xác suất để cựu sinh viên đó nói rằng trải nghiệm của họ vượt qua sự mong đợi là bao nhiêu?
B. Nếu chúng ta chọn ngẫu nhiên một cựu sinh viên thì xác suất mà cựu sinh viên đó sẽ nói trải nghiệm của họ đáp ứng hoặc vượt qua sự mong đợi là bao nhiêu?
A. Nếu chúng ta chọn ngẫu nhiên một cựu sinh viên, xác suất để cựu sinh viên đó nói rằng trải nghiệm của họ vượt qua sự mong đợi là: 100% – 4% – 26% – 65% = 4%.
B. Nếu chúng ta chọn ngẫu nhiên một cựu sinh viên thì xác suất mà cựu sinh viên đó sẽ nói trải nghiệm của họ đáp ứng hoặc vượt qua sự mong đợi là: 5% + 65% = 70%.
Thông tin về quỹ tương hỗ do Morningstar Investment Research cung cấp bao gồm loại quỹ tương hỗ (Vốn chủ sở hữu trong nước, Vốn chủ sở hữu quốc tế hoặc Thu nhập cố định) và xếp hạng Morningstar cho quỹ. Xếp hạng được thể hiện từ 1 sao (xếp hạng thấp nhất) đến 5 sao (xếp hạng cao nhất). Mẫu gồm 25 quỹ tương hỗ được chọn từ Morningstar Funds500 (2008).
Số liệu sau đây đã thu được:
- 16 quỹ tương hỗ là quỹ Vốn cổ phần trong nước.
- 13 quỹ tương hỗ được xếp hạng 3 sao trở xuống.
- 7 quỹ đầu tư trong nước được xếp hạng 4 sao.
- 2 quỹ đầu tư trong nước được xếp hạng 5 sao.
Giả sử rằng một trong 25 quỹ tương hỗ này sẽ được chọn ngẫu nhiên để tìm hiểu thêm về quỹ tương hỗ và chiến lược đầu tư của quỹ đó.
A. Xác suất lựa chọn quỹ đầu tư trong nước là bao nhiêu?
B. Xác suất chọn một quỹ có xếp hạng 4 sao hoặc 5 sao là bao nhiêu?
C. Xác suất để chọn được một quỹ vừa là quỹ Vốn cổ phần trong nước vừa là quỹ được xếp hạng 4 sao hoặc 5 sao là bao nhiêu?
D. Xác suất để lựa chọn quỹ là quỹ Vốn cổ phần trong nước hoặc quỹ với xếp hạng 4 sao hay 5 sao là bao nhiêu?
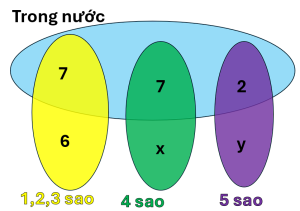
x+y = 3.
A. Xác suất lựa chọn quỹ đầu tư trong nước là: 16/25.
B. Xác suất chọn một quỹ có xếp hạng 4 sao hoặc 5 sao là:12/25.
C. Xác suất để chọn được một quỹ vừa là quỹ Vốn cổ phần trong nước vừa là quỹ được xếp hạng 4 sao hoặc 5 sao là: 10/25.
D. Xác suất để lựa chọn quỹ là quỹ Vốn cổ phần trong nước hoặc quỹ với xếp hạng 4 sao hay 5 sao là: 19/25.
Khảo sát người đăng ký tạp chí cho thấy 45,8% thuê xe trong 12 tháng qua vì lý do kinh doanh, 54% thuê xe trong 12 tháng qua vì lý do cá nhân và 30% thuê xe trong 12 tháng qua cho cả doanh nghiệp và lý do cá nhân.
A. Xác suất để một người đăng ký thuê một chiếc ô tô trong 12 tháng qua lý do kinh doanh hay cá nhân là bao nhiêu?
B. Xác suất để một người đăng ký không thuê xe trong 12 tháng qua vì lý do kinh doanh hoặc cá nhân là bao nhiêu?
chiếc ô tô trong 12 tháng qua là bao nhiêu?
A. Xác suất để một người đăng ký thuê một chiếc ô tô trong 12 tháng qua lý do kinh doanh hay cá nhân là: 45,8% + 54% – 30% = 69,8%.
B. Xác suất để một người đăng ký không thuê xe trong 12 tháng qua vì lý do kinh doanh hoặc cá nhân là: 100% – 69,8% = 30,2%.
Xem xét tình huống của tình trạng thăng tiến của nam và nữ sĩ quan trong lực lượng cảnh sát đô thị lớn ở miền đông Hoa Kỳ. Lực lượng cảnh sát bao gồm 1200 sĩ quan, 960 nam và 240 nữ. Trong hai năm qua, 324 sĩ quan trong lực lượng cảnh sát đã được thăng chức. cụ thể Cơ cấu thăng tiến của sĩ quan nam và nữ được trình bày trong Bảng sau:
| nam | nữ | tổng | |
| được thăng chức | 288 | 36 | 324 |
| không được thăng chức | 672 | 204 | 876 |
| tổng | 960 | 240 | 1200 |
Sau khi xem xét hồ sơ thăng chức, một ủy ban nữ sĩ quan đã đưa ra vụ án phân biệt đối xử với lý do 288 sĩ quan nam được thăng chức nhưng chỉ có 36 nữ sĩ quan được thăng cấp. Cơ quan cảnh sát lập luận rằng mức tương đối thấp số lượng thăng chức cho các sĩ quan nữ không phải do sự phân biệt đối xử mà là do thực tế là tương đối ít phụ nữ là thành viên của lực lượng cảnh sát. Chúng ta hãy chỉ ra cách sử dụng xác suất có điều kiện để phân tích cáo buộc phân biệt đối xử.
M: sự kiện một sĩ quan là một người đàn ông.
W: sự kiện một sĩ quan là một người phụ nữ.
A: sự kiện một sĩ quan được thăng chức.
$A^C$: sự kiện một sĩ quan được thăng chức.
Bảng xác suất:
| nam | nữ | tổng | |
| được thăng chức | 0.24 | 0.03 | 0.27 |
| không được thăng chức | 0.56 | 0.17 | 0.73 |
| tổng | 0.8 | 0.2 | 1 |
$P(A|M)=\frac{P(AM)}{P(M)}=\frac{0,24}{0,8}=0,3$
$P(A|W)=\frac{P(AW)}{P(W)}=\frac{0,03}{0,2}=0,15$.
Mặc dù bản thân việc sử dụng xác suất có điều kiện không chứng minh được rằng có sự phân biệt đối xử trong trường hợp này, nhưng các giá trị xác suất có điều kiện ủng hộ lập luận của các nữ sĩ quan.
Xem xét một bộ phận phát hành báo nơi được biết rằng 84% hộ gia đình trong một khu phố cụ thể đăng ký ấn bản hàng ngày của tờ báo. Nếu chúng ta đặt D biểu thị sự kiện một hộ gia đình đăng ký ấn bản hàng ngày, P(D) = 0,84. Ngoài ra, người ta biết rằng xác suất một hộ gia đình đã có đăng ký hàng ngày cũng đăng ký phiên bản Chủ nhật (sự kiện S) là 0,75; tức là P(SD) = 0,75. Xác suất để một hộ gia đình đăng ký cả ấn bản Chủ nhật và hàng ngày của tờ báo này là bao nhiêu?
$P(SD)=P(S|D).P(D)=0,75.0,84 = 0,63$
Giả sử có $P(A)=0,5,P(B)=0,6,P(AB)=0,4$.
A. Tính $P(A|B)$
B. Tính $P(B|A)$
C. Hai sự kiện $A,B$ có độc lập nhau không?
Giả sử có $P(A)=0,5,P(B)=0,6,P(AB)=0,4$.
A. $P(A|B)=P(AB)/P(B)=0,4/0,6\approx 0,67$
B. $P(B|A)=P(AB)/P(A)=0,4/0,5=0,8$
C. Vì $P(B|A)\not= P(B)$ nên $A,B$ không độc lập nhau.
Giả sử rằng chúng ta có hai sự kiện A và B loại trừ lẫn nhau. Giả sử thêm rằng $P(A)=0,4,P(B)=0,4$.
A. $P(AB)=$?
B. $P(A|B)=$?
C. Một sinh viên ngành thống kê lập luận rằng khái niệm các sự kiện loại trừ lẫn nhau và các sự kiện độc lập thực sự giống nhau, và rằng nếu các sự kiện loại trừ lẫn nhau thì chúng phải được độc lập. Bạn có đồng ý với điều này không? Sử dụng thông tin xác suất trong bài này để biện minh cho câu trả lời của bạn.
A. $P(AB)=0$.
B. $P(A|B)=P(AB)/P(B)=0$.
C. $P(A|B)\not=P(A)$ nên $A,B$ không độc lập.
Ngành công nghiệp ô tô đã bán được 657.000 xe tại Hoa Kỳ trong tháng 1 năm 2009 (Tạp chí Phố Wall, ngày 4 tháng 2 năm 2009). Khối lượng này đã giảm 37% so với tháng 1 năm 2008 khi điều kiện kinh tế tiếp tục suy giảm. Ba nhà sản xuất ô tô lớn của Mỹ—General Motors, Ford và Chrysler—bán được 280.500 xe, giảm 48% so với tháng 1 năm 2008. Bản tóm tắt doanh số bán hàng của nhà sản xuất ô tô và loại xe được bán được trình bày trong bảng sau:
| xe ô tô | xe tải nhẹ | |
| ở Mỹ | 87.4 | 193.1 |
| ngoài Mỹ | 228.5 | 148 |
Dữ liệu có trong hàng nghìn phương tiện. Các nhà sản xuất không phải của Mỹ dẫn đầu là Toyota, Honda và Nissan. Danh mục Xe tải nhẹ bao gồm xe bán tải, xe tải nhỏ, SUV và crossover.
A. Xây dựng một bảng xác suất chung cho những dữ liệu này và sử dụng bảng để trả lời các câu hỏi còn lại.
B. Xác suất cận biên là gì? Chúng cho bạn biết điều gì về các khả năng liên quan đến nhà sản xuất và loại xe được bán?
C. Nếu một chiếc xe được sản xuất bởi một trong những nhà sản xuất ô tô của Mỹ, xác suất phương tiện đó là một chiếc ô tô? Xác suất đó là một chiếc xe tải nhẹ là bao nhiêu?
D. Nếu một chiếc xe không được sản xuất bởi một trong những nhà sản xuất ô tô của Mỹ thì xác suất chiếc xe đó là một chiếc ô tô là bao nhiêu? Xác suất đó là một chiếc xe tải nhẹ là bao nhiêu?
E. Nếu chiếc xe đó là một chiếc xe tải nhẹ thì xác suất nó được sản xuất bởi các nhà sản xuất ô tô Mỹ là bao nhiêu?
A.
| xác suất | |||
| xe ô tô | xe tải nhẹ | tổng | |
| ở Mỹ | 0.13 | 0.29 | 0.43 |
| ngoài Mỹ | 0.35 | 0.23 | 0.57 |
| tổng | 0.48 | 0.52 | 1.00 |
B. Xác suất cận biên: nằm ở cột cuối và dòng cuối.
C.
M: xe được sản xuất ở Mỹ.
F: xe được sản xuất ở ngoài nước Mỹ.
T: xe ô tô.
N: xe tải nhẹ.
$P(T|M)=\frac{P(TM)}{P(M)}=\frac{0,13}{0,43}\approx 0,31$.
$P(N|M)=\frac{P(NM)}{P(M)}=\frac{0,29}{0,43}\approx 0,69$.
D.
$P(T|F)=\frac{P(TF)}{P(F)}=\frac{0,35}{0,67}\approx 0,61$.
$P(N|F)=\frac{P(NF)}{P(F)}=\frac{0,23}{0,57}\approx 0,39$.
E.
$P(M|N)=\frac{P(NM)}{P(N)}=\frac{0,29}{0,52}\approx 0,57$.
Bộ Giao thông Vận tải Hoa Kỳ báo cáo rằng trong tháng 11, 83,4% Các chuyến bay của Southwest Airlines, 75,1% chuyến bay của US Airways và 70,1% chuyến bay của JetBlue đến đúng giờ (USA Today, 4/1/2007). Giả sử rằng việc thực hiện đúng thời gian này là áp dụng cho các chuyến bay đến phòng chờ A của Sân bay Quốc tế Rochester, và rằng 40% số khách đến phòng chờ A là các chuyến bay của Southwest Airlines, 35% là US Airways các chuyến bay và 25% là các chuyến bay JetBlue.
A. Xây dựng bảng xác suất chung gồm 3 hàng (hãng hàng không) và 2 cột (đúng giờ) so với đến muộn.
B. Một thông báo vừa được đưa ra rằng Chuyến bay 1424 sẽ đến cổng 20 ở phòng chờ A. Hãng hàng không có khả năng nhất cho chuyến đến này là gì?
C. Xác suất chuyến bay 1424 sẽ đến đúng giờ là bao nhiêu?
D. Giả sử có một thông báo nói rằng Chuyến bay 1424 sẽ đến muộn. Hãng hàng không có khả năng nhất cho chuyến đến này là gì? Hãng hàng không ít có khả năng nhất là gì?
A.
| đúng giờ | đến muộn | đến phòng chờ A | đến A đúng giờ | đến A muộn | |
| Southwest Airlines | 0.824 | 0.176 | 0.4 | 0.330 | 0.058 |
| US Airways | 0.751 | 0.249 | 0.35 | 0.263 | 0.065 |
| JetBlue | 0.701 | 0.299 | 0.25 | 0.175 | 0.052 |
B. Southwest Airlines
C. Xác suất chuyến bay 1424 sẽ đến đúng giờ là: 0,33+0,263+0,175 = 0,768.
D.
M: muộn
S:Southwest Airlines
U: US Airways
J: JetBlue
$P(M)=0,058+0,065+0,052=0,176$
$P(S|M)=P(SM)/P(M)=0,058/0,176\approx 0,33$
$P(U|M)=P(UM)/P(M)=0,065/0,176\approx 0,372$
$P(J|M)=P(JM)/P(M)=0,052/0,176\approx 0,298$
Theo nghiên cứu về Tiền tài chính xuyên thế hệ của Ameriprise, 9 trong số 10 bậc cha mẹ có con trưởng thành từ 20 đến 35 tuổi đã giúp đỡ con cái trưởng thành của họ một số vấn đề hỗ trợ tài chính từ trường đại học, xe hơi, tiền thuê nhà, tiện ích, nợ thẻ tín dụng và tiền đặt cọc mua nhà (Money, tháng 1 năm 2009). Bảng sau đây với dữ liệu mẫu nhất quán với nghiên cứu cho thấy số lần cha mẹ hỗ trợ tài chính cho con cái đã trưởng thành của họ để mua ô tô và trả tiền thuê nhà.
| Thuê nhà | |||
| yes | no | ||
| Mua xe | yes | 56 | 52 |
| no | 14 | 78 | |
A. Xây dựng bảng xác suất chung và sử dụng nó để trả lời các câu hỏi còn lại.
B. Sử dụng các xác suất cận biên để mua một chiếc ô tô và trả tiền thuê nhà, các bậc cha mẹ có nhiều khả năng hỗ trợ con cái đã trưởng thành của họ mua xe hoặc trả tiền thuê nhà? Bạn giải thích thế nào về xác
suất cận biên?
C. Nếu cha mẹ hỗ trợ tài chính để mua một chiếc ô tô, xác suất để người đó cha mẹ có hỗ trợ trả tiền thuê nhà là bao nhiêu?
D. Nếu cha mẹ không hỗ trợ tài chính để mua ô tô thì xác suất cha mẹ có hỗ trợ trả tiền thuê nhà là bao nhiêu?
E. Hỗ trợ tài chính để mua xe có độc lập với hỗ trợ tài chính để trả tiền thuê nhà không? Sử dụng xác suất để biện minh cho câu trả lời của bạn.
F. Xác suất để cha mẹ hỗ trợ tài chính cho con cái đã trưởng thành của họ là bao nhiêu? dren bằng cách giúp mua một chiếc ô tô hoặc trả tiền thuê nhà?
A, B
| Thuê nhà | ||||
| yes | no | |||
| Mua xe | yes | 0.28 | 0.26 | 0.54 |
| no | 0.07 | 0.39 | 0.46 | |
| 0.35 | 0.65 | |||
C.
X: mua xe
Y: không mua xe
A: thuê nhà
B: không thuê nhà
$P(A|X)=\frac{P(AX)}{P(X)}=\frac{0,28}{0,54}\approx 0,52$.
D.
$P(A|Y)=\frac{P(AY)}{P(Y)}=\frac{0,07}{0,46}\approx 0,15$.
E.
$P(A|X)\not=P(A)$.
Vậy, hỗ trợ tài chính để mua xe độc lập với hỗ trợ tài chính để trả tiền thuê nhà.
Cho $P(A_1)=0,4,P(A_2)=0,6,P(A_1A_2)=0,P(B|A_1)=0,2,P(B|A_2)=0,05$.
A. $A_1,A_2$ có loại trừ nhau không?
B. Tính $P(A_1B),P(A_2B)$.
C. Tính $P(B)$.
D. Tính $P(A_1|B),P(A_2|B)$.
Cho $P(A_1)=0,4,P(A_2)=0,6,P(A_1A_2)=0,P(B|A_1)=0,2,P(B|A_2)=0,05$.
A.
$P(A_1A_2)=0$ nên $A_1,A_2$ có loại trừ nhau.
B.
$P(A_1B)=P(B|A_1).P(A_1)=0,2.0,4=0,08$.
$P(A_2B)=P(B|A_2).P(A_2)=0,05.0,6=0,03$.
C.
Vì $A_1,A_2$ xung khắc và $P(A_1)+P(A_2)=1$ nên $A_1+A_2=\Omega$.
Do đó $P(B)=P(A_1B)+P(A_2B)=0,08+0,03=0,11$.
D.
$P(A_1|B)=\frac{P(A_1B)}{P(B)}=\frac{0,08}{0,11}\approx 0,72$.
$P(A_2|B)=\frac{P(A_2B)}{P(B)}=\frac{0,03}{0,11}\approx 0,27$.
Một công ty tư vấn đã nộp một hồ sơ dự thầu cho một dự án nghiên cứu lớn. Ban quản lý của công ty ban đầu cảm thấy họ có 50-50 cơ hội để nhận dự án. Tuy nhiên, cơ quan mà hồ sơ đã được nộp sau đó yêu cầu thông tin bổ sung về hồ sơ dự thầu. Kinh nghiệm trước đây cho thấy rằng cho 75% các dự thầu thành công và 40% các dự thầu không thành công, cơ quan yêu cầu thông tin bổ sung.
A. Xác suất trước của việc dự thầu thành công (tức là trước khi yêu cầu thông tin bổ sung)?
B. Xác suất có điều kiện của việc yêu cầu thông tin bổ sung nếu dự thầu cuối cùng sẽ thành công?
C. Tính xác suất hậu nghiệm rằng dự thầu sẽ thành công nếu có yêu cầu thông tin bổ sung.
Gọi:
S là sự kiện dự thầu thành công.
F là sự kiện yêu cầu thông tin bổ sung.
Xác suất trước của việc dự thầu thành công: P(S) = 0.5 (50–50 ).
Xác suất yêu cầu thông tin bổ sung nếu dự thầu cuối cùng sẽ thành công: $P(F|S) = 0,75$.
Xác suất yêu cầu thông tin bổ sung nếu dự thầu cuối cùng không thành công: $P(F|S^C) = 0,4$.
A. Xác suất trước của việc dự thầu thành công (tức là trước khi yêu cầu thông tin bổ sung): $P(S) = 0,5$.
B. Xác suất có điều kiện của việc yêu cầu thông tin bổ sung nếu dự thầu cuối cùng sẽ thành công: $P(F|S) = 0,75$.
C. Tính xác suất hậu nghiệm rằng dự thầu sẽ thành công nếu có yêu cầu thông tin bổ sung (sử dụng công thức Bayes): $P(S|F) = P(S) . P(F|S) / [P(S) . P(F|S) + P(S^C) . P(F|S^C)] = \frac{0,5 . 0,75}{0,5 . 0,75 + 0,5 . 0,4}\approx 0.652$.
Một ngân hàng địa phương đã xem xét lại chính sách thẻ tín dụng của mình với ý định thu hồi một số thẻ tín dụng. Trong quá khứ, khoảng 5% số chủ thẻ đã vỡ nợ, khiến ngân hàng không thể thu được số dư còn lại. Do đó, ban quản lý đã thiết lập một xác suất trước đó là 0.05 cho bất kỳ chủ thẻ cụ thể nào sẽ vỡ nợ. Ngân hàng cũng phát hiện rằng xác suất bỏ lỡ thanh toán hàng tháng là 0.20 đối với khách hàng không vỡ nợ. Tất nhiên, xác suất bỏ lỡ thanh toán hàng tháng đối với những người vỡ nợ là 1.
a. Cho biết một khách hàng đã bỏ lỡ một hoặc nhiều lần thanh toán hàng tháng, tính xác suất hậu nghiệm rằng khách hàng sẽ vỡ nợ.
b. Ngân hàng muốn thu hồi thẻ nếu xác suất một khách hàng sẽ vỡ nợ lớn hơn 0.20. Liệu ngân hàng có nên thu hồi thẻ nếu khách hàng bỏ lỡ thanh toán hàng tháng không? Tại sao hoặc tại sao không?
A: vỡ nợ
P(A)=0,05
B: bỏ lỡ thanh toán
P(B|A^C)=0,2
P(B|A)=1
a.
P(A|B)=P(AB)/P(B)=P(B|A).P(A) / P(B|A).P(A)+P(B|A^C).P(A^C)=1.0,05 / 1.0,05+0,2.0,95=0,208
b.
Nên thu hồi.
Xe nhỏ tiết kiệm nhiên liệu hơn, nhưng chúng không an toàn bằng các loại xe lớn hơn. Xe nhỏ chiếm 18% số xe trên đường, nhưng các vụ tai nạn liên quan đến xe nhỏ dẫn đến 11,898 ca tử vong trong một năm gần đây (Reader’s Digest, tháng 5 năm 2000). Giả sử xác suất một xe nhỏ bị liên quan đến một vụ tai nạn là 0.18. Xác suất một vụ tai nạn liên quan đến xe nhỏ dẫn đến tử vong là 0.128 và xác suất một vụ tai nạn không liên quan đến xe nhỏ dẫn đến tử vong là 0.05. Giả sử bạn biết về một vụ tai nạn dẫn đến tử vong. Xác suất một xe nhỏ bị liên quan là bao nhiêu? Giả sử khả năng gặp tai nạn là độc lập với kích thước của xe.
A: xe nhỏ tai nạn
P(A)=0.18
B: tử vong
$P(B|A)=0.128$
$P(B|A^C)=0.05$
$P(A|B)=P(AB) / P(B) = P(B|A).P(A) / P(B|A).P(A)+P(B|A^C).P(A^C)= 0.128 * 0.18 / 0.128*0.18+0.05*0.82=0.36$
Hội đồng Giáo dục Mỹ báo cáo rằng 47% sinh viên năm nhất đại học nhận bằng và tốt nghiệp trong vòng năm năm (Associated Press, ngày 6 tháng 5 năm 2002). Giả sử hồ sơ tốt nghiệp cho thấy phụ nữ chiếm 50% số sinh viên tốt nghiệp trong vòng năm năm, nhưng chỉ chiếm 45% số sinh viên không tốt nghiệp trong vòng năm năm. Các sinh viên chưa tốt nghiệp trong vòng năm năm hoặc bỏ học hoặc vẫn đang làm việc để hoàn thành bằng cấp của họ.
a. Đặt A1 – sinh viên tốt nghiệp trong vòng năm năm A2 – sinh viên không tốt nghiệp trong vòng năm năm W – sinh viên là nữ Sử dụng thông tin đã cho, giá trị của P(A1), P(A2), P(W|A1), và P(W|A2) là gì?
b. Xác suất một sinh viên nữ sẽ tốt nghiệp trong vòng năm năm là bao nhiêu?
c. Xác suất một sinh viên nam sẽ tốt nghiệp trong vòng năm năm là bao nhiêu? d. Với kết quả trước đó, phần trăm phụ nữ và phần trăm nam trong lớp sinh viên năm nhất là bao nhiêu?
a.
| A1 | 47% |
| A2 | 53% |
| W|A1 | 50% |
| W|A2 | 45% |
b.
P(WA1)=P(W|A1).P(A1)=50%.47%=23.5%
c.
M: sinh viên nam
P(M|A1)=1-P(W|A1)=1-50%=50%
P(MA1)=P(M|A1).P(A1)=50%.47%=23.5%
d.
P(WA2)=P(W|A2).P(A2)=45%.53%=23.85%
P(W)=P(WA1)+P(WA2)=23.5%+23.85%=47.35%
P(M)=1-P(W)=1-47.35%=52.65%
Trong một bài báo về các lựa chọn đầu tư, tạp chí Money đưa tin rằng cổ phiếu dược phẩm cung cấp tiềm năng tăng trưởng dài hạn, với hơn 50% dân số trưởng thành tại Hoa Kỳ sử dụng thuốc theo đơn thường xuyên. Đối với người trưởng thành từ 65 tuổi trở lên, 82% sử dụng thuốc theo đơn thường xuyên. Đối với người trưởng thành từ 18 đến 64 tuổi, 49% sử dụng thuốc theo đơn thường xuyên. Nhóm tuổi từ 18 đến 64 tuổi chiếm 83.5% trong số dân số trưởng thành (Tổng quan thống kê của Hoa Kỳ, 2008).
a. Xác suất một người trưởng thành được chọn ngẫu nhiên là 65 tuổi trở lên là bao nhiêu?
b. Cho biết một người trưởng thành sử dụng thuốc theo đơn thường xuyên, xác suất một người đó là 65 tuổi trở lên là bao nhiêu?
a.
| 18 đến 64 | N | 83.50% |
| trên 65 | L | 16.50% |
| dùng thuốc theo đơn | T |
b.
P(TN)=P(T|N).P(N)=49% . 83.5% =40.915%
P(TL)=P(T|L).P(L)=82% . 16.5% =13.53%
P(T)=P(TL)+P(TN)=13.53% + 40.915% =54.445%
P(L|T)=P(TL)/P(T)=13.53% / 54.445%=24.85%
Bảng khảo sát của The Wall Street Journal/Harris Personal Finance hỏi 2082 người trưởng thành xem họ có sở hữu một căn nhà không (trang web All Business, ngày 23 tháng 1 năm 2008). Tổng cộng 1249 người tham gia khảo sát đã trả lời “Có”. Trong số 450 người tham gia khảo sát thuộc nhóm tuổi 18-34, có 117 người trả lời “Có”.
a. Xác suất một người tham gia khảo sát sở hữu một căn nhà là bao nhiêu?
b. Xác suất một người tham gia khảo sát trong nhóm tuổi 18-34 sở hữu một căn nhà là bao nhiêu?
c. Xác suất một người tham gia khảo sát không sở hữu một căn nhà là bao nhiêu?
d. Xác suất một người tham gia khảo sát trong nhóm tuổi 18-34 không sở hữu một căn nhà là bao nhiêu?
| xác suất | |||
| người được hỏi | 2082 | ||
| có nhà | Y | 1249 | 59.99% |
| ko nhà | N | 833 | 40.01% |
| 18-34 tuổi | T | 450 | |
| Y|T | 117 | 26.00% | |
| N|T | 333 | 74.00% |
Vào đầu năm 2003, Tổng thống Bush đề xuất loại bỏ việc đánh thuế đối với cổ tức cho cổ đông với lý do đó là sự đánh thuế kép. Các công ty phải trả thuế trên lợi nhuận sau đó được trả dưới dạng cổ tức. Trong một cuộc khảo sát với 671 người Mỹ, TechnoMetrica Market Intelligence phát hiện rằng 47% ủng hộ đề xuất này, 44% phản đối, và 9% không chắc chắn (Investor’s Business Daily, ngày 13 tháng 1 năm 2003). Trong việc xem xét các phản ứng theo các đảng, cuộc khảo sát cho thấy 29% người Dân chủ ủng hộ, 64% người Cộng hòa ủng hộ, và 48% người Độc lập ủng hộ.
a. Có bao nhiêu người tham gia khảo sát ủng hộ việc loại bỏ thuế đối với cổ tức?
b. Xác suất có điều kiện ủng hộ đề xuất khi người tham gia khảo sát là Dân chủ là bao nhiêu?
c. Liên hệ đảng phái có phải là độc lập với việc người tham gia khảo sát ủng hộ đề xuất không?
d. Nếu chúng ta giả định phản ứng của mọi người phản ánh lợi ích cá nhân của họ, nhóm nào bạn tin sẽ hưởng lợi nhiều nhất từ việc thông qua đề xuất?
a.
| số người | 671 | |
| ủng hộ | 315.37 | 47% |
315.37≈ 316 người
b.
| dân chủ | |
| ủng hộ | 29% |
c.
| dân chủ | D |
| cộng hòa | C |
| độc lập | L |
| ủng hộ | U |
P(U|D)=29%
P(U|C)=64%
P(U|L)=48%
Tất cả đều khác P(U)=47% nên liên hệ đảng phái không độc lập với việc người tham gia khảo sát ủng hộ đề xuất.
d.
Nhóm người Cộng hòa (64% ủng hộ) sẽ hưởng lợi nhiều nhất nếu đề xuất được thông qua, vì họ có tỷ lệ ủng hộ cao nhất so với các đảng khác.
Một nghiên cứu về 31.000 ca nhập viện tại tiểu bang New York phát hiện rằng 4% số ca nhập viện dẫn đến chấn thương do điều trị gây ra. Một phần bảy trong số những chấn thương do điều trị gây ra này dẫn đến tử vong, và một phần tư là do sơ suất. Đơn kiện về y khoa được nộp trong một trường hợp trên mỗi 7,5 trường hợp liên quan đến sơ suất, và thanh toán được thực hiện trong một trường hợp trên mỗi hai đơn kiện.
a. Xác suất một người nhập viện sẽ bị chấn thương do điều trị gây ra do sơ suất là bao nhiêu?
b. Xác suất một người nhập viện sẽ chết do chấn thương do điều trị gây ra là bao nhiêu?
c. Trong trường hợp chấn thương do điều trị gây ra do sơ suất, xác suất một đơn kiện y khoa sẽ được thanh toán là bao nhiêu?
a.
4% số ca nhập viện dẫn đến chấn thương do điều trị gây ra.
Trong số những chấn thương do điều trị:
- 1/4 do sơ suất
- 1/7 tử vong
Xác suất một người nhập viện sẽ bị chấn thương do điều trị gây ra do sơ suất là: 4% . 1/4 = 1%.
b.
Xác suất một người nhập viện sẽ chết do chấn thương do điều trị gây ra là: 4% . 1/7=0.57%
c.
| 7.5 sơ suất=1 bị kiện | |
| sơ suất | |
| bị kiện | 0.133333 |
| 1 thanh toán = 2 đơn kiện | |
| bị kiện | |
| thanh toán | 0.5 |
Trong trường hợp chấn thương do điều trị gây ra do sơ suất, xác suất một đơn kiện y khoa sẽ được thanh toán là: 1/7.5 . 1/2 = 6.67%.
