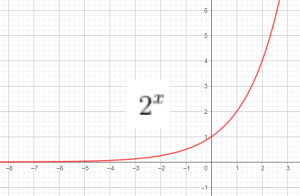
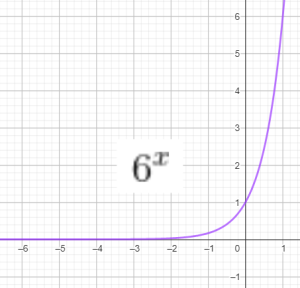
Toán 11 | Cơ bản
Chương 1.
1. Góc lượng giác
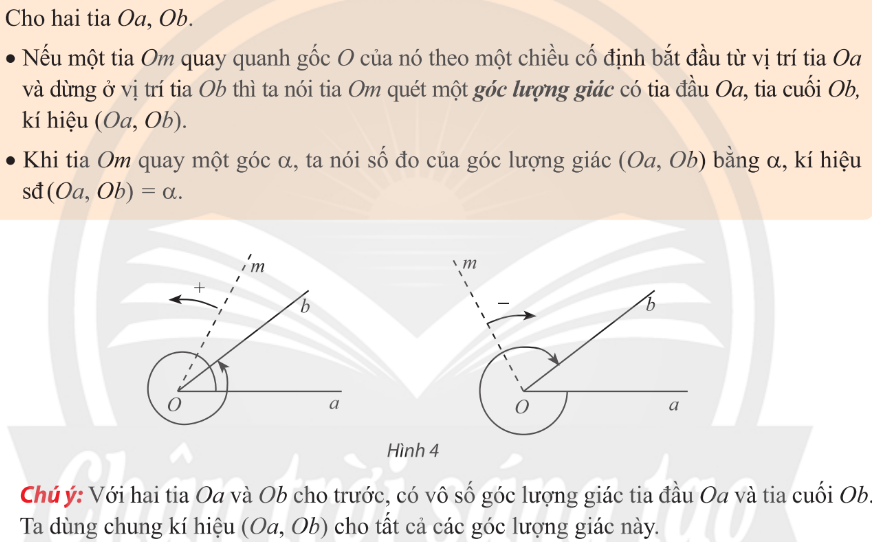
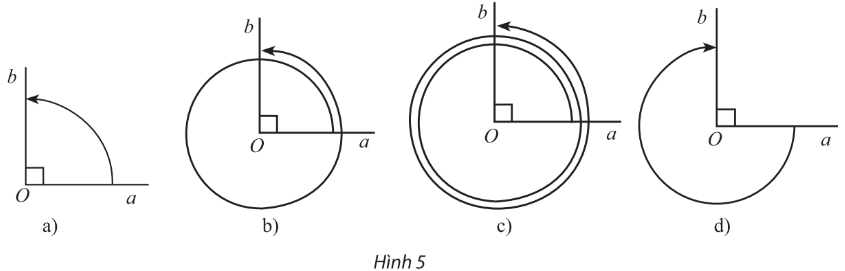

Hệ thức Chasles (đọc là Sa lơ):
$(Oa,Ob)+(Ob,Oc)=(Oa,Oc)+k360^o, (k\in \mathbb{Z})$
2. Đơn vị radian
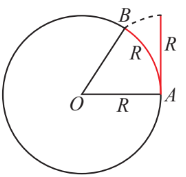 $\widehat{AOB}=1$ radian (viết tắt là rad)
$\widehat{AOB}=1$ radian (viết tắt là rad)
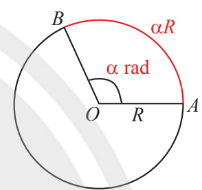 $180^o=\pi$ rad
$180^o=\pi$ rad

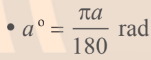

3. Đường tròn lượng giác
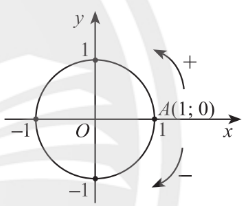


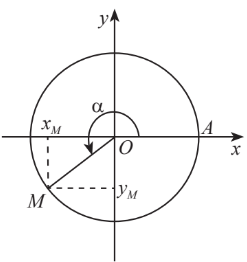
1. Giá trị lượng giác của góc

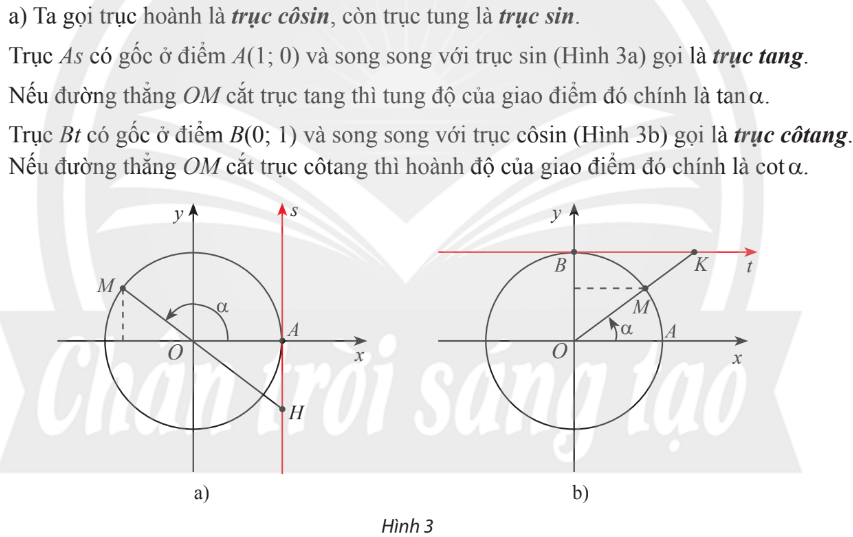

2. Tính giá trị lượng giác của 1 góc bằng máy tính
Lưu ý chọn đúng đơn vị trước khi tính.
3. Hệ thức cơ bản giữa các giá trị lượng giác
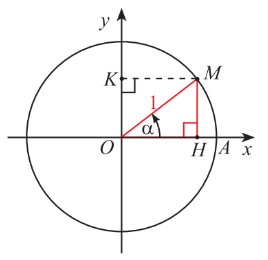
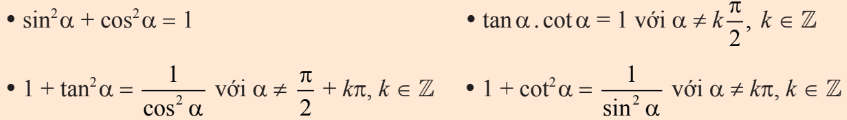
4. Giá trị lượng giác của góc có liên quan đặc biệt
Đối nhau:
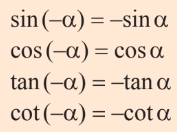
Hơn kém $\pi$:
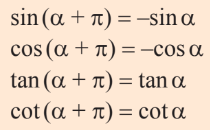
Bù nhau:
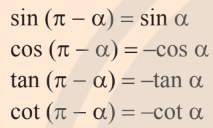
Phụ nhau:

1. Công thức cộng
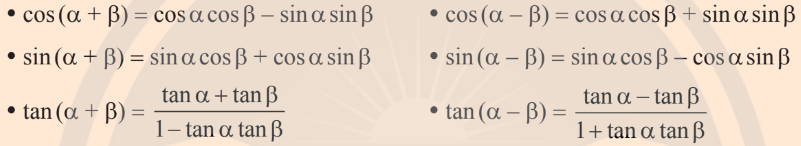
2. Công thức góc nhân đôi
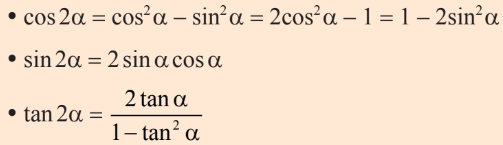
3. Công thức biến đổi tích thành tổng
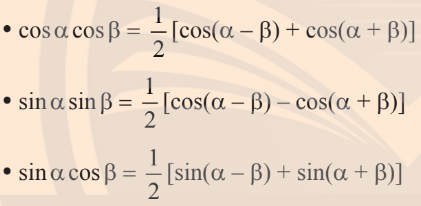
4. Công thức biến đổi tổng thành tích
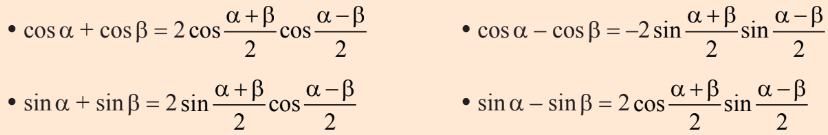
1. Hàm số lượng giác

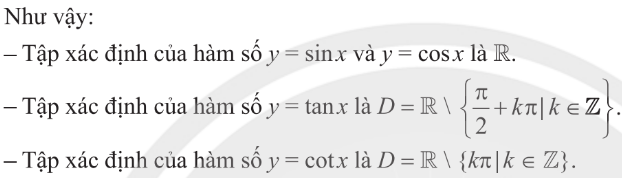
2. Hàm số chẵn, hàm số lẻ


3. Hàm số tuần hoàn


4. Đồ thị của hàm số lượng giác
Hàm $y=\sin x$
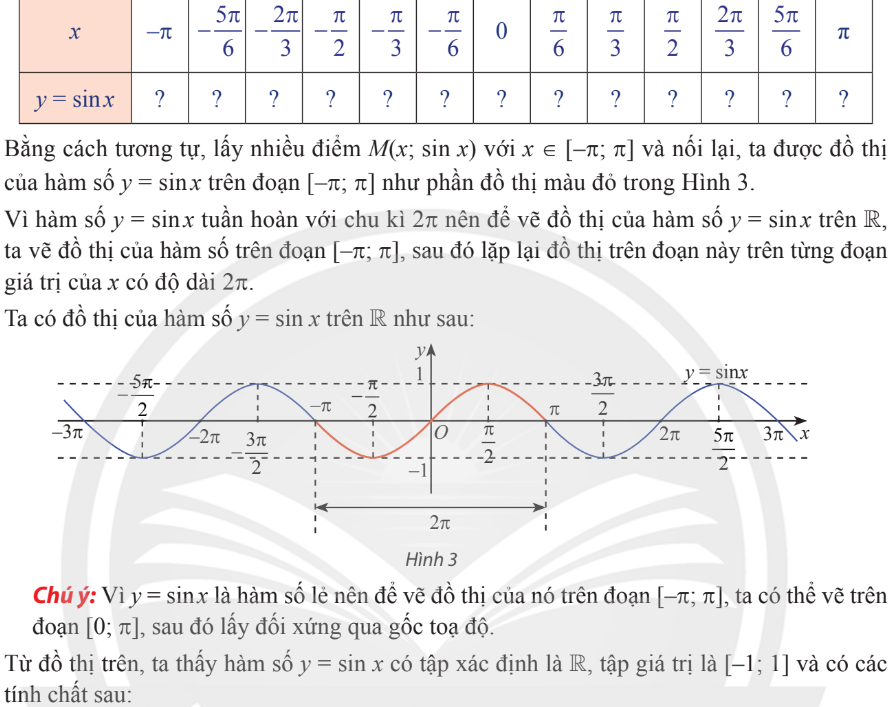
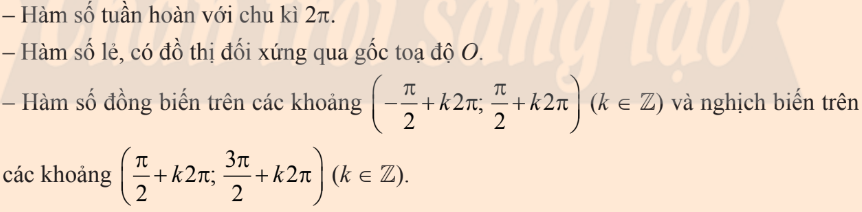
Hàm $y=\cos x$

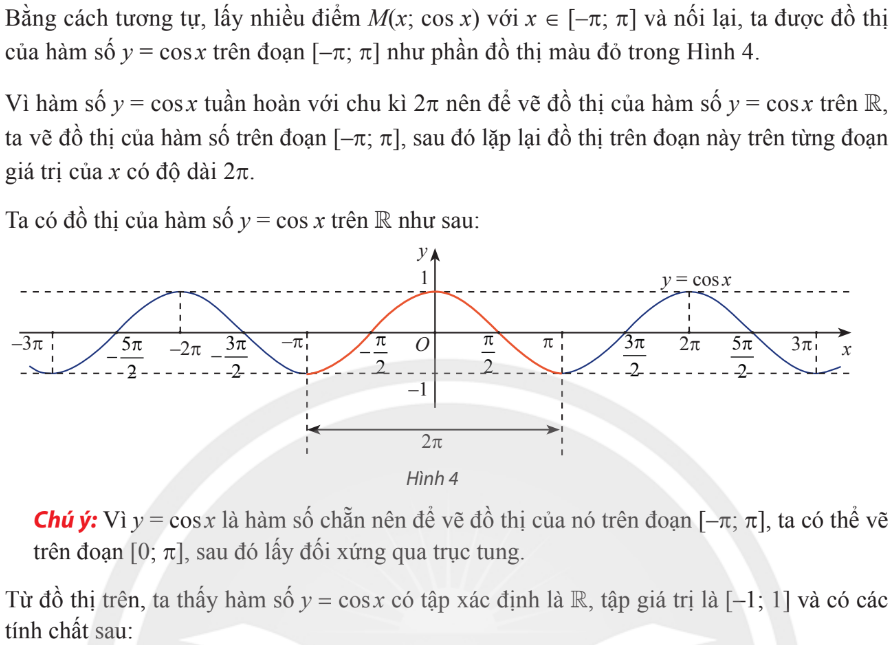

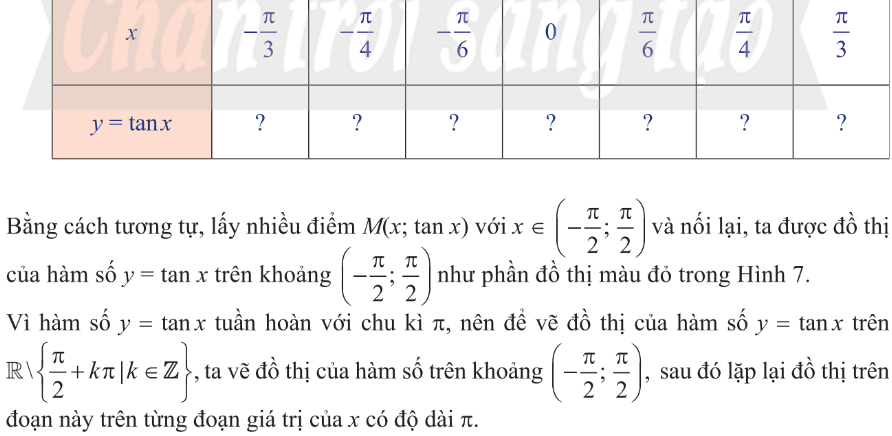
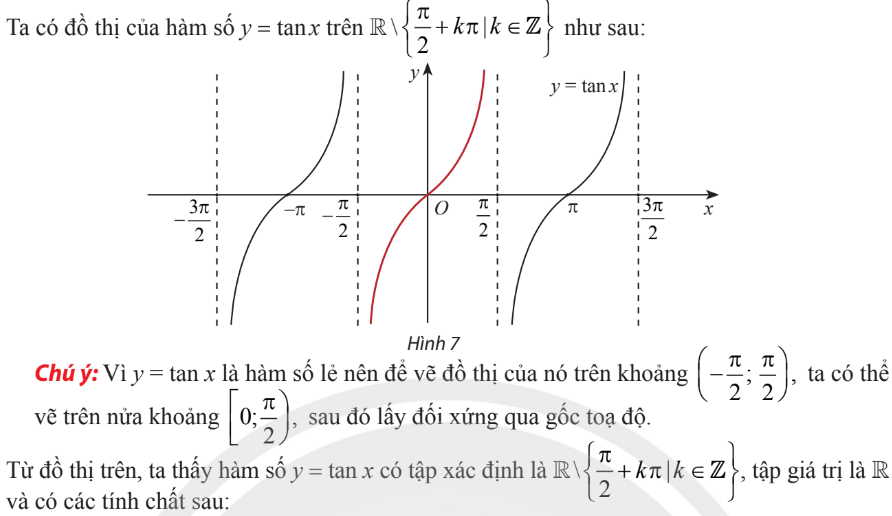
Hàm $y=\tan x$

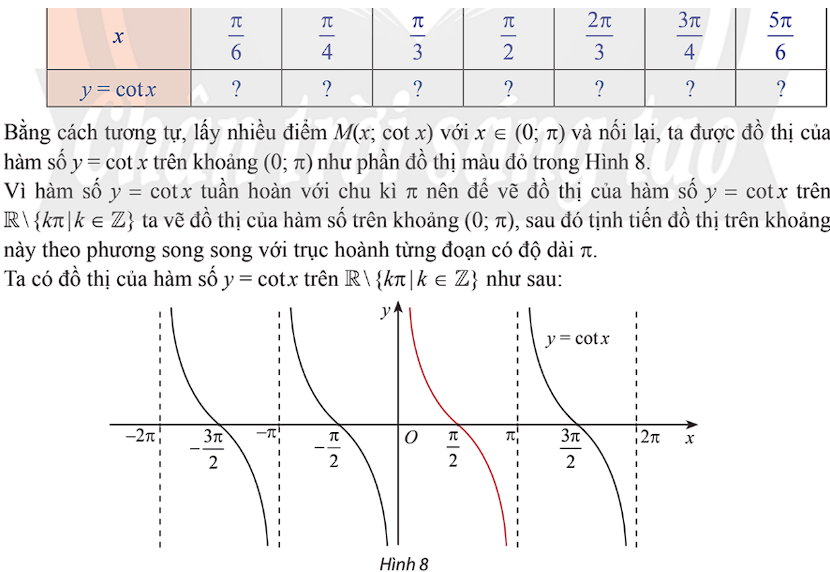
Hàm $y=\cot x$
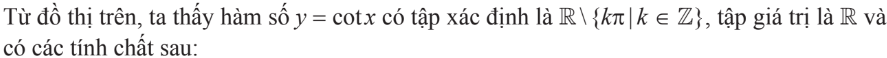

1. Phương trình tương đương
Hai phương trình tương đương nếu chúng có cùng tập nghiệm.

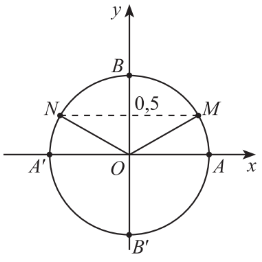
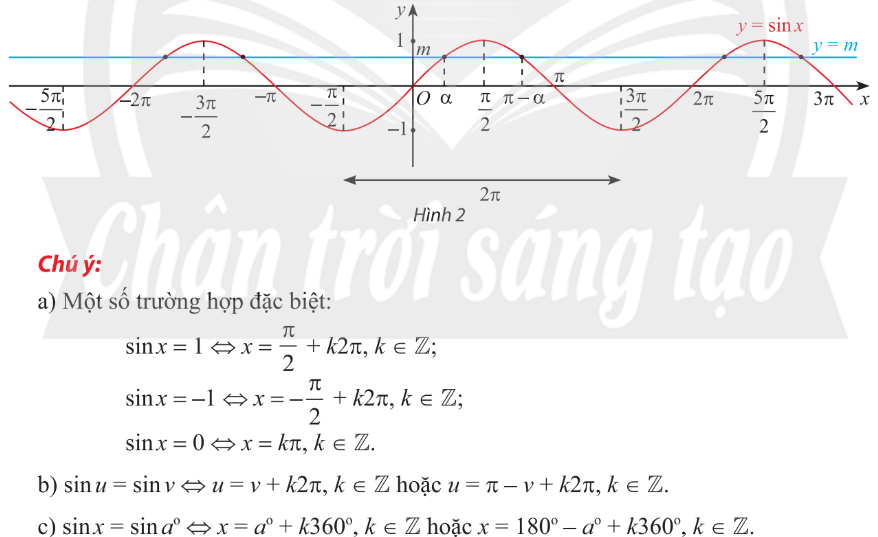
2. Phương trình $\sin x=m$

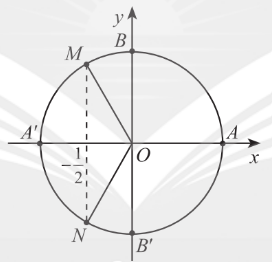
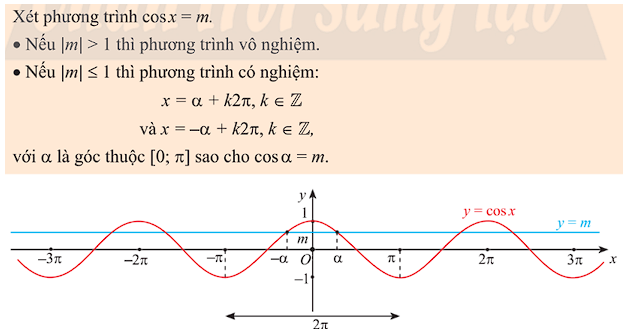
3. Phương trình $\cos x=m$
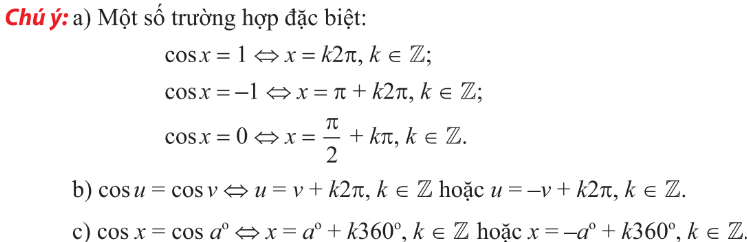
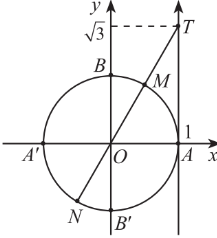
4. Phương trình $\tan x=m$
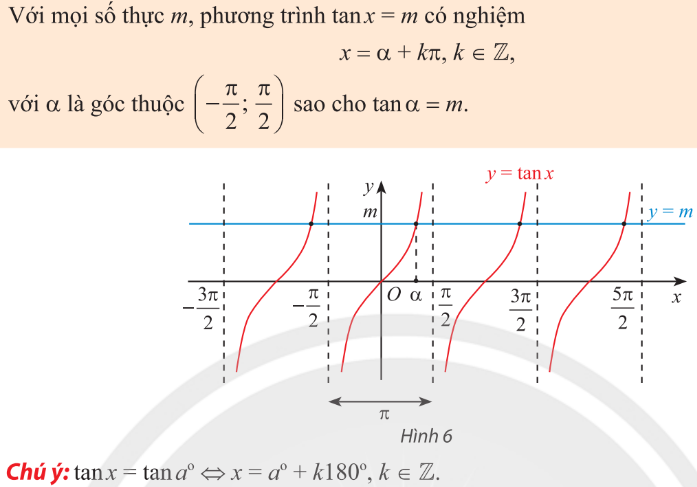
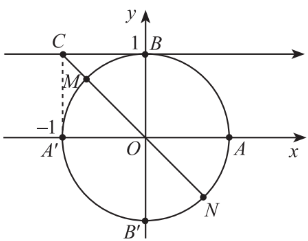
5. Phương trình $\cot x=m$
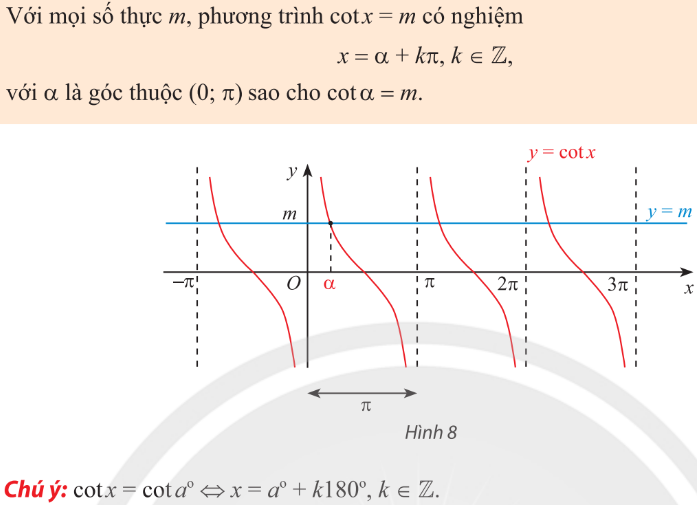
6. Giải phương trình lượng giác bằng máy tính
$\sin x=$-1/2
![]() .
.
Tương tự với $\cos, \tan, \cot$.
Chương 2.
1. Dãy số là gì


2. Cách xác định dãy số

3. Dãy số tăng, dãy số giảm

4. Dãy số bị chặn

5. Dãy số Fibonacci
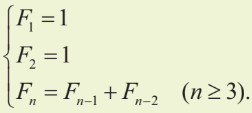
1. Cấp số cộng

2. Số hạng tổng quát của cấp số cộng
$u_n=u_1+(n-1)d, n\geq 2$.
3. Tổng của n số hạng đầu tiên của cấp số cộng


1. Cấp số nhân

2. Số hạng tổng quát của cấp số nhân
$u_n=u_1.q^{n-1}$.
3. Tổng của n số hạng đầu tiên của cấp số nhân
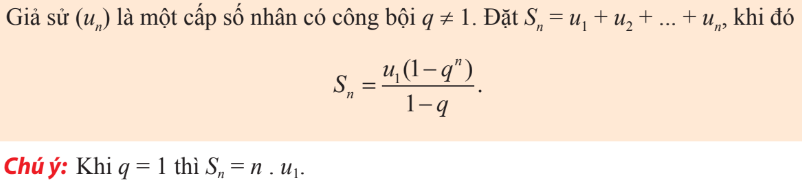
Chương 3.
1. Giới hạn hữu hạn của dãy số
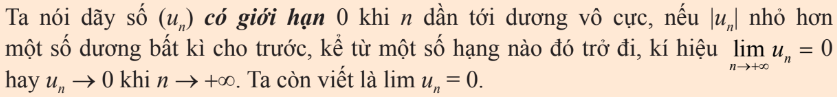


2. Các phép toán về giới hạn
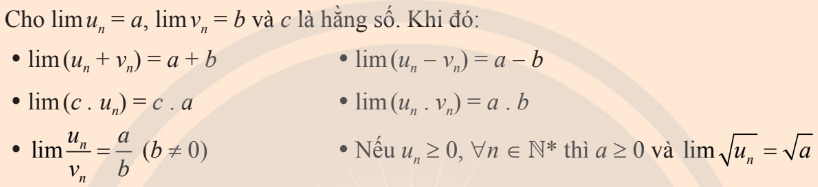
3. Tổng của cấp số nhân lùi vô hạn

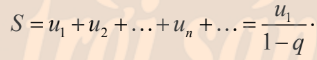
4. Giới hạn vô cực

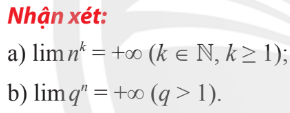
1. Giới hạn hữu hạn của hàm số tại 1 điểm
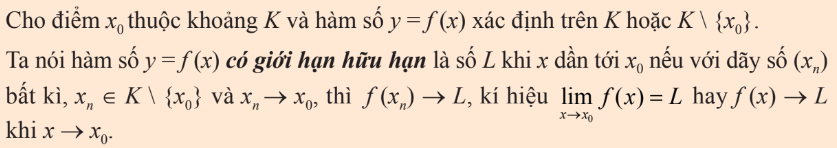
2. Các phép toán về giới hạn


3. Giới hạn 1 phía


4. Giới hạn hữu hạn của hàm số tại vô cực


5. Giới hạn vô cực của hàm số tại 1 điểm


1. Hàm số liên tục tại 1 điểm

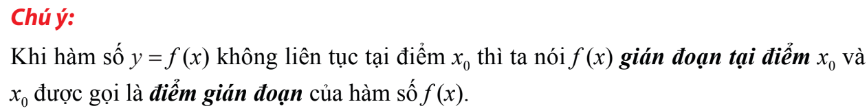
2. Hàm số liên tục trên 1 khoảng


3. Tính liên tục của hàm số sơ cấp


4. Tổng, hiệu, tích thương của hàm liên tục

Chương 4.
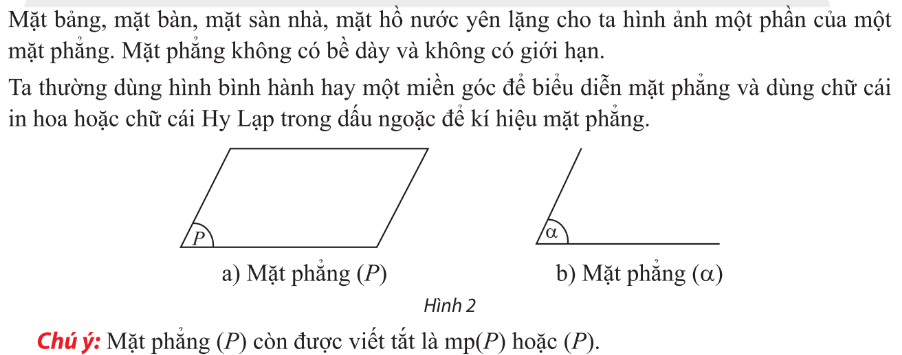
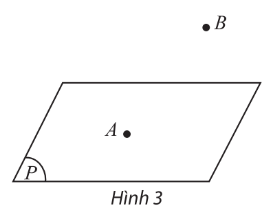
1. Mặt phẳng trong không gian



2. Các tính chất được thừa nhận
Tính chất 1:

Tính chất 2:

Tính chất 3:

Tính chất 4:

Tính chất 5:

Tính chất 6:
Trong mỗi mặt phẳng, các kết quả của hình học phẳng đều đúng.
3. Cách xác định mặt phẳng



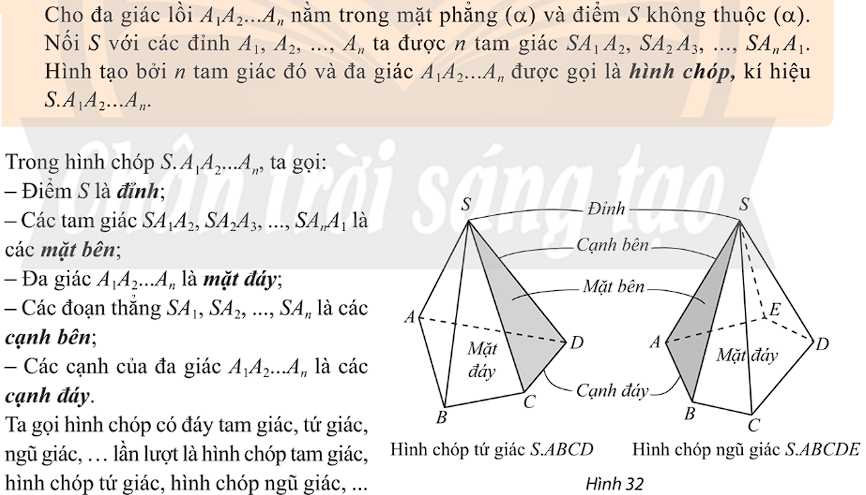
4. Hình chóp

1. Vị trí tương đối của 2 đường thẳng

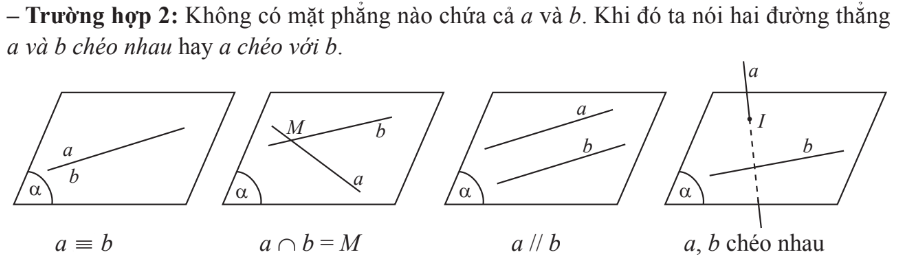

2. Tính chất cơ bản về 2 đường thẳng song song
Định lí 1:
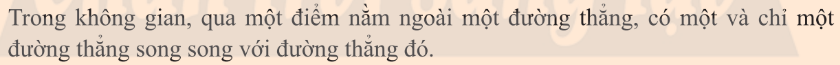
Định lí 2:
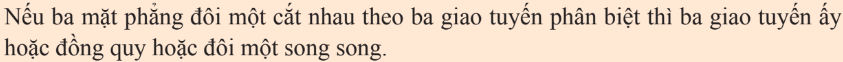
Hệ quả:
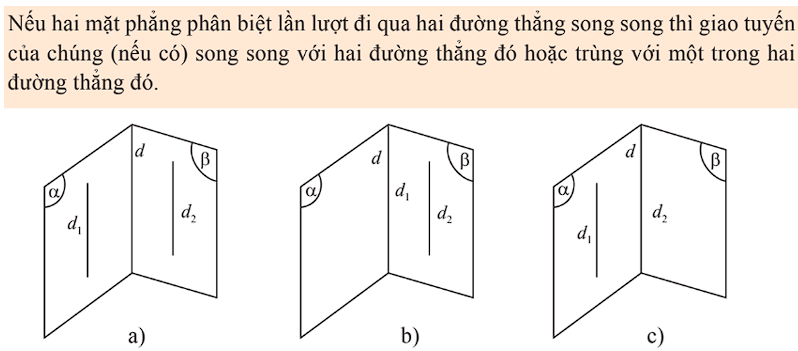
Định lí 3:

1. Đường thẳng song song với mặt phẳng

Đường thẳng $a$ song song với mặt phẳng $(P)$ nếu chúng không có điểm chung.
2. Điều kiện để 1 đường thẳng song song với 1 mặt phẳng

3. Tính chất cơ bản của đường thẳng và mặt phẳng song song



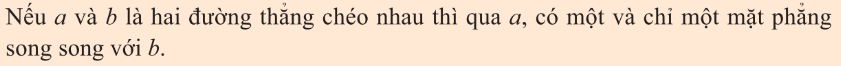
1. Hai mặt phẳng song song

2. Điều kiện để 2 mặt phẳng song song

3. Tính chất của 2 mặt phẳng song song

4. Định lí Thales trong không gian

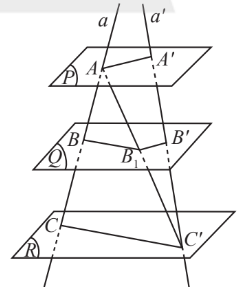
$ \frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{AC}{A’C’}$
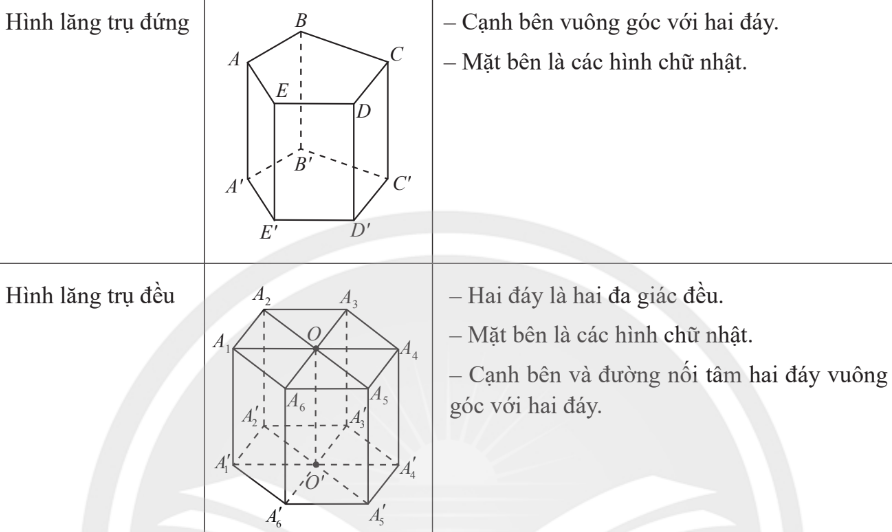
5. Hình lăng trụ và hình hộp
Hình lăng trụ


Hình hộp

1. Khái niệm phép chiếu song song

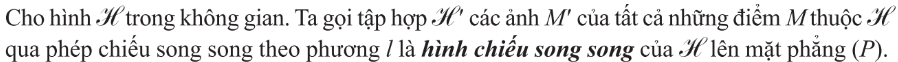
2. Các tính chất cơ bản của phép chiếu song song
Tính chất 1:

Tính chất 2:

Tính chất 3:

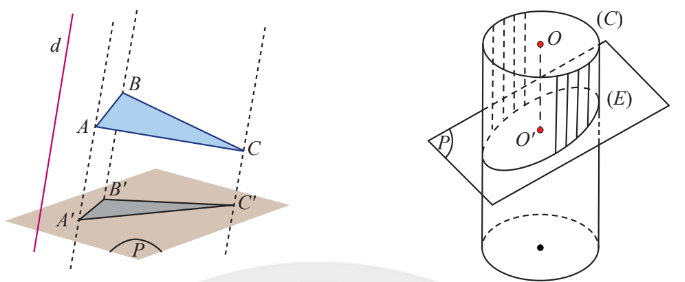
3. Hình biểu diễn của 1 hình không gian

Chương 5.
1. Số liệu ghép nhóm



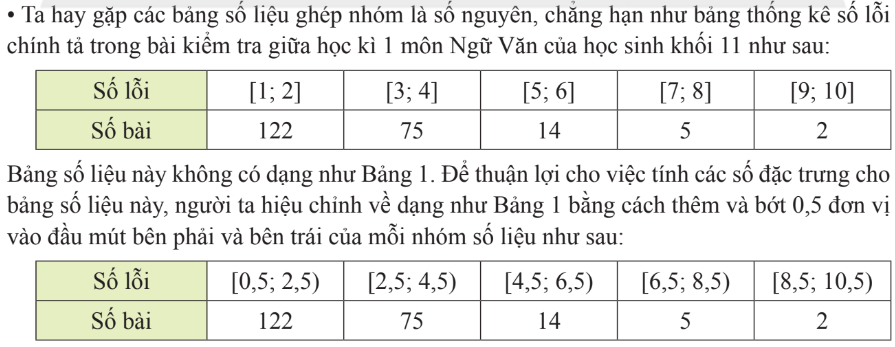
2. Số trung bình


3. Mốt (mode)


1. Trung vị


2. Tứ phân vị

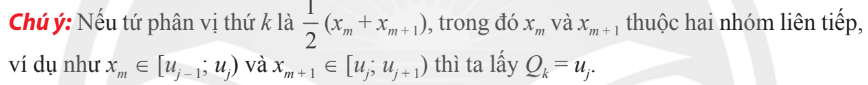

Chương 6.
1. Lũy thừa với số mũ nguyên
$a^n = \underset{n \text{ số }a}{\underbrace{a.a…a}}$
$a$ là cơ số, $n$ là số mũ.
$a^0=1$
$a^{-n}=\frac{1}{a^n}$
$0^0, 0^{-n}$ ko xác định.
Phương trình bậc lẻ (số mũ $n$ lẻ): $x^n=b$ có 1 nghiệm là $x=\sqrt[n]{b}$.
Phương trình bậc chẵn (số mũ $m$ chẵn): $x^m=d$
- nếu $d<0$ thì vô nghiệm
- nếu $d=0$ thì có 1 nghiệm $x=0$
- nếu $d>0$ thì có 2 nghiệm $x=\sqrt[m]{d}$ và $x=-\sqrt[m]{d}$
2. Căn bậc n
Cho $n$ là số nguyên dương.
Số $a$ là căn bậc $n$ của $b$ nếu $a^n=b$.

$\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$
$\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
$\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
$\sqrt[n]{a^n}=\begin{cases}
a& \text{nếu }n\text{ lẻ }\\
|a|& \text{nếu }n\text{ chẵn }
\end{cases}$
$\sqrt[n]{a^m}=(\sqrt[n]{a})^m$
3. Lũy thừa với số mũ hữu tỉ
$\displaystyle a^{\frac{m}{n}}=\sqrt[n]{a^m}$.
4. Lũy thừa với số mũ thực


5. Tính chất của phép tính lũy thừa
Cho $a,b$ dương. Ta có:
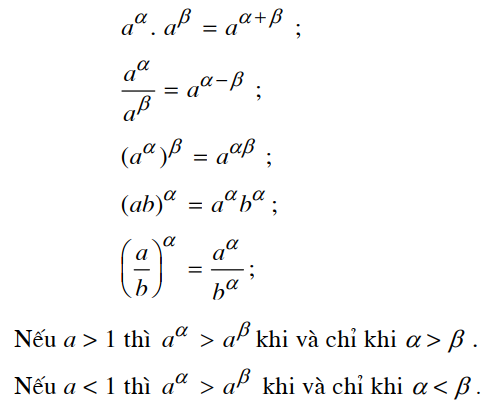
Bài tập:
Test10 | Lũy thừa
1. Khái niệm logarit
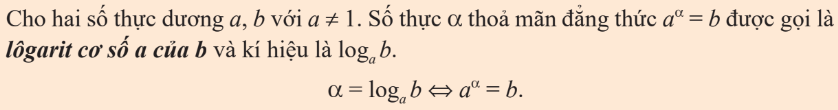
Nếu $a^x=b$ thì $x=\log_a b$.
Có thể nói hàm loagarit (log) là hàm để tìm số mũ.

$\log_a a^y=y$
Vì $a^0=1$ nên $\log_a 1=0$
Vì $a^1=a$ nên $\log_a a=1$
Nếu $\log_a b=x$ thì $a^x=b$. Suy ra $a^{\log_a b}=a^x=b$
2. Tính logarit bằng máy tính

với $e\approx 2,718$

3. Tính chất của phép tính logarit
$\log_a (b.c)=\log_a b + \log_a c$
$\log_a \frac{b}{c}=\log_a b – \log_a c$
$\log_a \frac{1}{x}=\log_a 1 – \log_a x = 0 – \log_a x = -\log_a x$
$\log_a b^x=x.\log_a b$ nếu $b>0$
$\log_a b^x=x.\log_a |b|$ nếu $b<0$
$\log_a \sqrt[n]{x}=\log_a \left ( x^{\frac{1}{n}} \right )=\frac{1}{n}.\log_a x$
4. Công thức đổi cơ số
$\log_a b = \frac{\log_c b}{\log_c a}$ với số $c$ dương và khác 1 tùy ý.
$\log_a b = \frac{\log_b b}{\log_b a}=\frac{1}{\log_b a}$
$\log_{(a^n)}x=\frac{1}{n}\log_a x$
Để ý:
- khi $a>1$:
- nếu $b>a$ thì $\log_a b=x>0$
- nếu $b<a$ thì $\log_a b=x<0$
- khi $1>a>0$:
- nếu $b>a$ thì $\log_a b=x<0$
- nếu $b<a$ thì $\log_a b=x>0$
Bài tập:
Test12 | Logarit
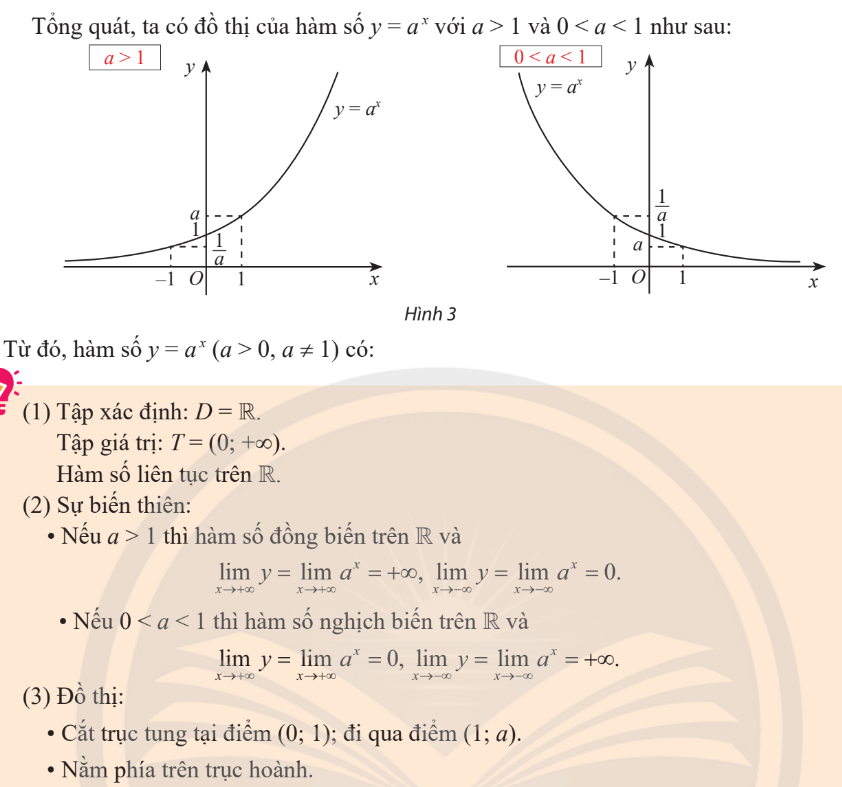
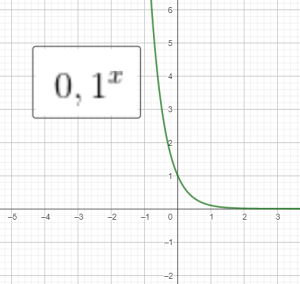
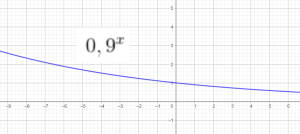
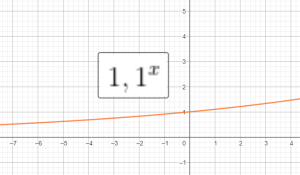
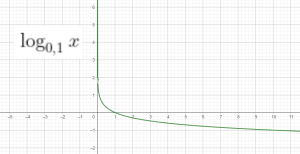
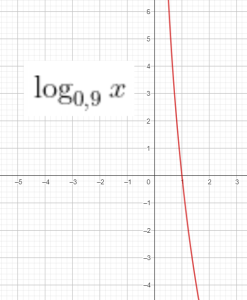
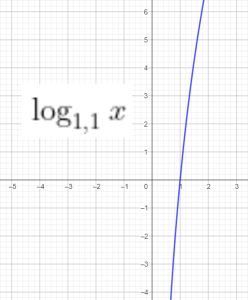
Hàm số logarit cơ số $a$:
$f(x)=\log_a x$ với $a$ dương, khác 1.

Đồ thị của 1 số hàm log:
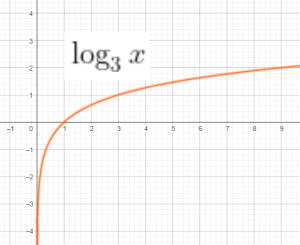
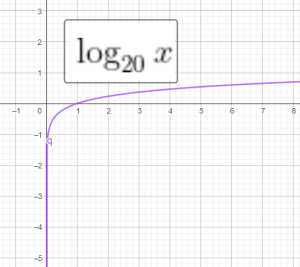
Bài tập:
Test14 | Hàm logarit
Phương trình $a^x=b$ với $a$ dương khác 1:
- nếu $b>0$ thì $x=\log_a b$
- nếu $b\leq 0$ thì vô nghiệm
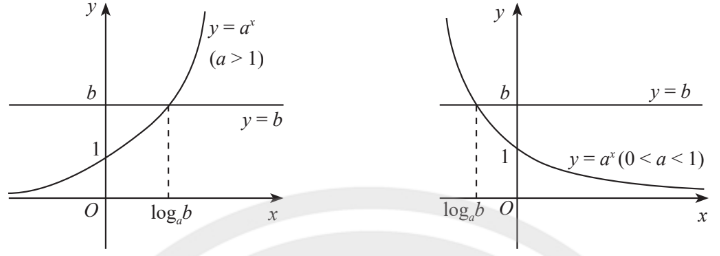
Bài tập:
Test15 | Phương trình mũ
Phương trình $\log_a x=b$ với $a$ dương khác 1 có nghiệm là $x=a^b$.
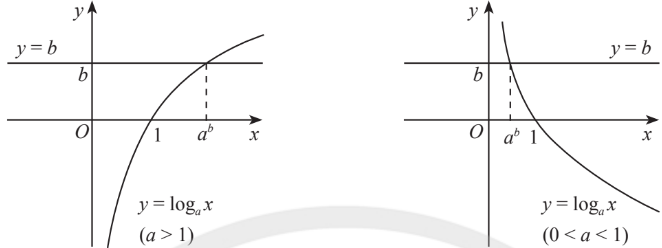
Bài tập:
Test16 | Phương trình logarit
Xét $a$ dương, khác 1
Dạng 1:
$a^x>b$
$a^x<b$
$a^x\geq b$
$a^x\leq b$

Vì $a^x$ luôn dương nên
- khi $b\leq 0$:
- $a^x<b$ vô nghiệm
- $a^x\leq b$ vô nghiệm
- $a^x>b$ có nghiệm $x\in R$ tùy ý
- $a^x\geq b$ có nghiệm $x\in R$ tùy ý
- khi $b>0$:
- **nếu $a>1$:
- $a^x<b$ có nghiệm $x<\log_a b$
- $a^x\leq b$ có nghiệm $x\leq\log_a b$
- $a^x>b$ có nghiệm $x>\log_a b$
- $a^x\geq b$ có nghiệm $x\geq\log_a b$
- **nếu $1>a>0$: dấu $>,<$ sẽ đảo chiều
- $a^x<b$ có nghiệm $x>\log_a b$
- $a^x\leq b$ có nghiệm $x\geq\log_a b$
- $a^x>b$ có nghiệm $x<\log_a b$
- $a^x\geq b$ có nghiệm $x\leq\log_a b$
- **nếu $a>1$:
Dạng 2:
$a^x>a^b$
- nếu $a>1$ thì $x>b$
- nếu $1>a>0$ thì $x<b$
Bài tập:
Test17 | Bất phương trình mũ
Xét $a$ dương, khác 1:
$\log_a x>b$

- Nếu $a>1$: nghiệm là
- $x>a^b$
- Nếu $1>a>0$: dấu $>$ sẽ đảo chiều
- $0<x<a^b$
Tương tự với các bất phương trình: $\log_a x<b, \log_a x\geq b, \log_a x\leq b$.
Bài tập:
Test18 | Bất phương trình logarit
Chương 7.
1. Đạo hàm

Đạo hàm tại $a$ của $f(x)$ là: $f'(a)=\underset{x\rightarrow a}{lim}\frac{f(x)-f(a)}{x-a}$.


2. Ý nghĩa hình học của đạo hàm


3. Số $e$


$\left ( x^n \right )’=n.x^{n-1}$
$(x)’=1$
$\left ( \sqrt{x} \right )’=\frac{1}{2\sqrt{x}}$

$\left ( \sin x \right )’=\cos x$
$\left ( \cos x \right )’=-\sin x$
$\left ( \tan x \right )’=\frac{1}{\cos^2 x}$
$\left ( \cot x \right )’=\frac{-1}{\sin^2 x}$
$\left ( e^x \right )’=e^x$
$\left ( a^x \right )’=a^x.\ln a$
$\left ( \ln x \right )’=\frac{1}{x}$
$\left ( \log_a x \right )’=\frac{1}{x.\ln a}$
$\left ( f(x)+g(x) \right )’=f'(x)+g'(x)$
$\left ( f(x)-g(x) \right )’=f'(x)-g'(x)$
$\left ( f(x).g(x) \right )’=f'(x).g(x)+f(x).g'(x)$
$\left ( \frac{f(x)}{g(x)} \right )’=\frac{f'(x).g(x)-f(x).g'(x)}{g(x)^2}$
$\left ( a.f(x) \right )’=a.f'(x)$ với $a$ là 1 con số
$\left ( \frac{1}{g(x)} \right )’=\frac{-g'(x)}{g(x)^2}$
Hàm hợp

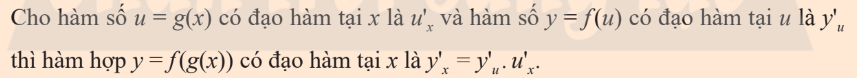

Đạo hàm cấp 2
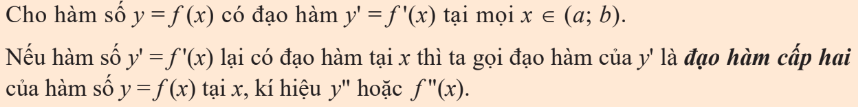

Đạo hàm cấp cao
Đạo hàm cấp 2: $f”(x)=\left ( f'(x) \right )’$
…………….cấp 3: $f^{(3)}(x)=\left ( f”(x) \right )’$
…………….cấp 4: $f^{(4)}(x)=\left ( f^{(3)}(x) \right )’$
Chương 8.
1. Góc giữa 2 đường thẳng
Kí hiệu góc giữa 2 đường thẳng: $(a,b)$
Cách xác định góc giữa 2 đường thẳng $a,b$:
- Tìm 2 đường thẳng $m,n$ song song hoặc trùng với $a,b$ sao cho $m,n$ cắt nhau.
- Lúc đó góc giữa $a,b$ bằng góc giữa $m,n$

2. Hai đường thẳng vuông góc
Hai đường thẳng vuông góc khi góc giữa chúng bằng $90^o$.

1. Đường thẳng vuông góc mặt phẳng
Đường thẳng $d$ vuông góc với mặt phẳng $(P)$ nếu: $d$ vuông góc tất cả các đường thẳng trên $(P)$.
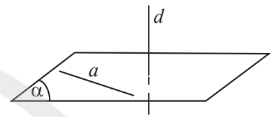
Đường thẳng $d$ vuông góc với mặt phẳng $(P)$ nếu:
- $d$ vuông góc với các đường thẳng $a,b$
- $a,b$ cắt nhau
- $a,b$ nằm trên $(P)$
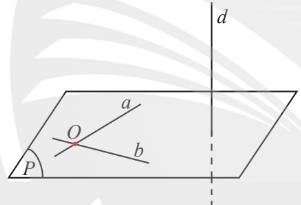

2. Song song và vuông góc

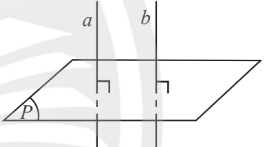

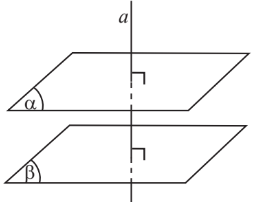

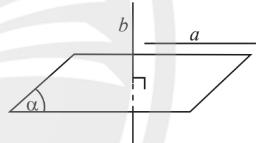
3. Phép chiếu vuông góc

Phép chiếu vuông góc: là phép chiếu như hình (c) bên dưới
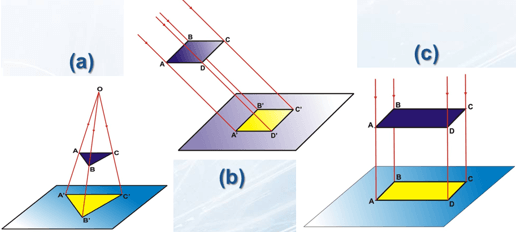

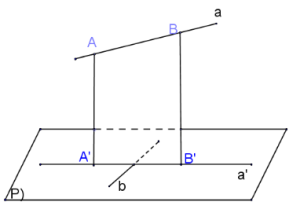
Định lý 3 đường vuông góc:
Qua phép chiếu vuông góc như hình dưới, nếu $b$ vuông $A’B’$ thì nó cũng vuông với $AB$ và ngược lại.
1. Góc giữa 2 mặt phẳng
Là góc giữa 2 đường thẳng vuông góc với 2 mặt phẳng đó.
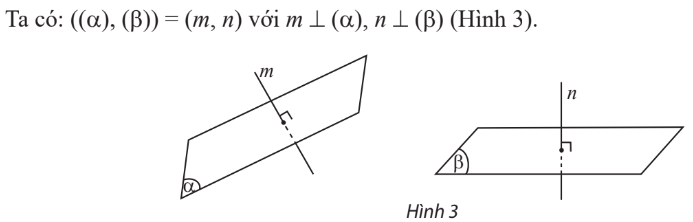

2. Hai mặt phẳng vuông góc
Hai mp vuông góc khi góc giữa chúng bằng $90^o$.

3. Tính chất cơ bản về 2 mặt phẳng vuông góc
Khi $(P)\perp (Q)$ với giao tuyến là $c$ thì nếu $a$ trên $(P)$ và $a\perp c$ thì $a\perp (Q)$.
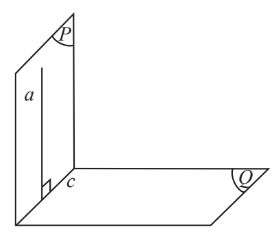
Nếu $(P),(Q)$ cùng vuông góc với $(R)$ và $d$ là giao tuyến của $(P),(Q)$ thì: $d\perp (R)$.
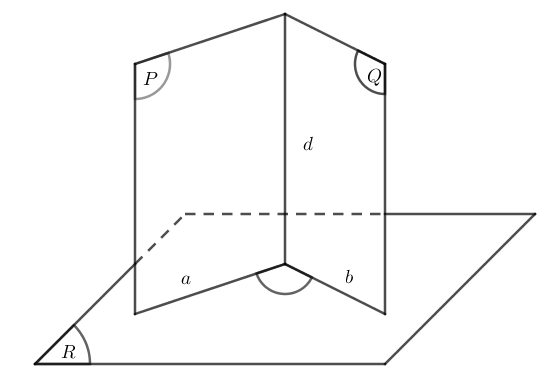
4. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

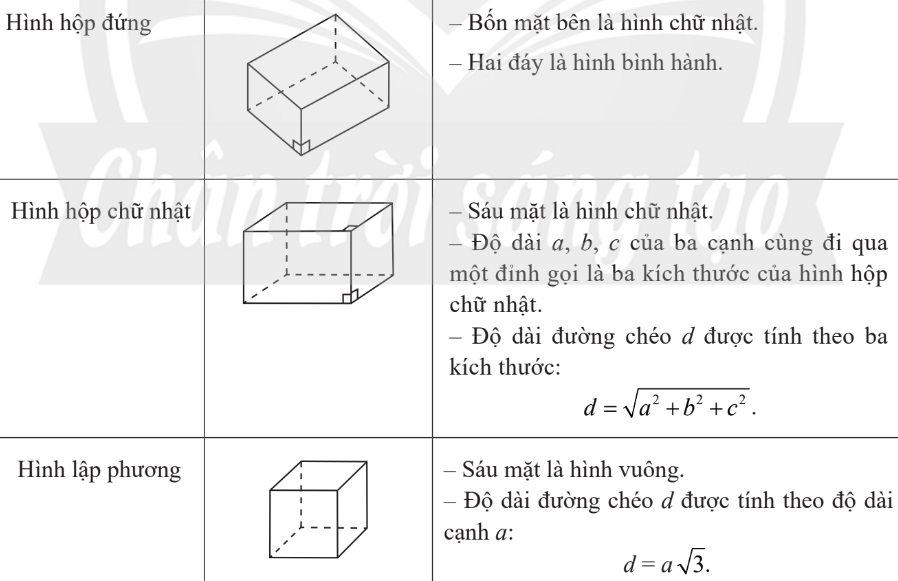

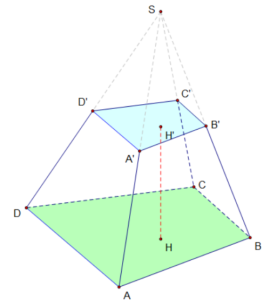
5. Hình chóp đều, hình chóp cụt đều

Hình chóp cụt: là phần hình chóp bị cắt (mất phần gần đỉnh) bởi 1 mặt phẳng song song với đáy.


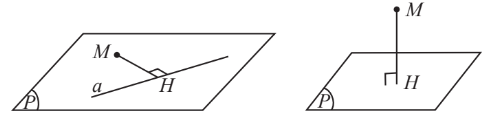
1. Khoảng cách từ 1 điểm đến 1 đường thẳng, đến 1 mặt phẳng
- là độ dài đường đi ngắn nhất
- kí hiệu: $d(… , … )$

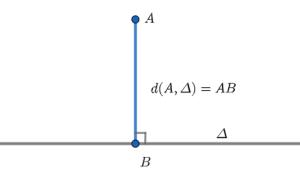
Khoảng cách giữa 2 điểm:

Khoảng cách từ 1 điểm đến 1 đường thẳng:
Khoảng cách từ 1 điểm đến 1 mặt phẳng:
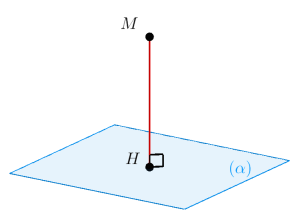
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song

Khoảng cách giữa 2 đường song song:

Khoảng cách giữa đường thẳng và mặt phẳng (song song nhau):
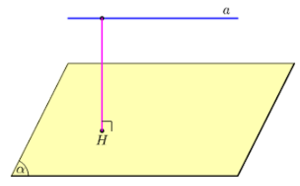
Khoảng cách giữa 2 mặt phẳng (song song nhau):
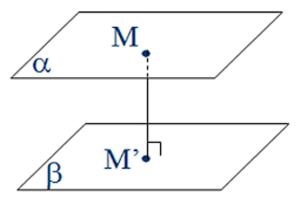
3. Khoảng cách giữa 2 đường chéo nhau


4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp
Thể tích khối hộp chữ nhật: $V=$ (dài) x (rộng) x (cao) = a.b.c
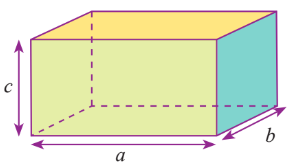
Thể tích khối chóp: $V=\frac{1}{3}$ x (Diện tích đáy) x (Chiều cao) = $\frac{1}{3}.S.h$
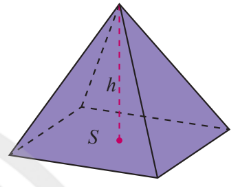
Thể tích khối chóp cụt đều: $V= \frac{1}{3}h(S+S’+\sqrt{S.S’})$
với $h$ là chiều cao và diện tích 2 đáy là $S$ và $S’$.
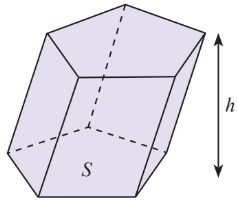
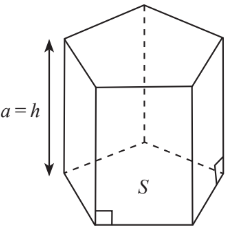
Thể tích khối lăng trụ: $V= (Diện tích đáy) x (Chiều cao) = S.h

1. Góc giữa đường thẳng và mặt phẳng:

2. Góc nhị diện và góc phẳng nhị diện

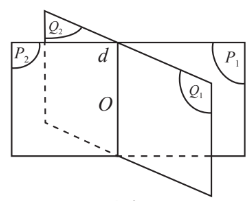

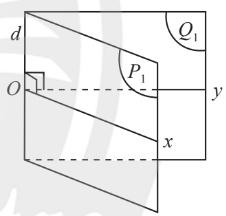
Góc nhị diện: tạo bởi 2 nửa mặt phẳng.
Kí hiệu: $[\alpha ,d,\beta ]$ với $d$ là đường giao tuyến.
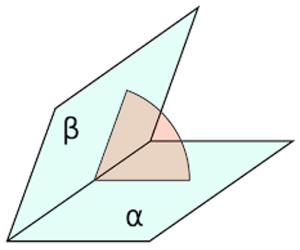
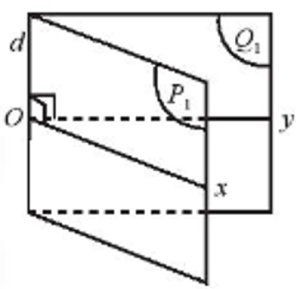
Góc phẳng nhị diện: là góc tạo bởi 2 đường trên 2 mặt phẳng sao cho chúng cùng vuông góc với đường giao tuyến
Chương 9.
1. Biến cố giao
Biến cố giao của $A$ và $B$ ý nghĩa là: cả $A$ và $B$ cùng xảy ra. Kí hiệu là: $AB$ hoặc $A\cap B$.
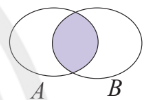
2. Hai biến cố xung khắc
Hai biến cố xung khắc: ko đồng thời xảy ra -> $A\cap B=\emptyset$.
3. Biến cố độc lập
Hai biến cố độc lập: $A$ xảy ra ko ảnh hưởng đến xác suất xảy ra của $B$.
![]()
4. Quy tắc nhân xác suất của 2 biến cố độc lập
Nếu $A$ và $B$ độc lập thì:
$P(AB)=P(A).P(B)$

1. Biến cố hợp
Biến cố hợp của $A$ và $B$ ý nghĩa là: $A$ hoặc $B$ xảy ra. Kí hiệu là: $A\cup B$.
2. Quy tắc cộng xác suất
Hai biến cố xung khắc: ko đồng thời xảy ra.
Quy tắc cộng 2 biến cố xung khắc
Nếu $A$ và $B$ xung khắc thì:
- $P(A\cup B)=P(A)+P(B)$
- $A\cap B=\emptyset$
Quy tắc cộng 2 biến cố bất kỳ:
$P(A\cup B)=P(A)+P(B)-P(AB)$