Toán 6 | Cơ bản
Chương 1.
Tập hợp
Tập hợp: gồm 1 nhóm đối tượng. Mỗi đối tượng được gọi là 1 phần tử.
Các tập hợp thường được kí hiệu bằng các chữ cái in hoa: $A,B,C,…$
Các phần tử của tập hợp thường được kí hiệu bằng các chữ cái in thường: $a,b,c,…$
Các phần tử của tập hợp được viết trong 2 dấu ngoặc nhọn “{}”, cách nhau bởi dấu “;”.
Để chỉ $a$ là 1 phần tử của tập hợp A, ta viết $a\in A$, đọc là $a$ thuộc $A$.
Ngược lại, $a$ không phải là 1 phần tử của $A$, ta viết $a\notin A$, đọc là $a$ không thuộc $A$.
Tập hợp rỗng: là tập hợp không chứa phần tử nào, kí hiệu là $\emptyset$.
Cách xác định tập hợp
Cách liệt kê các phần tử:
$A=\{0;2;4;6;8;10\}$.
Cách chỉ ra tính chất đặc trưng:
$A=\{ x|x \text{ là số tự nhiên chẵn và } x<12 \}$.
Các phần tử có thể viết theo thứ tự tùy ý:
$A=\{0;2;4;6;8;10\}=\{8;10;4;6;2;0\}$.
Các phần tử chỉ liệt kê 1 lần:
Tập hợp các chữ cái trong từ “beginning” là $B=\{b;e;g;i;n\}$.
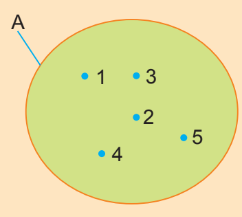
Biểu đồ Ven:
$A=\{1;2;3;4;5\}$
Tập hợp $\mathbb{N}$ và $\mathbb{N}^*$
$\mathbb{N}=\{0;1;2;3;4;5;…\}$
$\mathbb{N}^*=\{1;2;3;4;5;…\}$
Thứ tự trong tập hợp số tự nhiên
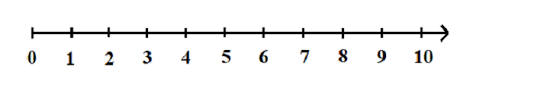
Số $a$ nhỏ hơn số $b$ kí hiệu là $a<b$. Khi đó, trên trục số, $a$ nằm bên trái $b$.
Số $b$ lớn hơn số $a$ kí hiệu là $b>a$. Khi đó, trên trục số, $b$ nằm bên phải $a$.
Ta viết $a\leq b$ để chỉ $a<b$ hoặc $a=b$.
Ta viết $c\geq d$ để chỉ $c>d$ hoặc $c=d$.
Số liền sau của một số: là số nằm bên phải số đó, và lớn hơn nó 1 đơn vị.
Số liền trước của một số: là số nằm bên trái số đó, và nhỏ hơn nó 1 đơn vị.
Tính chất bắc cầu: nếu $a<b$ và $b<c$ thì $a<c$.
Ghi số tự nhiên
Hệ thập phân
Cấu tạo thập phân của 1 số:
Số có 2 chữ số: $\overline{ab}=a\times 10+b$.
Số có 3 chữ số: $\overline{abc}=a\times 100+b\times 10+c$.
Ví dụ: $26=2\times 10+6$
$378=3\times 100+7\times 10+8$
Hệ La Mã

Thêm “I” vào bên trái “V” là giảm giá trị:
IV $=5-1=4$.
Thêm “I” vào bên phải “V” là tăng giá trị:
VI $=5+1=6$.
Tương tự với “X”.


Phép cộng và phép nhân
$a+b=c$.
$a,b$ là các số hạng.
$c$ là tổng.
$m\times n=p$.
$m,n$ là các thừa số.
$p$ là tích.
Có thể thay dấu “$\times $” bằng dấu “.”
$m\times n==m.n=p$.
Ví dụ: $2+3=5$.
2 và 3 là các số hạng, 5 là tổng.
$4\times 6=4.6=24$.
4 và 6 là các thừa số, 24 là tích.
Tính chất của phép cộng và phép nhân
Giao hoán:
$a+b=b+a$
$a.b=b.a$
Tính chất kết hợp:
$(a+b)+c=a+(b+c)$
$(a.b).c=a.(b.c)$
Tính chất phân phối:
$a.(b+c)=a.b+a.c$
Tính chất của 0 và 1:
$a+0=a$
$a.1=a$
Phép trừ và phép chia hết
Phép trừ
Cho $a\geq b$.
$a-b=c$.
$a$ là số bị trừ.
$b$ là số trừ.
$c$ là hiệu.
Phép chia
$m:n=p$.
$m$ là số bị chia.
$n$ là số chia.
$p$ là thương.
Tính chất phân phối:
$a.(b-c)=a.b-a.c$.
Tính chất của số 1:
$a:1=a$
Lũy thừa
Lũy thừa bậc $n$ của $a$, kí hiệu $a^n$, là tích của $n$ thừa số $a$.
$a^n=\underbrace{a.a. … .a}_{n\text{ thừa số } a}$.
($n\neq 0$).
$a^n$ đọc là $a$ mũ $n$, hoặc $a$ lũy thừa $n$, hoặc lũy thừa bậc $n$ của $a$.
$a^2$ đọc là $a$ mũ 2, hoặc $a$ lũy thừa 2, hoặc $a$ bình phương, hoặc bình phương của $a$.
$a^3$ đọc là $a$ mũ 3, hoặc $a$ lũy thừa 3, hoặc $a$ lập phương, hoặc lập phương của $a$.
Quy ước: $a^1=a$.
$a^0=1$ với $a\neq 0$.
Nhân 2 lũy thừa
$a^m.a^n=a^{m+n}$.
$5^2.5^7=5^9$.
Chia 2 lũy thừa
$a^m:a^n=a^{m-n}$.
Thứ tự thực hiện phép tính
- từ trái sang phải
- phép tính trong cặp dấu ngoặc “(,)” trong cùng
- phép lũy thừa
- phép nhân, chia
- phép cộng, trừ
Chia hết và chia có dư
Cho 2 số tự nhiên $a,b$ với $b$ khác 0.
Luôn có thể biểu diễn kiểu: $a=b.q+r$ với $0\leq r<b$, tức là $a:b=q$ dư $r$.
$a$ là số bị chia, $b$ là số chia, $q$ là thương, $r$ là số dư.
Nếu $r=0$ thì $a:b=q$, ta nói $a$ chia hết cho $b$, kí hiệu $a\vdots b$, lúc đó ta gọi là phép chia hết.
Nếu $r\neq 0$ thì $a:b=q$ dư $r$, ta nói $a$ không chia hết cho $b$, kí hiệu $a\not\vdots b$, lúc đó ta gọi là phép chia có dư.
Tính chất chia hết
Nếu $a,b\vdots n$ thì $a+b\vdots n$ và $a-b\vdots n$.
Nếu $a\vdots n,b\not\vdots n$ thì $a+b\not\vdots n$ và $a-b\not\vdots n$.
Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng bên phải là “0;2;4;6;8” thì chia hết cho 2.
Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng bên phải là “0;5” thì chia hết cho 5.
Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
Ước và bội
$a$ chia hết cho $b$ thì $a$ là bội của $b$, và $b$ là ước của $a$.
Tập hợp các ước của số $n$ là Ư($n$).
Tập hợp các bội của số $n$ là B($n$).
4 chia hết cho các số 1;2;4 nên Ư(4) = {1; 2; 4}.
Các bội của 4 là 0; 4; 8; 12;… nên B(4) = {0; 4; 8; 12; …}.
Số 0 là bội của mọi số tự nhiên.
Số 1 là ước của mọi số tự nhiên.
Mọi số tự nhiên $n$ đều có 2 ước là 1 và chính nó.
Ư($n$) = {1; …; $n$}.
Cách tìm ước
Chia lần lượt số $a$ cho các số nhỏ hơn, nếu chia hết cho số nào thì số đó là ước của $a$.
Cách tìm bội
Nhân lần lượt số $n$ với 0; 1; 2; 3; … ta sẽ được các bội của số $n$.
B($n$) = {$0;n;2n;3n;4n;…$}.
Số nguyên tố. Hợp số
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó.
Hợp số là số tự nhiên lớn hơn 1 và có nhiều hơn 2 ước.
Các số nguyên tố là: $2;3;5;7;11;13;…$.
Các hợp số là: $4;6;8;9;10;12;14;…$
Phân tích một số ra thừa số nguyên tố
Phân tích một số ra thừa số nguyên tố là viết số đó dưới dạng tích của các thừa số nguyên tố.
Cách phân tích một số ra thừa số nguyên tố
Cách 1: theo cột dọc
Chia lần lượt cho các ước là số nguyên tố của nó đến khi kết quả cuối cùng bằng 1. Chia ước nhỏ trước.
Ví dụ: phân tích số 280.
Chia cho các số nguyên tố: $2;3;5;7;11;…$.
Chia 2 trước: 280:2 = 140. Viết số 2 bên phải, số 140 bên trái, dưới số 280.
Lấy 140 chia 2 tiếp: 140:2=70.
Lại lấy 70 chia 2 được 35.
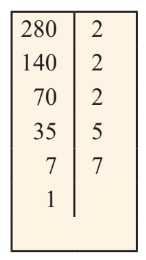
35 không chia 2 được, cũng không chia 3 được, nên chia 5. Ta có 35:5=7.
7 không chia 5 được, chia tiếp cho 7.
7:7=1. Kết quả là 1 nên dừng lại.
Các số bên phải là các số cần tìm.
$280=2.2.2.5.7=2^3.5.7$
Cách 2: theo sơ đồ cây
Chia lần lượt cho các ước của nó đến khi kết quả cuối cùng bằng 1. Không cần chia các ước nhỏ trước.
Bên dưới là 3 cách phân tích khác nhau ở giai đoạn đầu.
Cách bên trái chia lần lượt cho 2.
Cách ở giữa chia 3 trước, rồi chia 2, và rồi chia 2 tiếp.
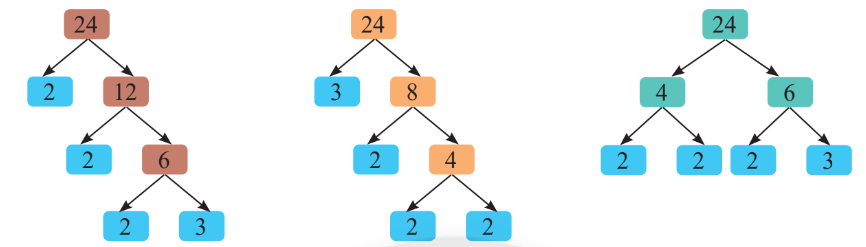
Cách bên phải chia 4 trước, các kết quả nhận được lại mang đi chia cho 2.
Kết quả nhận được đều như nhau: $24=2.2.2.3=2^3.3$.
Ước chung
$x$ là ước chung của $a,b$ nếu $a\vdots x$ và $b\vdots x$.
Tập hợp các ước chung của $a,b$ kí hiệu là ƯC($a,b$)
Cách tìm ước chung của $a,b$
Tìm Ư($a$), Ư($b$), rồi tìm các phần tử chung nhau của Ư($a$) và Ư($b$).
Ước chung lớn nhất
Là số lớn nhất trong tập hợp các ước chung.
Ước chung lớn nhất của $a,b$ kí hiệu là ƯCLN($a,b$).
Tìm ước chung lớn nhất bằng cách phân tích ra thừa số nguyên tố
- Phân tích mỗi số ra thừa số nguyên tố
- Chọn ra các thừa số nguyên tố chung
- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
Ví dụ: $54=2.3^3$
$90=2.3^2.5$
Các thừa số nguyên tố chung là 2 và 3. Giữa $3^3$ và $3^2$ thì chọn $3^2$ vì có số mũ nhỏ hơn.
Vậy ƯCLN$(54,90) = 2.3^2=18$.
Hai số có ƯCLN bằng 1 gọi là 2 số nguyên tố cùng nhau.
Ứng dụng trong rút gọn phân số
Rút gọn để được phân số tối giản:
Cách 1: chia dần tử và mẫu cho ước chung của chúng đến khi không thể chia được nữa.
$\frac{90}{126}=\frac{45}{63}=\frac{15}{21}=\frac{5}{7}$.
Đầu tiên chia 2, rồi chia 3, rồi chia 3 tiếp.
Cách 2: chia 1 lần cho ƯCLN.
$\frac{90}{126}=\frac{90:18}{126:18}==\frac{5}{7}$.
Bội chung
$x$ là bội chung của $a,b$ nếu $x$ là bội của cả $a$ và $b$.
Tập hợp các bội chung của $a,b$ kí hiệu là BC($a,b$)
Cách tìm bội chung của $a,b$
Tìm B($a$), B($b$), rồi tìm các phần tử chung nhau của B($a$) và B($b$).
Bội chung nhỏ nhất
Là số nhỏ nhất khác 0 trong tập hợp các bội chung.
Bội chung nhỏ nhất của $a,b$ kí hiệu là BCNN($a,b$).
Tìm bội chung nhỏ nhất bằng cách phân tích ra thừa số nguyên tố
- Phân tích mỗi số ra thừa số nguyên tố
- Chọn ra các thừa số nguyên tố chung và riêng
- Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ví dụ: $12=2^2.3$
$90=2.3^2.5$
$750=2.3.5^3$
Các thừa số nguyên tố là 2, 3, 5, chọn với số mũ lớn nhất là $2^2,3^2,5^3$.
Vậy BCNN(12, 90, 750) = $2^2.3^2.5^3=4500$.
Ứng dụng trong quy đồng mẫu số
Quy đồng mẫu số:
Cách 1: nhân 2 mẫu số
$\frac{1}{200}+\frac{4}{300}=\frac{1.300+4.200}{200.300}=\frac{1100}{60000}$.
Cách 2: lấy mẫu số chung là BCNN của 2 mẫu số
$\frac{1}{200}+\frac{4}{300}=\frac{1.3+4.2}{600}=\frac{11}{600}$.
Chương 2.
Làm quen với số nguyên âm
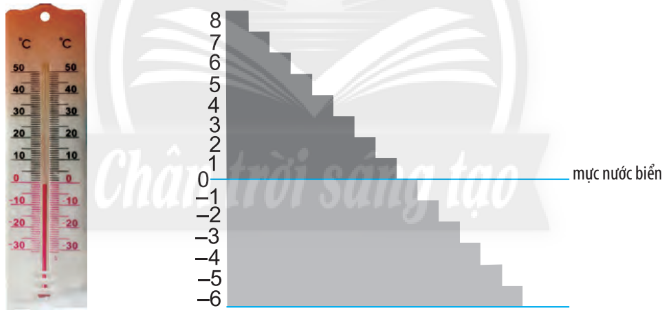
Số nguyên âm được ghi như sau: -1; -2;l -3; …, đọc là âm một, âm hai, âm ba,…, hoặc trừ một, trừ hai, trừ ba,…
Tập hợp số nguyên
Số nguyên dương: +1; +2; +3;…
Số nguyên dương có thể viết tắt bằng cách bỏ dấu “+” thành: 1; 2; 3;…
Số nguyên âm: -1; -2; -3;…
Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.
Tập hợp số nguyên: gồm số nguyên âm, số nguyên dương, và số 0.
Số đối của một số nguyên

Hai số đối nhau: là 2 số ở 2 bên và cách đều vị trí số 0.
6 là số đối của -6.
-5 là số đối của 5.
1 là số đối của -1.
0 là số đối của 0.
So sánh 2 số nguyên

Trên trục số, nếu $a$ nằm bên trái $b$ thì $a$ nhỏ hơn $b$ kí hiệu $a<b$, hoặc $b>a$.
Thứ tự trong tập hợp số nguyên
Săp xếp các số $-5;4;-2;;0;2$ theo thứ tự tăng dần:
$-5;-2;0;2;4$
Cộng 2 số nguyên cùng dấu


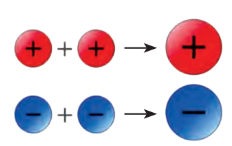
$(+a)+(+b)=+(a+b)$
$(-a)+(-b)=-(a+b)$
$(+2)+(+3)=+(2+3)=+5=5$
$(-2)+(-3)=-(2+3)=-5$
$2+3=5$
Cộng 2 số nguyên khác dấu
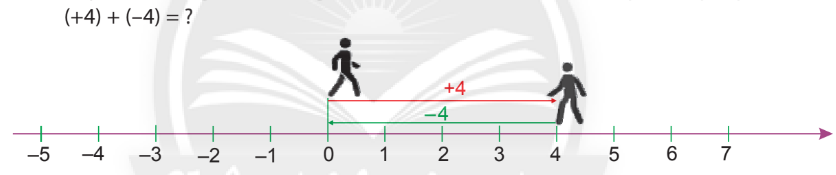
Khi 2 số giống nhau:
$(+a)+(-a)=0$
$a+(-a)=a$

Khi $a<b$:
$(-a)+(+b)=b-a$
$(-2)+(+6)=6-2=4$
$(+a)+(-b)=-(b-a)$
$(+2)+(-6)=-(6-2)=-4$
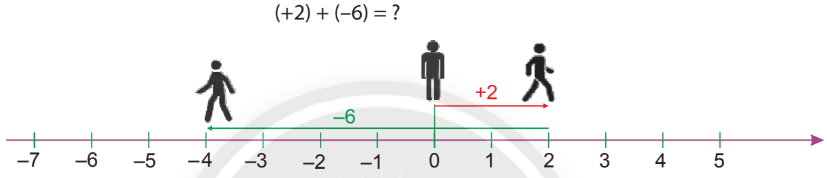
Khi $a>b$:
$(-a)+(+b)=-(a-b)$
$(-5)+(+2)=-(5-2)=-3$
$(+a)+(-b)=a-b$
$(+5)+(-2)=5-2=3$
Số nào lớn thì kết quả ra dấu của số đó.
Tính chất của phép cộng các số nguyên
Giao hoán:
$a+b=b+a$
$(-2)+3=3+(-2)$
$a+0=0+a=a$
Kết hợp:
$(a+b)+c=a+(b+c)$
$2+3+(-3)=(2+3)+(-3)=5+(-3)=2$
$2+3+(-3)=2+(3+(-3))=2+0=2$
Phép trừ 2 số nguyên
$-(-a)=a$
$a-b=a+(-b)$
$1-2=1+(-2)=-(2-1)=-1$
$1-(-2)=1+2=3$
$(-2)-3=(-2)+(-3)=-(2+3)=-5$
$(-2)-(-3)=(-2)+3=3-2=1$
Quy tắc dấu ngoặc
Dấu “+” trước “(,)” thì khi bỏ “(,)” thì các số hạng trong “(,)” giữ nguyên dấu
$a+(b+c-d)=a+b+c-d$
$a+(-b-c+d)=a-b-c+d$
Dấu “-” trước “(,)” thì khi bỏ “(,)” thì các số hạng trong “(,)” đổi dấu
$a-(b+c-d)=a-b-c+d$
$a-(-b-c+d)=a+b+c-d$
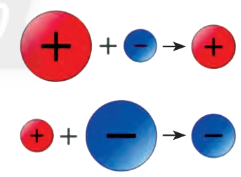
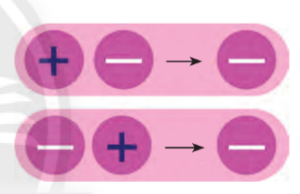
Nhân 2 số nguyên khác dấu
$(+a).(-b)=-a.b$
$(-a).(+b)=-a.b$
Nhân 2 số nguyên cùng dấu
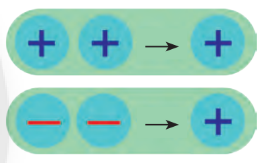
$(+a).(+b)=a.b$
$(-a).(-b)=a.b$
Tính chất của phép nhân
Giao hoán: $a.b=b.a$
Kết hợp: $(a.b).c=a.(b.c)$
Phân phối:
$a.(b+c)=a.b+a.c$
$a.(b-c)=a.b-a.c$
$a.(-b+c)=-a.b+a.c$
Phép chia hết
Cho 2 số nguyên $a,b$ với $b$ khác 0.
Nếu có số nguyên $q$ sao cho $a=b.q$ thì ta nói $a$ chia hết cho $b$, kí hiệu $a\vdots b$, $q$ là thương của phép chia. Khi đó, ta có $a:b=q$.
Bội và ước của số nguyên
Nếu $a\vdots b$ thì $b$ là ước của $a$, và $a$ là bội của $b$.
Các ước tự nhiên của 12 là: $1;2;3;4;6;12$.
Các ước nguyên của 12 là: $1;2;3;4;6;12;-1;-2;-3;-4;-6;-12$.
Các bội tự nhiên của 3 là: $0;3;6;9;…$
Các bội nguyên của 3 là: $0;3;6;9;…;-3;-6;-9;…$
Chương 3.
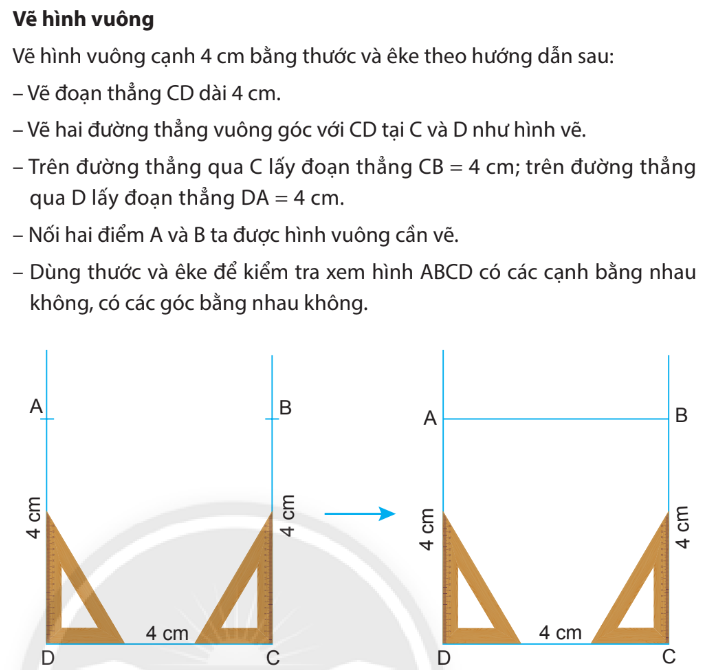
Hình vuông

2 đường chéo của hình vuông thì bằng nhau.
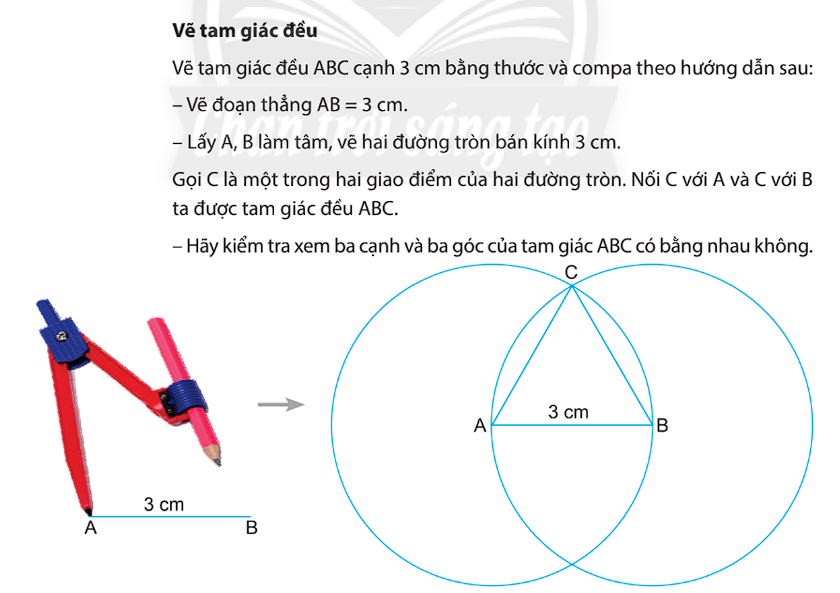
Tam giác đều

Lục giác đều

3 đường chéo chính của lục giác đều thì bằng nhau.
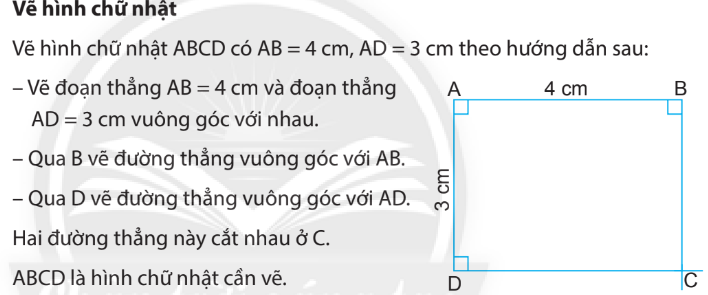
Hình chữ nhật

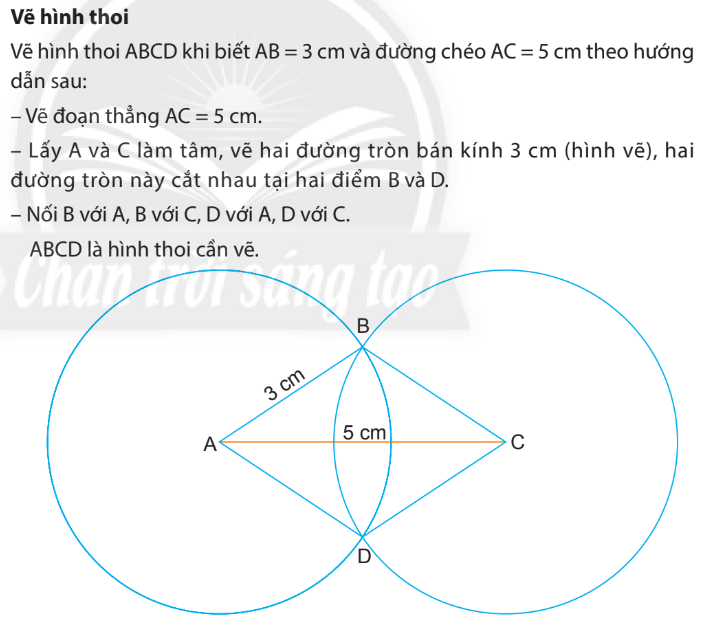
Hình thoi

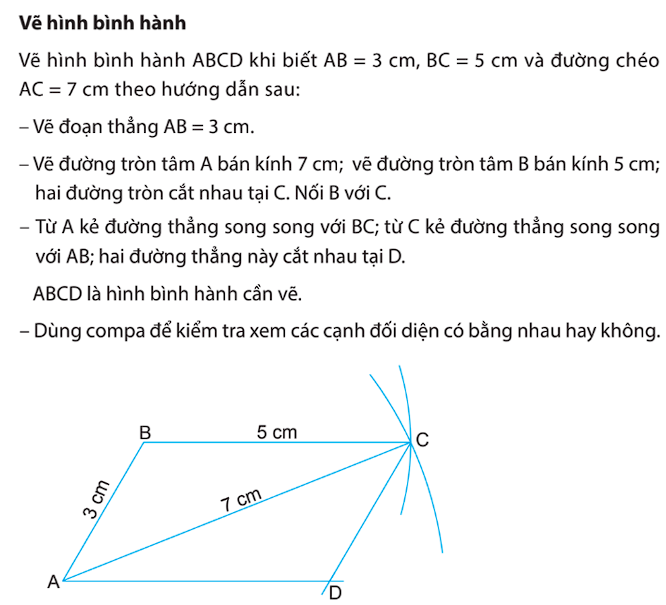
Hình bình hành

Hình thang cân
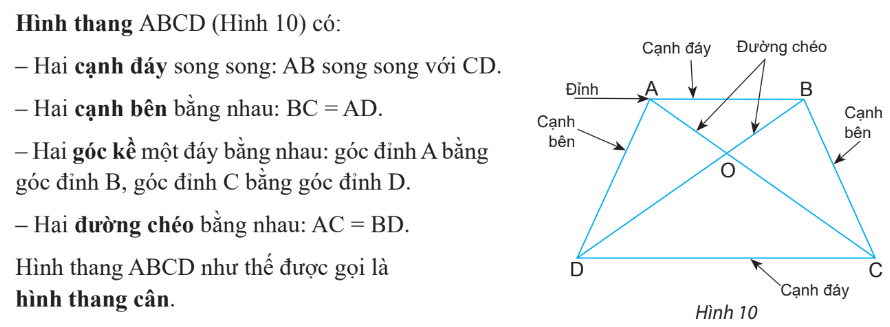
Chu vi và diện tích của một số hình đã học

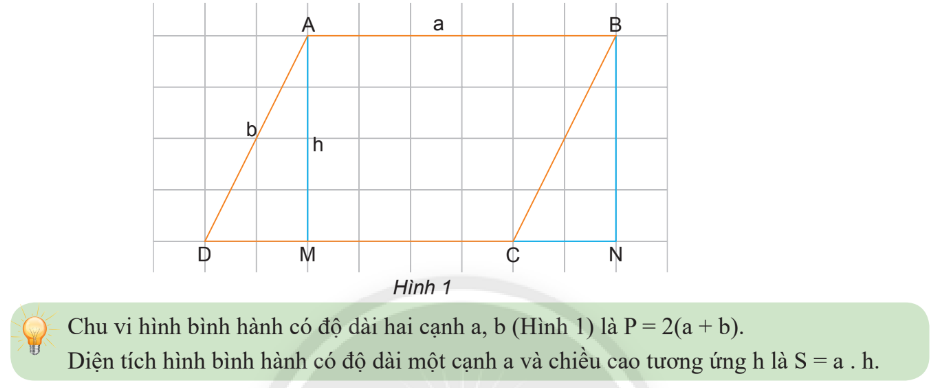
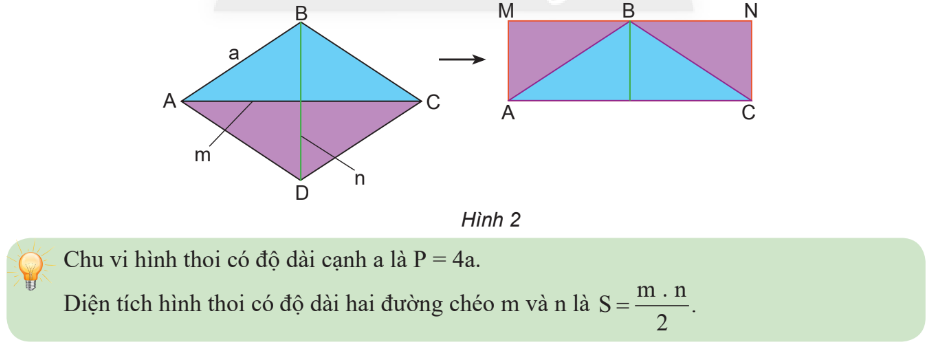
Chu vi và diện tích của hình bình hành, hình thoi
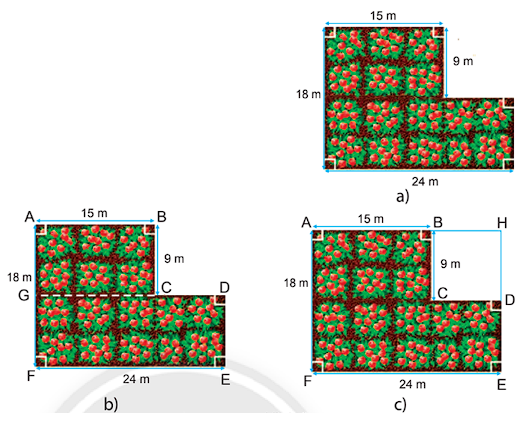
Chu vi và diện tích của một số hình trong thực tiễn
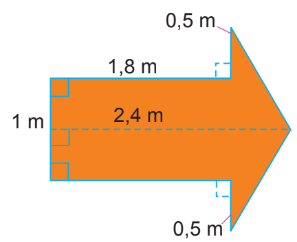
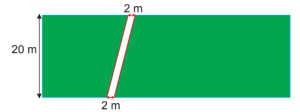
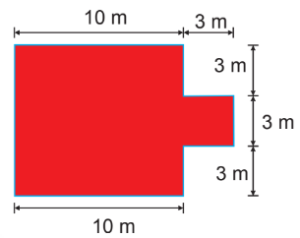
Chương 4.
Thu thập dữ liệu
Dữ liệu: là các thông tin thu thập được như số, chữ, hình ảnh,…
Số liệu: dữ liệu dạng số.
Phân loại dữ liệu
Là việc sắp xếp thông tin theo những tiêu chí nhất định.
Tính hợp lí của dữ liệu
Các tiêu chí đánh giá:
- đúng định dạng
- nằm trong phạm vi dự kiến
Bảng dữ liệu ban đầu
Là dữ liệu được thu thập và ghi lại.
Bảng thống kê
Là 1 cách trình bày dữ liệu khác so với bảng dữ liệu ban đầu, gồm các hàng và các cột, thể hiện danh sách các đối tượng thống kê cùng với các dữ liệu của đối tượng đó.
Biểu đồ trang
Sử dụng biểu tượng hoặc hình ảnh để thể hiện dữ liệu.
Một hình ảnh có thể thay thế nhiều đối tượng.
Biểu đồ tranh trực quan, dễ hiểu.


Đọc biểu đồ tranh
Cần xác định 1 hình ảnh thay thế bao nhiêu đối tượng.
Từ số lượng hình ảnh ta sẽ có số đối tượng tương ứng.
Vẽ biểu đồ tranh

Biểu đồ cột
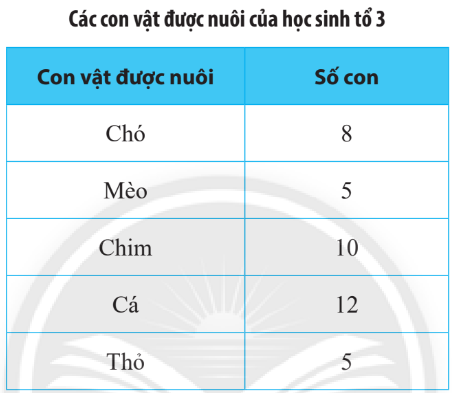
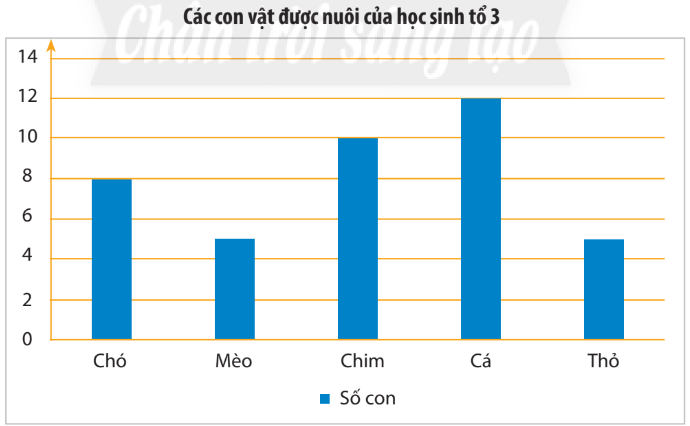
Đọc biểu đồ cột
- Nhìn theo 1 trục để đọc danh sách các đối tượng thống kê.
- Nhìn theo trục còn lại để đọc số liệu thống kê tương ứng với các đối tượng đó.
Vẽ biểu đồ cột

Biểu đồ cột kép
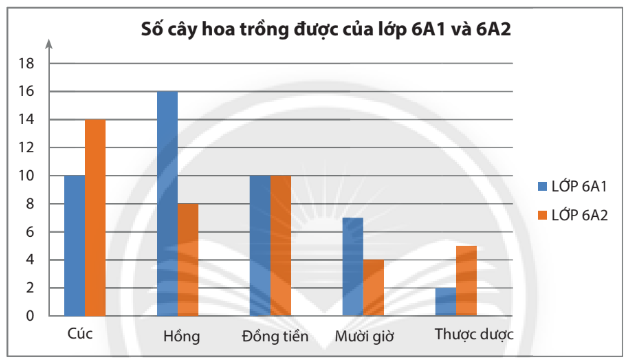
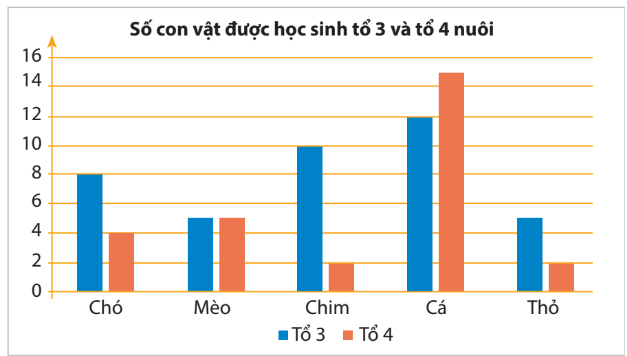
Đọc biểu đồ cột kép
Tương tự cách đọc biểu đồ cột.
Vẽ biểu đồ cột kép
Tương tự cách vẽ biểu đồ cột.
Chương 5.
Mở rộng khái niệm phân số
$\frac{a}{b}$: đọc là $a$ phần $b$.
Ta gọi $\frac{a}{b}$ là phân số, với $a,b\in\mathbb{Z},b$ khác 0, $a$ là tử số, $b$ là mẫu số.
Phân số bằng nhau
$\frac{a}{b}$ và $\frac{c}{d}$ được gọi là bằng nhau nếu $a.d=b.c$, kí hiệu là $\frac{a}{b}=\frac{c}{d}$.
Biểu diễn số nguyên ở dạng phân số
Mỗi số nguyên $n$ có thể coi là phân số $\frac{n}{1}$, ta viết $\frac{n}{1}=n$.
Tính chất 1
$\frac{a}{b}=\frac{a.c}{b.c}$ với $c$ khác 0.
Tính chất 2
$\frac{a}{b}=\frac{a:c}{b:c}$ với $c$ khác 0.
$\frac{a}{-b}=\frac{-a}{b}$.
So sánh 2 phân số có cùng mẫu
Khi mẫu số dương:
Nếu có $a<c$ và $b>0$ thì $\frac{a}{b}<\frac{c}{b}$
\frac{-3}{4}<\frac{1}{4}
Khi mẫu số âm:
Chuyển sang dạng có mẫu dương rồi so sánh.
$\frac{a}{-b}=\frac{-a}{b}$
So sánh $\frac{3}{-4}$ và $\frac{-7}{-4}$.
$\frac{3}{-4}=\frac{-3}{4}$
$\frac{-7}{-4}=\frac{7}{4}$
$\frac{-3}{4} < \frac{7}{4}$ nên $\frac{3}{-4}<\frac{-7}{-4}$.
So sánh 2 phân số có khác mẫu
Quy đồng để có cùng mẫu số dương rồi so sánh.
So sánh $\frac{3}{-4}$ và $\frac{-5}{6}$.
$\frac{3}{-4}=\frac{-3}{4}=\frac{-3.6}{4.6}=\frac{-18}{24}$
$\frac{-5}{6}=\frac{-5.4}{6.4}=\frac{-20}{24}$
$\frac{-18}{24} >\frac{-20}{24}$ nên $\frac{3}{-4}>\frac{-5}{6}$.
So sánh phân số với số nguyên
So sánh 2 và $\frac{7}{3}$.
$2=\frac{2}{1}=\frac{2.3}{1.3}=\frac{6}{3}$
$\frac{6}{3}<\frac{7}{3}$ nên $2<\frac{7}{3}$.
So sánh -3 và $\frac{7}{-2}$.
$\frac{7}{-2}=\frac{-7}{2}$
$-3=\frac{-3}{1}=\frac{-3.2}{1.2}=\frac{-6}{2}$
$\frac{-6}{2}>\frac{-7}{2}$ nên $-3>\frac{7}{-2}$.
Tính chất bắc cầu
Nếu có $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{m}{n}$ thì $\frac{a}{b}<\frac{m}{n}$.
Phép cộng 2 phân số
Cùng mẫu: chỉ cần cộng tử số và giữ nguyên mẫu số
$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$
\frac{2}{3}+\frac{5}{3}=\frac{2+5}{3}=\frac{7}{3}
Khác mẫu: quy đồng mẫu rồi cộng
$\frac{a}{b}+\frac{c}{d}=\frac{a.d+b.c}{b.d}$
$\frac{2}{3}+\frac{4}{5}=\frac{2.5+3.4}{3.5}=\frac{22}{15}$
Tính chất của phép cộng phân số
Giao hoán:
$\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$
Kết hợp:
$\frac{a}{b}+\left (\frac{c}{d}+\frac{m}{n} \right )=\left (\frac{a}{b}+\frac{c}{d} \right )+\frac{m}{n}$
Số đối
Số đối của $\frac{a}{b}$ là $-\frac{a}{b}=\frac{-a}{b}=\frac{a}{-b}$.
Ta có $\frac{a}{b}+\left ( -\frac{a}{b} \right )=0$.
Phép trừ 2 phân số
$\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left (-\frac{c}{d} \right )$.
Quy tắc dấu ngoặc
Dấu “+” trước “(,)” thì khi bỏ “(,)” thì các số hạng trong “(,)” giữ nguyên dấu
$\frac{a}{b}+(\frac{c}{d}+\frac{g}{h}-\frac{s}{t})=\frac{a}{b}+\frac{c}{d}+\frac{g}{h}-\frac{s}{t}$.
$\frac{a}{b}+(-\frac{c}{d}-\frac{g}{h}+\frac{s}{t})=\frac{a}{b}-\frac{c}{d}-\frac{g}{h}+\frac{s}{t}$.
Dấu “-” trước “(,)” thì khi bỏ “(,)” thì các số hạng trong “(,)” đổi dấu
$\frac{a}{b}-(\frac{c}{d}+\frac{g}{h}-\frac{s}{t})=\frac{a}{b}-\frac{c}{d}-\frac{g}{h}+\frac{s}{t}$.
Nhân 2 phân số
$\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$.
Tính chất của phép nhân phân số
Giao hoán:
$\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{a}{b}$
Kết hợp:
$\frac{a}{b}.\left (\frac{c}{d}.\frac{m}{n} \right )=\left (\frac{a}{b}.\frac{c}{d} \right ).\frac{m}{n}$
Phân phối:
$\frac{a}{b}.\left (\frac{c}{d}+\frac{m}{n} \right )=\frac{a}{b}.\frac{c}{d} +\frac{a}{b}.\frac{m}{n}$
$\frac{a}{b}.\left (\frac{c}{d}-\frac{m}{n} \right )=\frac{a}{b}.\frac{c}{d} -\frac{a}{b}.\frac{m}{n}$
Chia phân số
$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}$.
Tính giá trị phân số của 1 số
Giá trị $\frac{1}{2}$ của $12$ là $\frac{1}{2}.12=6$.
Giá trị $\frac{3}{2}$ của $12$ là $\frac{3}{2}.12=18$ (để ý $18=6.3$).
Giá trị $\frac{1}{n}$ của $12$ là $\frac{1}{n}.12$.
Giá trị $\frac{m}{n}$ của $12$ là $\frac{m}{n}.12$.
Giá trị $\frac{m}{n}$ của $a$ là $\frac{m}{n}.a$.
Tìm 1 số khi biết giá trị phân số của nó
Nếu giá trị $\frac{1}{2}$ của $x$ là $8$ thì $\frac{1}{2}.x=8$. Nên $x=8:\frac{1}{2}=16$.
Nếu giá trị $\frac{3}{2}$ của $y$ là $9$ thì $\frac{3}{2}.y=9$. Nên $y=9:\frac{3}{2}=6$.
Nếu giá trị $\frac{a}{b}$ của $z$ là $c$ thì $\frac{a}{b}.z=c$. Nên $z=c:\frac{a}{b}$.
Hỗn số
Nếu $a$ chia $b$ được thương là $c$, số dư là $d$ thì ta viết $\frac{a}{b}=c\frac{d}{b}$.
$c\frac{d}{b}$ gọi là hỗn số, đọc là “c, d phần b”.
Đổi hỗn số ra phân số
$c\frac{d}{b}=\frac{c.b+d}{d}$
Chương 6.
Số thập phân âm
Phân số thập phân là phân số có mẫu số là lũy thừa của 10.
$\frac{7}{10},\frac{-8}{100},\frac{9}{1000},\frac{-1013}{10000},…$
Dạng số thập phân của phân số thập phân:
Mẫu số là 10: bên phải dấu “,” có 1 chữ số
$\frac{9}{10}=0,9,\frac{71}{10}=7,1,\frac{-815}{10}=-81,5$
Mẫu số là 100: bên phải dấu “,” có 2 chữ số
$\frac{-6}{100}=-0,06,\frac{71}{100}=0,71,\frac{934}{100}=9,34$
Mẫu số là 1000: bên phải dấu “,” có 3 chữ số
$\frac{2}{1000}=0,002,\frac{-34}{1000}=-0,034,\frac{246}{1000}=0,246,\frac{-7890}{1000}=-7,890$
Số thập phân gồm 2 phần:
- phần số nguyên: bên trái dấu “,”
- phần thập phân: bên phải dấu “,”
Số $-12,345$ có phần số nguyên là $-12$, phần thập phân là $345$.
Số đối của 1 số thập phân
Số đối của $2,5$ là $-2,5$.
Số đối của $-0,0025$ là $0,0025$.
So sánh 2 số thập phân
$2,1>2,0$
$-1,05>-1,051$
Cộng, trừ 2 số thập phân
$5,1+6,2=11,3$
$(-3,4)+(-15,11)=-18,51$
$-5+4,2=-(5-4,2)=-0,8$
$-3+6,6=6,6-3=3,6$
$7,8-7,21=0,59$
$1-10,77=-(10,77-1)=-9,77$
Nhân, chia 2 số thập phân
Để tính: $12,345.6,78$.
Đầu tiên, bỏ dấu “,” và nhân như 2 số nguyên: $12345.678=8369910$.
Đếm số chữ số bên phải dấu “,” của từng thừa số: “,345” có 3 chữ số, “,78” có 2 chữ số. Vậy tổng cộng có 5 chữ số bên phải dấu “,”.
Ta sẽ đặt dấu phẩy vào tích sau cho có 5 chữ số bên phải dấu phẩy: $83,69910$.
Vậy $12,345.6,78=83,69910$.
Tính: $-0,3.0,05$.
Nhân 2 số nguyên: $-3.5=-15$
Bên phải dấu “,” của 2 thừa số có tổng cộng là 3 chữ số.
Do tích là $-15$ chỉ có 2 chữ số nên ta thêm số 0 vào bên trái cho đủ 3 chữ số bên phải dấu phẩy: $-0,015$.
Vậy $-0,3.0,05=-0,015$.
Tính chất của các phép tính với số thập phân
Giao hoán, kết hợp:
$0,5+1,7+0,5=0,5+0,5+1,7=2,7$.
$15,81+91-15,81=15,81+91+(-15,81)=15,81+(-15,81)+91=91$.
Phân phối:
$15.0,7+15.0,3=15.(0,7+0,3)=15$.
$107,12.10,7-0,7.107,12=107,12.(10,7-0,7)=107,12.10=1071,2$.
Dùng quy tắc dấu ngoặc:
$11,1+(1-2,1)=11,1+1-2,1=11,1-2,1+1=10$.
$91,5-(13+11)=91,5-13-11=91,5-11-13=67,5$.
$54,15-(-213,1-6)=54,15+213,1+6=54,15+6+213,1=273,25$.
Làm tròn số thập phân
Hàng quy tròn: hàng được làm tròn.
Chữ số bên phải nhỏ hơn 5: giữ nguyên
Làm tròn đến hàng chục:
$131,54\approx 130$ (số 3 là hàng chục, số bên phải là 1 nhỏ hơn 5)
$254\approx 250$
Làm tròn đến hàng phần chục:
$131,54\approx 131,5$ (số 5 là hàng phần chục, số bên phải là 4 nhỏ hơn 5)
$154,203\approx 154,2$
Chữ số bên phải từ 5 trở lên: tăng lên 1 đơn vị
Làm tròn đến hàng đơn vị:
$131,54\approx 132$ (số 1 là hàng đơn vị, số bên phải là 5)
$254,799\approx 255$
Làm tròn đến hàng phần trăm:
$131,74891\approx 131,75$ (số 4 là hàng phần trăm, số bên phải là 8 lớn hơn 5)
$154,2073\approx 154,21$
Ước lượng kết quả
$11,5.99,9\approx 12.100=1200$
$15,001.9,85\approx 15.10=150$
Tỉ số của 2 đại lượng
Thương trong phép chia $a:b$ được gọi là tỉ số của $a$ và $b$.
Tỉ số của $a$ và $b$ kí hiệu là $a:b$ hoặc $\frac{a}{b}$.
Tỉ số phần trăm của 2 đại lượng
Kí hiệu % thay cho $\frac{1}{100}$.
Tỉ số phần trăm của 1 và 2 là: $1:2=\frac{1}{2}=\frac{1.100}{2}$% $=50$%
Tỉ số phần trăm của 5 và 7 là: $5:7=\frac{5}{7}=\frac{5.100}{7}$% $\approx 71,4$%
Tìm giá trị phần trăm của 1 số
Giá trị $50$% của 20 là: $50$%.$20=\frac{50}{100}.20=10$.
Giá trị $30$% của 66 là: $30$%.$66=\frac{30}{100}.66=19,8$.
Giá trị $a$% của $b$ là: $a$%.$b=\frac{a}{100}.b$.
Tìm 1 số khi biết giá trị phằn trăm của nó
Nếu $50$% của $x$ là 30 thì $50$%.$x=30$. Nên $x=30:50$%$=30.\frac{100}{50}=60$.
Nếu $40$% của $y$ là 80 thì $40$%.$y=80$. Nên $y=80:40$%$=\frac{100}{40}=200$.
Nếu $50$% của $x$ là 30 thì $50$%.$x=30$. Nên $x=30:50$%$=30.\frac{100}{50}=60$.
Nếu $a$% của $x$ là $b$ thì $a$%.$x=b$. Nên $x=b:a$%$=b.\frac{100}{a}$.
Sử dụng tỉ số phần trăm trong thực tế
Bài toán 1: mua bán hằng ngày
Món A trong siêu thị giá gốc là 1 300 000 và được giảm giá 7%.
Số tiền phải trả chiếm: 100% – 7% = 93% giá gốc.
Số tiền cần thiết để mua món A là: 93%.1 300 000 = $\frac{93.1 300 000}{100}$ = 1 209 000.
Món B sau khi giảm 20% sẽ có giá 400 000.
Giá này chiếm: 100% – 20% = 80% giá gốc.
Vậy giá gốc của món B là: 400 000: 80% = $\frac{400 000.100}{80}$.
Bài toán 2: lãi suất tín dụng
Khách hàng A gởi tiết kiệm 80 triệu không kì hạn với lãi suất 0,3%/năm.
Số tiền lãi nhận được sau 1 năm là: $80 000 000.0,3$%$=240 000$.
Khi gởi không kì hạn, ngân hàng sẽ tính số ngày trong 1 năm là 360 ngày.
Số tiền lãi người A nhận được sau 60 ngày là: $240 000.\frac{60}{360}=40 000$.
Khách hàng B gởi tiết kiệm 80 triệu có kì hạn 6 tháng với lãi suất 7%/năm.
Số tiền lãi người B nhận được sau 6 tháng là: $80 000 000.7$%.$\frac{6}{12}=2 800 000$.
Bài toán 3: thành phần các chất trong hóa học
Hòa tan hết 20g muối vào 180g nước.
Tổng khối lượng dung dịch là: 20 + 180 = 200g.
Tỉ số phần trăm muối trong dung dịch là: $\frac{20.100}{200}$%$=10$%.
Tỉ số phần trăm
Chương 7.
Hình có trục đối xứng. Trục đối xứng
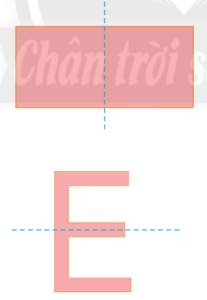
Đường nét đứt là trục đối xứng của các hình trên.
Khi gấp theo đường nét đứt, hai phần của mỗi hình sẽ chống khít lên nhau.
Bên dưới cũng là các hình có trục đối xứng.
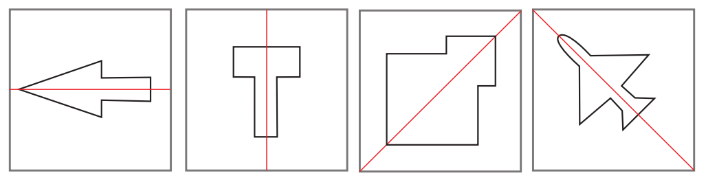
Nhận biết những hình phẳng có trục đối xứng

2 hình bên trái có trục đối xứng, còn hình bên phải thì không.
Hình có tâm đối xứng. Tâm đối xứng
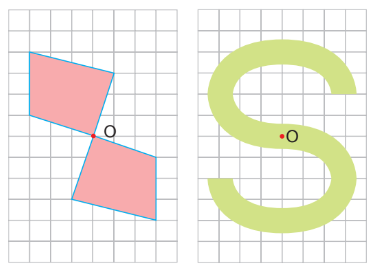
Điểm màu đỏ là tâm đối xứng của mỗi hình trên.
Hai hình dưới không có tâm đối xứng.
Nhận biết những hình phẳng có tâm đối xứng

Hình a,b có tâm đối xứng, còn hình c thì không.
Vẻ đẹp của thế giới tự nhiên biểu hiện qua tính đối xứng

Tính đối xứng trong khoa học kĩ thuật và đời sống



Chương 8.
Điểm
Khi nói tới 2 điểm, mà không nói gì thêm, ta coi đó là 2 điểm phân biệt, không trùng nhau.
Từ các điểm, ta xây dựng được các hình. Mỗi hình là 1 tập hợp các điểm. Một điểm cũng được coi là 1 hình.
Đường thẳng
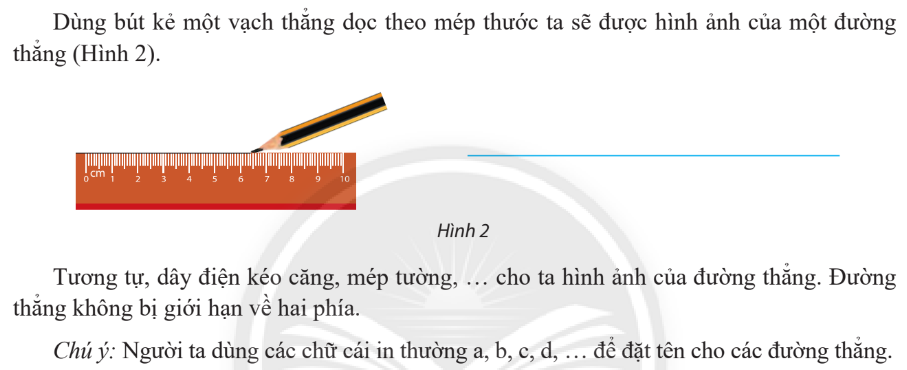
Vẽ đường thẳng

Có 1 và chỉ 1 đường thẳng đi qua 2 điểm phân biệt cho trước.
Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng

Điểm $A$ thuộc đường thẳng $d$, kí hiệu $A\in d$.
Điểm $B$ không thuộc đường thẳng $d$, kí hiệu $B\not\in d$.

Trên đường thẳng $t$ có 2 điểm $C,D$ nên ta có thể gọi đường thẳng là $CD$ hoặc $DC$.
