Test21 | Tích phân trong hình học
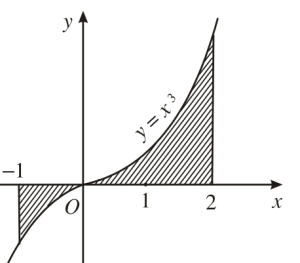
Diện tích phần gạch chéo $S=$
- A. $\int_{-1}^{2}x^3dx$
- B. $\int_{-1}^{2}|x^3|dx$

Diện tích phần gạch chéo $S=$
- A. $\int_{-1}^{0}x^3dx+\int_{0}^{2}x^3dx$
- B. $-\int_{-1}^{0}x^3+\int_{0}^{2}x^3dx$

Diện tích phần gạch chéo $S=$
- A. $\frac{17}{4}$
- B. $\frac{7}{4}$
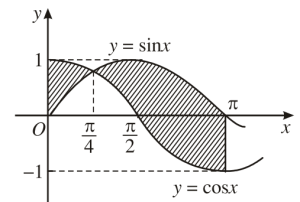
Diện tích phần gạch chéo $S=$
- A. $\int_0^{\pi}\left ( \sin x-\cos x \right )dx$
- B. $\int_0^{\pi}\left ( \cos x-\sin x \right )dx$
- C. $\int_0^{\pi}\left | \sin x-\cos x \right |dx$
- D. $\int_0^{\pi}\left | \cos x-\sin x \right |dx$
C, D

Diện tích phần gạch chéo $S=$
- A. $\int_0^{\frac{\pi}{4}}\left ( \cos x-\sin x \right )dx+\int_{\frac{\pi}{4}}^{\pi}\left ( \sin x-\cos x \right )dx$
- B. $\int_0^{\frac{\pi}{4}}\left ( \sin x-\cos x \right )dx+\int_{\frac{\pi}{4}}^{\pi}\left ( \cos x-\sin x \right )dx$

Diện tích phần gạch chéo $S=$
- A. $2\sqrt{2}$
- B. $1-\sqrt{2}$
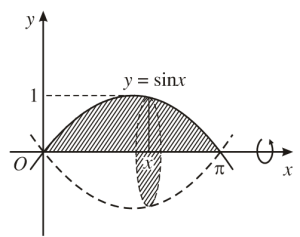
Nếu xoay đường cong quanh trục $x$ thì tạo ra 1 khối có thể tích $V=$
- A. $\pi \int_0^\pi \sin ^2 x dx$
- B. $\pi \int_0^\pi |\sin x| dx$
- C. $ \int_0^\pi \sin ^2 x dx$

Cho công thức $\sin^2x=\frac{1}{2}\left ( 1-\cos 2x \right )$. Nếu xoay đường cong quanh trục $x$ thì tạo ra 1 khối có thể tích $V=$
- A. $\pi\int_0^\pi(1-\cos 2 x) dx$
- B. $\frac{\pi}{2} \int_0^\pi(1-\cos 2 x) dx$

Nếu xoay đường cong quanh trục $x$ thì tạo ra 1 khối có thể tích $V=$
- A. $\frac{\pi^2}{2}$
- B. $\pi^2$
- C. $2\pi$
- D. $\frac{\pi}{4}$

