Test7 | Lấy mẫu và phân phối mẫu
Chỉ ra tình huống nào sau đây liên quan đến việc lấy mẫu từ một quần thể hữu hạn và tình huống nào liên quan đến việc lấy mẫu từ một quần thể vô hạn.
a. Lấy mẫu tài xế được cấp phép ở bang New York.
b. Lấy mẫu hộp ngũ cốc do công ty Breakfast Choice sản xuất.
c. Lấy mẫu ô tô đi qua Cầu Cổng Vàng vào một ngày trong tuần điển hình.
d. Lấy mẫu sinh viên trong khóa học thống kê tại Đại học Indiana.
e. Lấy mẫu đơn đặt hàng được xử lý bởi công ty đặt hàng qua thư.
a. Lấy mẫu tài xế được cấp phép ở bang New York -> hữu hạn
b. Lấy mẫu hộp ngũ cốc do công ty Breakfast Choice sản xuất -> vô hạn
c. Lấy mẫu ô tô đi qua Cầu Cổng Vàng vào một ngày trong tuần điển hình -> hữu hạn
d. Lấy mẫu sinh viên trong khóa học thống kê tại Đại học Indiana -> hữu hạn
e. Lấy mẫu đơn đặt hàng được xử lý bởi công ty đặt hàng qua thư -> vô hạn
Nhiều loại thuốc dùng để điều trị ung thư rất đắt tiền. BusinessWeek báo cáo về chi phí cho mỗi lần điều trị Herceptin, một loại thuốc dùng để điều trị ung thư vú (BusinessWeek, ngày 30 tháng 1 năm 2006).
Chi phí điều trị điển hình (bằng đô la) cho Herceptin được cung cấp bởi một mẫu ngẫu nhiên đơn giản gồm 10 bệnh nhân.
| 4376 | 5578 | 2717 | 4920 | 4495 |
| 4798 | 6446 | 4119 | 4237 | 3814 |
a. Xây dựng ước tính điểm về chi phí trung bình cho mỗi lần điều trị bằng Herceptin.
b. Xây dựng ước tính điểm về độ lệch chuẩn của chi phí cho mỗi lần điều trị bằng Herceptin.
a. Ước tính điểm về chi phí trung bình cho mỗi lần điều trị bằng Herceptin là: 4550
b. Ước tính điểm về độ lệch chuẩn của chi phí cho mỗi lần điều trị bằng Herceptin là: 1003,8
Một mẫu gồm 50 công ty Fortune 500 (Fortune, ngày 14 tháng 4 năm 2003) cho thấy 5 công ty có trụ sở tại New York, 6 công ty ở California, 2 công ty ở Minnesota và 1 công ty ở Wisconsin.
a. Xây dựng ước tính về tỷ lệ của các công ty Fortune 500 có trụ sở tại New York.
b. Xây dựng ước tính về số lượng các công ty Fortune 500 có trụ sở tại Minnesota.
c. Xây dựng ước tính về tỷ lệ các công ty trong Fortune 500 không có trụ sở tại bốn tiểu bang này.
a. Ước tính về tỷ lệ của các công ty Fortune 500 có trụ sở tại New York là: 5/50=0,1
b. Ước tính về số lượng các công ty Fortune 500 có trụ sở tại Minnesota là: 2
c. Ước tính về tỷ lệ các công ty trong Fortune 500 không có trụ sở tại bốn tiểu bang này là: (50-14)/50=36/50=0,72
Barron’s báo cáo rằng số tuần trung bình mà một cá nhân thất nghiệp là 17,5 tuần (Barron’s, 18 tháng 2 năm 2008). Giả sử rằng đối với dân số gồm tất cả những người thất nghiệp, thời gian thất nghiệp trung bình của dân số là 17,5 tuần và độ lệch chuẩn của dân số là 4 tuần. Giả sử bạn muốn chọn một mẫu ngẫu nhiên gồm 50 cá nhân thất nghiệp cho nghiên cứu tiếp theo.
a. Hiển thị phân phối mẫu của trung bình mẫu của 50 cá nhân thất nghiệp.
b. Xác suất để một mẫu ngẫu nhiên đơn giản gồm 50 cá nhân thất nghiệp sẽ cung cấp giá trị trung bình mẫu trong vòng 1 tuần so với giá trị trung bình của tổng thể là bao nhiêu?
a.
$E(\overline{x})=17,5$.
$\sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}=\frac{4}{\sqrt{50}}=0,57$
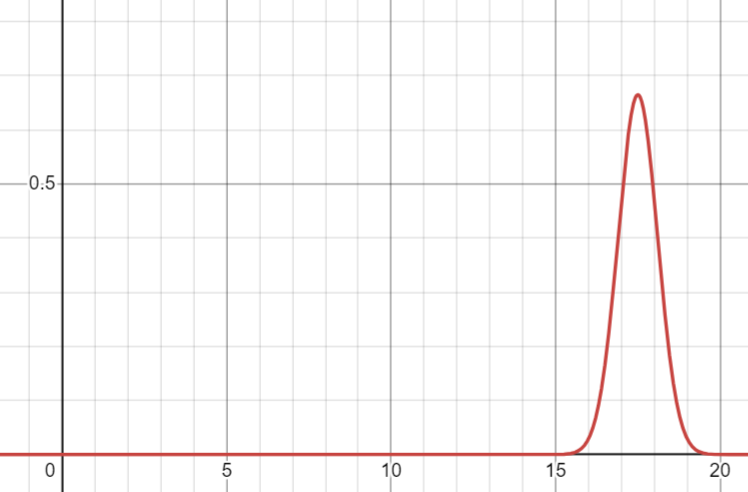
b.
b. Xác suất để một mẫu ngẫu nhiên đơn giản gồm 50 cá nhân thất nghiệp sẽ cung cấp giá trị trung bình mẫu trong vòng 1 tuần so với giá trị trung bình của tổng thể là: $P(16,5<\overline{x}<18,5)$
$z=\overline{x}-17,5/0,57$
$16,5<\overline{x}<18,5$ => $-1,75<z<1,75$
$P(z>1,75)=1-P(z<1,75)=1-0,9599=0,0401$
$P(16,5<\overline{x}<18,5)=P(-1,75<z<1,75)=1-2.P(z>1,75)=1-2.0,0401=0,9198$
College Board đã báo cáo điểm trung bình sau đây cho ba phần của Bài kiểm tra năng lực học thuật (SAT) (The World Almanac, 2009):
Đọc 502
Toán 515
Viết 494
Giả sử rằng độ lệch chuẩn tổng thể trên mỗi phần của bài kiểm tra là σ=100.
a. Xác suất một mẫu ngẫu nhiên gồm 90 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu trong khoảng 10 điểm so với trung bình tổng thể là 502 trong phần Đọc của bài kiểm tra là bao nhiêu?
b. Xác suất mà một mẫu ngẫu nhiên gồm 90 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu trong khoảng 10 điểm so với điểm trung bình tổng thể là 515 trong phần Toán của bài kiểm tra là bao nhiêu? So sánh xác suất này với giá trị tính được ở phần (a).
c. Xác suất một mẫu ngẫu nhiên gồm 100 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu nằm trong phạm vi 10 của tổng số trung bình 494 trong phần viết của bài kiểm tra là bao nhiêu? Nhận xét về sự khác biệt giữa xác suất này và các giá trị tính toán ở phần (a) và (b).
a.
Trung bình: 502
Sai số chuẩn: 10,54
Xác suất một mẫu ngẫu nhiên gồm 90 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu trong khoảng 10 điểm so với trung bình tổng thể là 502 trong phần Đọc của bài kiểm tra là: P(492<x<512)=P(-0,95<z<0,95)=2P(z<0,95)-1=2.0,8289-1=0,6578
b. Xác suất mà một mẫu ngẫu nhiên gồm 90 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu trong khoảng 10 điểm so với điểm trung bình tổng thể là 515 trong phần Toán của bài kiểm tra là: P(505<x<525)=0,6578
c. Xác suất một mẫu ngẫu nhiên gồm 100 người làm bài kiểm tra sẽ cung cấp điểm kiểm tra trung bình mẫu nằm trong phạm vi 10 của tổng số trung bình 494 trong phần viết của bài kiểm tra là: P(484<x<504)=0,6578
Để ước tính độ tuổi trung bình của dân số 4000 nhân viên, một mẫu ngẫu nhiên đơn giản gồm 40 nhân viên được chọn.
a. Bạn có sử dụng hệ số hiệu chỉnh tổng thể hữu hạn để tính sai số chuẩn của giá trị trung bình không? Giải thích.
b. Nếu độ lệch chuẩn của tổng thể là σ=8,2 năm, hãy tính sai số chuẩn khi có và không có hệ số hiệu chỉnh tổng thể hữu hạn. Lý do cơ bản để bỏ qua hệ số hiệu chỉnh tổng thể hữu hạn bất cứ khi nào n/N<0,05 là gì?
c. Xác suất để tuổi trung bình của mẫu của nhân viên sẽ cách tuổi trung bình của dân số trong vòng 2 năm là bao nhiêu?
a. Không cần sử dụng hệ số hiệu chỉnh tổng thể hữu hạn để tính sai số chuẩn của giá trị trung bình vì n/N<0,05
b. Độ lệch chuẩn của tổng thể là σ=8,2 năm.
Sai số chuẩn khi có hệ số hiệu chỉnh tổng thể hữu hạn là: 1,297
Sai số chuẩn khi không có hệ số hiệu chỉnh tổng thể hữu hạn là: 1,29
Lý do cơ bản để bỏ qua hệ số hiệu chỉnh tổng thể hữu hạn bất cứ khi nào n/N<0,05 là chúng có sai lệch không đáng kể.
c. Xác suất để tuổi trung bình của mẫu của nhân viên sẽ cách tuổi trung bình của dân số trong vòng 2 năm là: P(-1,54<z<1,54)=2.P(z>1,54)-1=2.0,9382-1=0,8764
Chủ tịch của Doerman Distributions, Inc., tin rằng 30% đơn đặt hàng của công ty đến từ những khách hàng lần đầu. Một mẫu ngẫu nhiên gồm 100 đơn hàng sẽ được sử dụng để ước tính tỷ lệ khách hàng lần đầu.
a. Giả sử rằng chủ tịch đúng và p=.30. Phân phối mẫu của nghiên cứu này là gì?
b. Xác suất để tỷ lệ mẫu nằm trong khoảng từ 0,20 đến 0,40 là bao nhiêu?
a.
np và n(1-p) lớn hơn 5 nên: Phân phối mẫu của nghiên cứu này là phân phối chuẩn.
b.
$\mu=0,3$
$\sigma_{\overline{p}}=\sqrt{\frac{0,3(1-0,3)}{100}}=0,0458$.
Xác suất để tỷ lệ mẫu nằm trong khoảng từ 0,20 đến 0,40 là: P(0,2<x<0,4)
z=x-0,3/0,0458
0,2<x<0,4 => -2,18<z<2,18
P(0,2<x<0,4)=P(-2,18<z<2,18)=2P(z>2,18)-1=2.0,9854-1=0,9708

