**Section II. INVESTORS AND MARKETS
****PART ONE. INVESTMENT DECISION RULES
Chapter 15. THE FINANCIAL MARKETS
Now let’s talk finance
This section will analyse the behaviour of the investor who buys financial instruments that the financial manager is trying to sell. Investors are free to buy a security or not and, if they decide to buy it, they are then free to hold it or resell it in the secondary market.
The financial investor seeks two types of returns: the risk-free interest rate (which we call the time value of money) and a reward for risk-taking. This section looks at these two types of returns in detail but, first, here are some general observations about financial markets.
Section 15.1 THE ROLE OF CAPITAL MARKETS
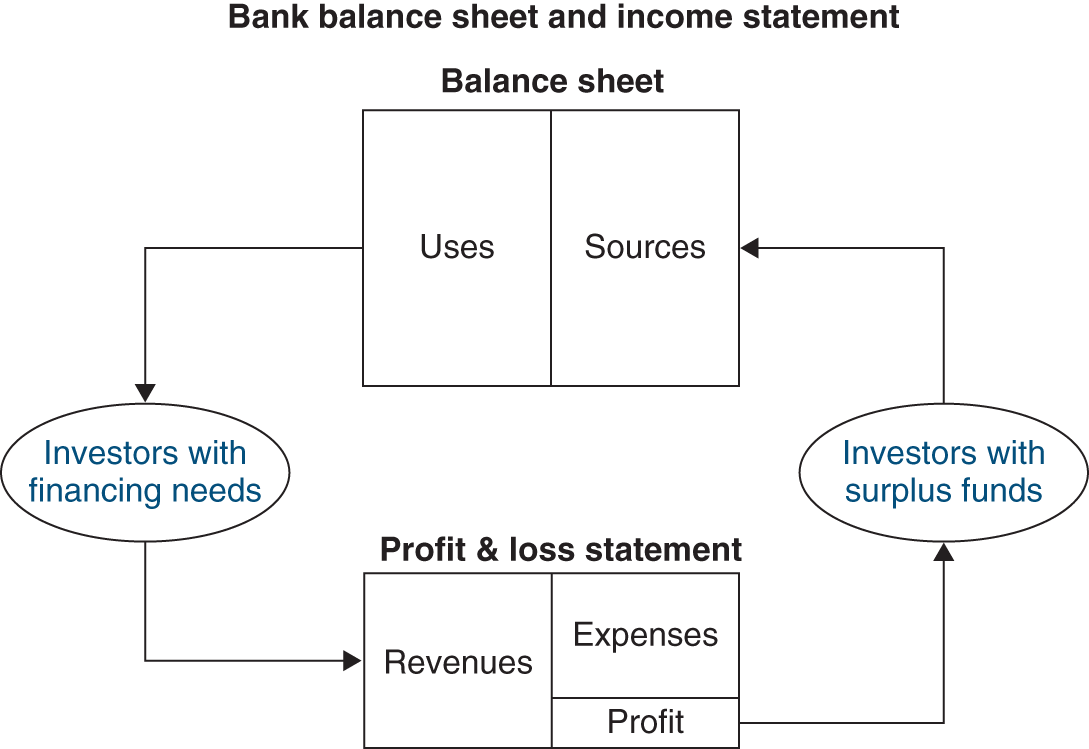
The primary role of a financial system is to bring together economic agents with surplus financial resources, such as households, and those with net financial needs, such as companies and governments. This relationship is illustrated below:

To use the terminology of John Gurley and Edward Shaw (1960), the parties can be brought together directly or indirectly.
In the first case, known as direct finance, the parties with excess financial resources directly finance those with financial needs. The financial system serves as a broker, matching the supply of funds with the corresponding demand. This is what happens when an individual shareholder subscribes to a listed company’s share issue or when a bank places a corporate bond issue with individual investors.
In the second case, or indirect finance, financial intermediaries, such as banks, buy “securities” – i.e. loans – “issued” by companies. The banks in turn collect funds, in the form of demand or savings deposits, or issue their own securities that they place with investors. In this model, the financial system serves as a gatekeeper between suppliers and users of capital and performs the function of intermediation.
When you deposit money in a bank, the bank uses your money to make loans to companies. Similarly, when you buy bonds issued by a financial institution, you enable the institution to finance the needs of other industrial and commercial enterprises through loans. Lastly, when you buy an insurance policy, you and other investors pay premiums that the insurance company uses to invest in the bond market, the property market, etc.
This activity is called intermediation, and is very different from the role of a mere broker in the direct finance model.
With direct finance, the amounts that pass through the broker’s hands do not appear on its balance sheet, because all the broker does is to put the investor and issuer in direct contact with each other. Only brokerage fees and commissions appear on a brokerage firm’s profit and loss, or income, statement.
In intermediation, the situation is very different. The intermediary shows all resources on the liabilities side of its balance sheet, regardless of their nature: from deposits to bonds to shareholders’ equity. Capital serves as the creditors’ ultimate guarantee. On the assets side, the intermediary shows all uses of funds, regardless of their nature: loans, investments, etc. The intermediary earns a return on the funds it employs and pays interest on the resources. These cash flows appear in its income statement in the form of revenues and expenses. The difference, or spread, between the two constitutes the intermediary’s earnings.
The intermediary’s balance sheet and income statement thus function as holding tanks for both parties – those who have surplus capital and those who need it:
Today’s economy is experiencing increasing disintermediation, characterised by the following phenomena:
- more companies are obtaining financing directly from capital markets; and
- more companies and individuals are investing directly in capital markets.
When capital markets are underdeveloped, an economy functions primarily on debt financing. Conversely, when capital markets are sufficiently well developed, companies are no longer restricted to debt, and they can then choose to increase their equity financing. Taking a page from the economist John Hicks, it is possible to speak of bank-based economies and market-based economies.
In a bank-based economy, the capital market is underdeveloped and only a small portion of corporate financing needs are met through the issuance of securities. Therefore, bank financing predominates. Companies borrow heavily from banks, whose refinancing needs are mainly covered by the central bank.
The lender’s risk is that the corporate borrower will not generate enough cash flow to service the debt and repay the principal, or amount of the loan.
In a market-based economy, companies cover most of their financing needs by issuing financial securities (shares, bonds, commercial paper, etc.) directly to investors. A capital market economy is characterised by direct solicitation of investors’ funds. Economic agents with surplus resources invest a large portion of their funds directly in the capital markets by buying companies’ shares, bonds, commercial paper or other short-term negotiable debt. They do this either directly or through mutual funds. Intermediation gives way to the brokerage function, and the business model of financial institutions evolves towards the placement of companies’ securities directly with investors.
In this economic model, bank loans are extended primarily to households in the form of consumer credit, mortgage loans, etc., as well as to small enterprises that do not have access to the capital markets.
The following graphs provide the best illustration of the rising importance of capital markets.
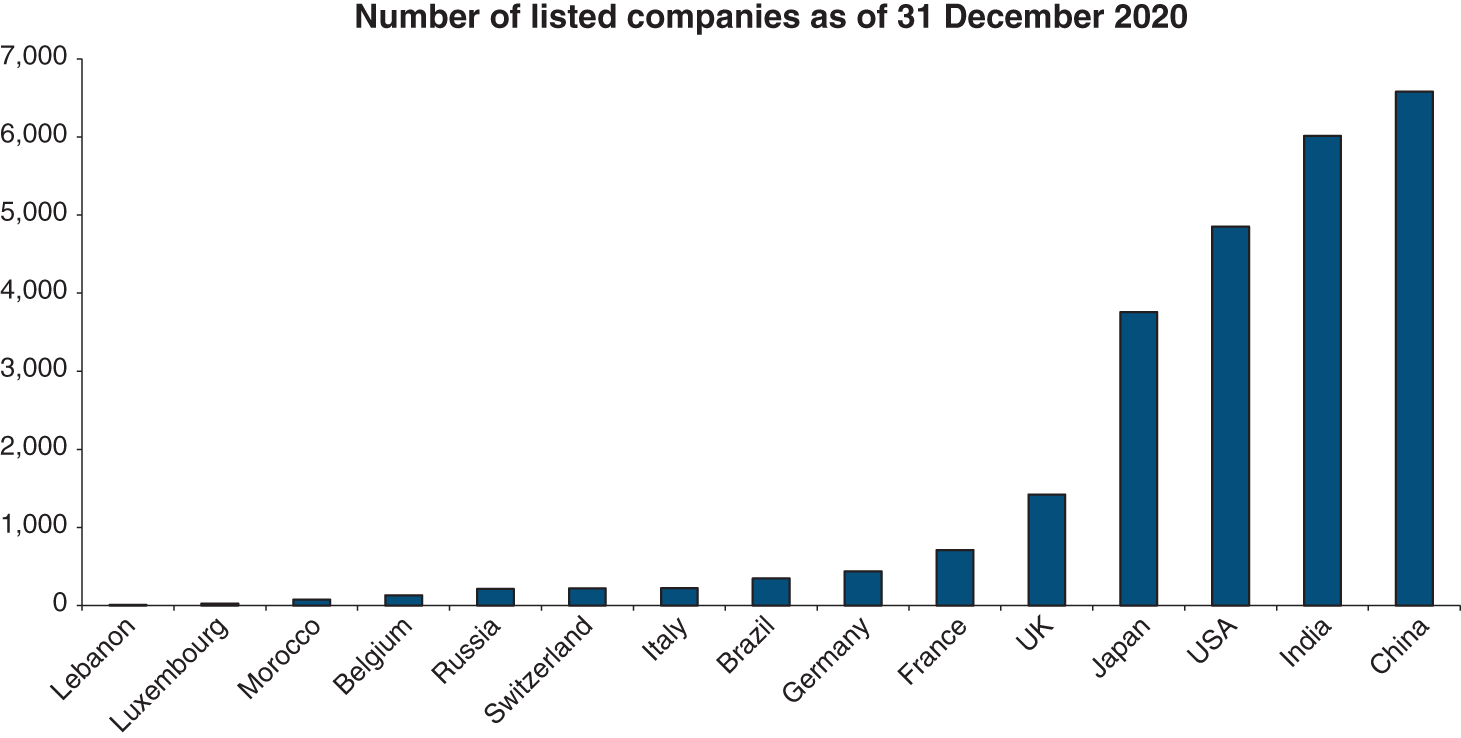
…be it in terms of the number of listed companies…
Note: Domestic companies only.
Source: Data from World Federation of Exchanges, NYSE-Euronext, London Stock Exchange, Bourse de Casablanca, Bolsa Madrid, Beirut Stock Exchange, Borsa Italiana
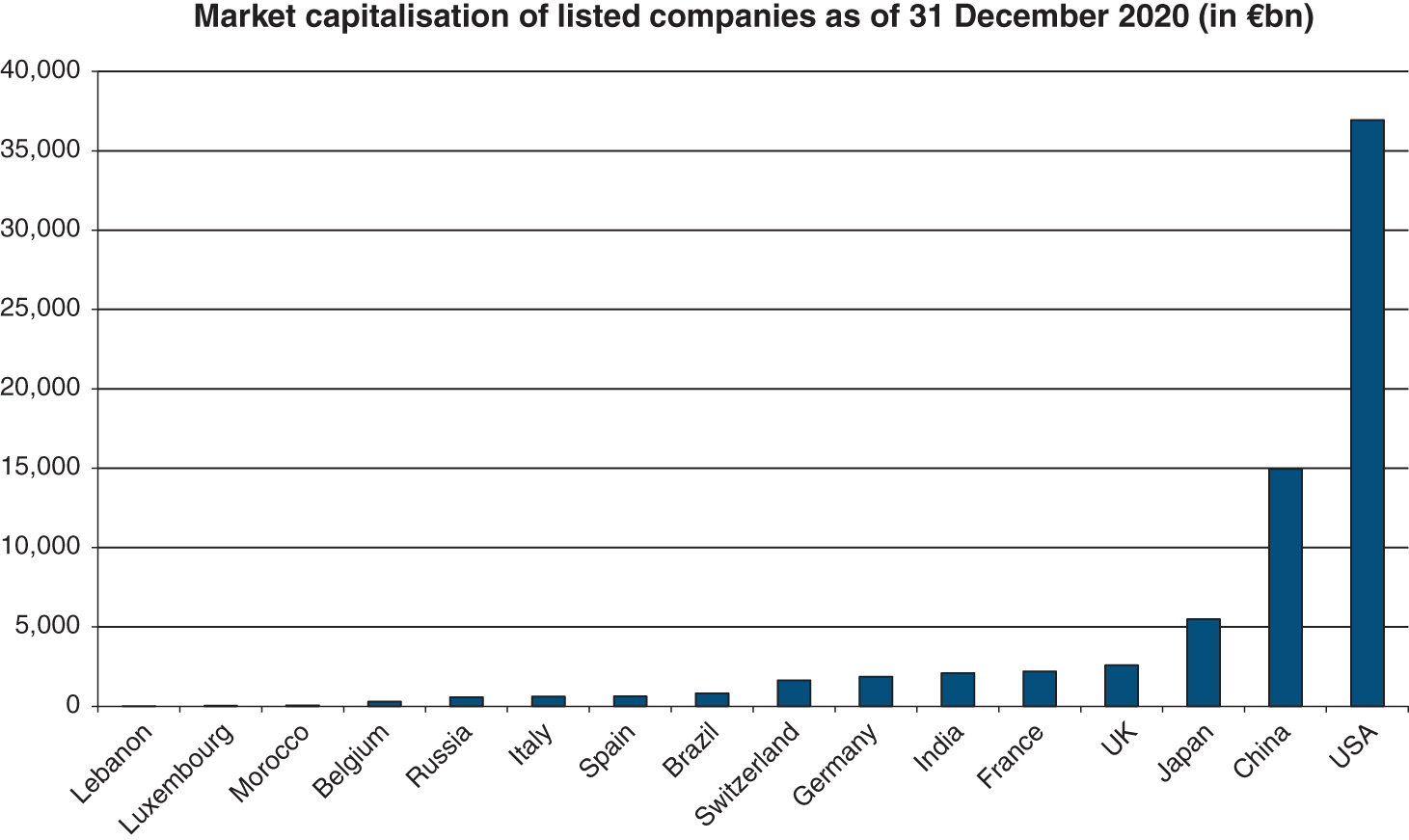
Source: Data from World Federation of Exchanges, NYSE-Euronext, Beirut Stock exchange, Borsa Italiana, London Stock Exchange
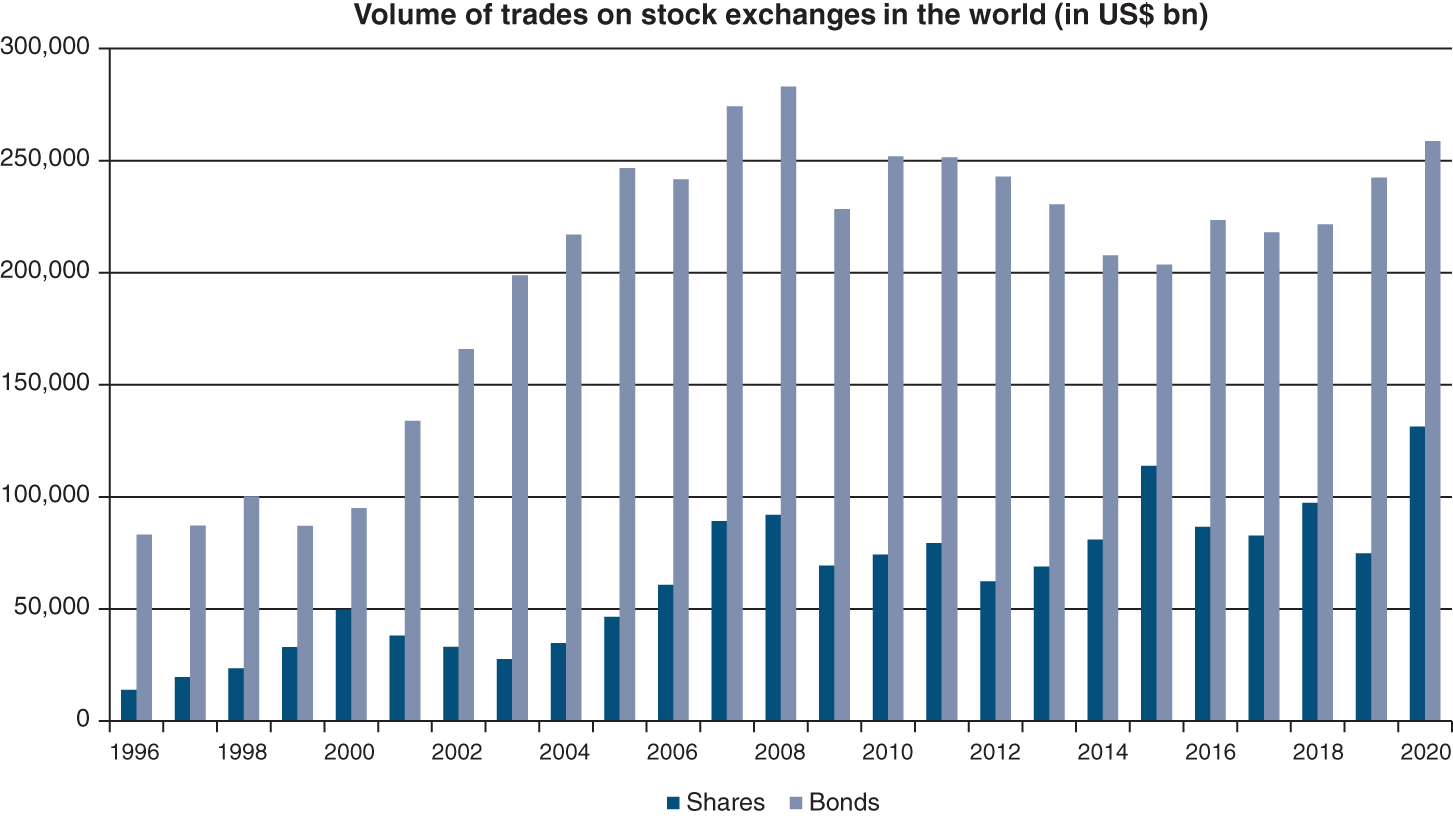
Source: Data from World Federation of Exchanges, SIFMA
Section 15.2 PRIMARY, SECONDARY AND DERIVATIVE MARKETS
1/ FROM THE PRIMARY MARKET TO THE SECONDARY MARKET
The new issues market (i.e. creation of securities) is called the primary market. Subsequent transactions involving these securities take place on the secondary market. Both markets, like any market, are defined by two basic elements: the product (the security) and the price (its value).
Thus, shares issued or created when a company is founded can later be floated on a stock exchange, just as long-term bonds may be used by speculators for short-term strategies. The life of a financial security is intimately connected with the fact that it can be bought or sold at any moment.
From the point of view of the company, the distinction between the primary and secondary markets is fundamental. The primary market is the market for “new” financial products, from equity issues to bond issues and everything in between. It is the market for newly minted financial securities where the company can raise fresh money.
Conversely, the secondary market is the market for “used” financial products. Securities bought and sold on this market have already been created and are now simply changing hands, without any new securities being created and consequently without any new money for the company.
The primary market enables companies, financial institutions, governments and local authorities to obtain financial resources by issuing securities. These securities are then listed and traded on secondary markets. The job of the secondary market is to ensure that securities are properly priced and traded. This is the essence of liquidity: facilitating the purchase or sale of a security.
The distinction between primary and secondary markets is conceptual only. The two markets are not separated from each other. A given financial investor can buy either existing shares or new shares issued during a capital increase, for example.
If there is often more emphasis placed on the primary market, it is because the function of the financial markets is, first and foremost, to ensure equilibrium between financing needs and the sources of finance. Secondary markets, where securities can change hands, constitute a kind of financial “innovation”.
2/ THE FUNCTION OF THE SECONDARY MARKET
Financial investors do not intend to remain invested in a particular asset indefinitely. Even before they buy a security, they begin thinking about how they will exit. As a result, they are constantly evaluating whether they should buy or sell such and such an asset.
Monetising is relatively easy when the security is a short-term one. All the investor has to do is wait until maturity. The need for an exit strategy grows with the maturity of the investment and is greatest for equity investments, whose maturity is unlimited. The only way a shareholder can exit their investment is to sell their shares to someone else.
As an example, the successful business person who floats their company on the stock exchange, thereby selling part of their shares to new shareholders, diversifies their own portfolio, which before flotation was essentially concentrated in one investment.
Liquidity refers to the ability to convert an instrument into cash quickly and without loss of value. It affords the opportunity to trade a financial instrument at a “listed” price and in large quantities without disrupting the market. An investment is liquid when an investor can buy or sell it in large quantities without causing a change in its market price.
The secondary market is therefore a zero-sum game between investors, because what one investor buys, another investor sells. In principle, the secondary market operates completely independently from the issuer of the securities.
A company that issues a bond today knows that a certain amount of funds will remain available in each future year. This knowledge is based on the bond’s amortisation schedule. During that time, however, the investors holding the bonds will have changed.
Secondary market transactions do not show up in macroeconomic statistics on capital formation, earning them the scorn of some observers who claim that the secondary market does nothing to further economic development, but only bails out the initial investors.
We believe this thinking is misguided and reflects great ignorance about the function of secondary markets in the economy. Remember that a financial investor is constantly comparing the primary and secondary markets. They care little whether a “new” or a “used” security is being bought, so long as they have the same characteristics.
In fact, the quality of a primary market for a security depends greatly on the quality of its secondary market. Think about it: who would want to buy a financial security on the primary market, knowing that it will be difficult to sell it on the secondary market?
The secondary market determines the price at which the company can issue its securities on the primary market, because investors are constantly deciding between existing investments and proposed new investments.
We have seen that it would be a mistake to think that a financial manager takes no interest in the secondary market for the securities issued by the company. On the contrary, it is on the secondary market that the company’s financial “raw material” is priced every day. When the raw material is equities, there is another reason the company cannot afford to turn its back on the secondary market: this is where investors trade the voting rights in the company’s affairs and, by extension, control of the company.
3/ DERIVATIVE MARKETS: FUTURES AND OPTIONS
Derivative markets are where securities that derive their value from another asset (share, bond, commodity or even climate index) are traded. There are two main types of derivative products: options (which we will develop in Chapter 23 as they have become a key matter in financial theory and practice) and futures (Chapter 51).
Derivative instruments are tailored especially to the management of financial risk. By using derivatives, the financial manager chooses a price – expressed as an interest rate, an exchange rate or the price of a raw material – that is independent of the company’s financing or investment term. Derivatives are also highly liquid. The financial manager can change their mind at any time at a minimal cost.
Options and futures allow one to take important risks with a reduced initial outlay due to their leverage effect (this is called speculation), or on the contrary to transfer risks to a third party (hedging), and this is what companies normally use them for.
Section 15.3 THE FUNCTIONS OF A FINANCIAL SYSTEM
The job of a financial system is to efficiently create financial liquidity for those investment projects that promise the highest profitability and that maximise collective utility.
However, unlike other types of markets, a financial system does more than just achieve equilibrium between supply and demand. A financial system allows investors to convert current revenues into future consumption. It also provides current resources for borrowers, at the cost of reduced future spending.
Robert Merton and Zvi Bodie have isolated six essential functions of a financial system:
- A financial system provides means of payment to facilitate transactions. Cheques, debit and credit cards, electronic transfers, bitcoins, etc. are all means of payment that individuals can use to facilitate the acquisition of goods and services. Imagine if everything could only be paid for with bills and coins!
- A financial system provides a means of pooling funds for financing large, indivisible projects. A financial system is also a mechanism for subdividing the capital of a company so that investors can diversify their investments. If factory owners had to rely on just their own savings, they would very soon run out of investible funds. Indeed, without a financial system’s support, Nestlé and British Telecom would not exist. The system enables the entrepreneur to gain access to the savings of millions of individuals, thereby diversifying and expanding their sources of financing. In return, the entrepreneur is expected to achieve a certain level of performance. Returning to our example of a factory, if you were to invest in your neighbour’s steel plant, you might have trouble getting your money back if you should suddenly need it. A financial system enables investors to hold their assets in a much more liquid form: shares, bank accounts, etc.
- A financial system distributes financial resources across time and space, as well as between different sectors of the economy. The financial system allows capital to be allocated in a myriad of ways. For example, young people can borrow to buy a house or people approaching retirement can save to offset future decreases in income. Even a developing nation can obtain resources to finance further development. And when an industrialised country generates more savings than it can absorb, it invests those surpluses through financial systems. In this way, “old economies” use their excess resources to finance “new economies”.
- A financial system provides tools for managing risk. It is particularly risky (and inefficient as we will see later) for an individual to invest all of their funds in a single company because, if the company goes bankrupt, they lose everything. By creating collective savings vehicles, such as mutual funds, brokers and other intermediaries enable individuals to reduce their risk by diversifying their exposure. Similarly, an insurance company pools the risk of millions of people and insures them against risks they would otherwise be unable to assume individually.
- A financial system provides price information at very low cost. This facilitates decentralised decision-making. Asset prices and interest rates constitute information used by individuals in their decisions about how to consume, save or divide their funds among different assets. But research and analysis of the available information on the financial condition of the borrower is time-consuming, costly and typically beyond the scope of the layperson. Yet when a financial institution does this work on behalf of thousands of investors, the cost is greatly reduced.
- A financial system provides the means for reducing conflict between the parties to a contract. Contracting parties often have difficulty monitoring each other’s behaviour. Sometimes conflicts arise because each party has different amounts of information and divergent contractual ties. For example, an investor gives money to a fund manager in the hope that they will manage the funds in the investor’s best interests (and not their own!). If the fund manager does not uphold their end of the bargain, the market will lose confidence in them. Typically, the consequence of such behaviour is that they will be replaced by a more conscientious manager.
Section 15.4 THE RELATIONSHIP BETWEEN BANKS AND COMPANIES
Not so long ago, banks could be classified as:
- Commercial banks that schematically collected funds from individuals and lent to corporates.
- Investment banks that provided advisory services (mergers and acquisitions, wealth management) and played the role of a broker (placement of shares, of bonds) but without “using their balance sheet”.
Since the beginning of this century, large financial conglomerates have emerged both in the US and Europe. This resulted from mega-mergers between commercial banks and investment banks: BNP/Paribas, Citicorp/Travelers Group, Chase Manhattan/JP Morgan, Bank of America/Merrill Lynch, or the transition by investment banks towards commercial banking (Goldman Sachs, Mediobanca) or the reverse (Credit Suisse, Credit Agricole).
This trend, eased by changes in regulation (in particular in the US with the reform of the Glass–Steagall Act in 1999), shows a willingness of large banking groups to adopt the business model of a universal bank (also called “one-stop shopping”) in a context of increasing internationalisation and complexity. This is particularly true for certain business lines like corporate finance or fund management, in which size constitutes a real competitive advantage.
Following the 2008 financial crisis, there emerged a certain political willingness to split up large banking groups again, specifically in order to separate deposits from market-related activities. This idea (not only guided by the protection of households’ deposits) has only partially materialised in laws (in the US, France, the UK) aimed mainly at confining speculative operations and avoiding market activities that put clients’ deposits at risk (Volker regulation in particular).
Large banking groups now generally include the following business lines:
- Retail banking: for individuals and small and medium-sized corporates. Retail banks serve as intermediaries between those who have surplus funds and those who require financing. The banks collect resources from the former and lend money to the latter. They have millions of clients and therefore adopt an industrial organisation. The larger the bank’s portfolio, the lower the risk – thanks once again to the law of large numbers. Retail banking is an extremely competitive activity. After taking into account the cost of risk, profit margins are very thin. Bank loans are somewhat standard products, so it is relatively easy for customers to play one bank off against another to obtain more favourable terms. Retail banks have developed ancillary services to add value to the products that they offer to their corporate customers. Accordingly, they offer a variety of means of payment to help companies move funds efficiently from one place to another. They also help clients to manage their cash flows or their short-term investments (see Chapter 50). A retail banking division also generally includes some specific financial services for individuals (e.g. consumer credit) or for corporates (factoring, leasing, etc.), as such services are used mostly by small and medium-sized firms.
- Corporate and investment banking (CIB): provides large corporates with sophisticated services. Such banks have, at most, a few thousand clients and offer primarily the following services:
- Access to equity markets (equity capital markets, ECM): investment banks help companies prepare and carry out initial public offerings on the stock market. Later on, investment banks can continue to help these companies by raising additional funds through capital increases. They also advise companies on the issuance of instruments that may one day become shares of stock, such as warrants and convertible bonds (see Chapter 24) or the disposal of blocks of a listed subsidiary.
- Access to bond markets (debt capital markets, DCM): similarly, investment banks help large and medium-sized companies raise funds directly from investors through the issuance of bonds. The techniques of placing securities, and in particular the role of the investment bank in this type of transaction, will be discussed in Chapter 25. The investment bank’s trading room is where its role as “matchmaker” between the investor and the issuer takes on its full meaning.
- Merger and acquisition (M&A) advisory services: these investment banking services are not directly linked to corporate financing or the capital markets, although a public issue of bonds or shares often accompanies an acquisition (see Chapter 45). The first three activities are called investment banking.
- Bank financing: syndicated loans, bilateral lines, structured financing (see Chapter 21).
- Access to foreign exchange, interest rate and commodities markets: for the hedging of risk. The bank also uses these desks for speculating on its own account (see Chapter 51).
- Asset management: has its own clients – institutional investors and high-net-worth individuals – but also serves some of the retail banking clients through mutual funds. The asset management arm may sometimes use some of the products tailored by the investment banking division (hedging, order execution). This business is increasingly operated by players that are independent (totally or partially) from large banks.
Besides these global banking groups operating across all banking activities, some players have focused on certain targeted services like mergers and acquisitions and asset management (Lazard and Rothschild, for example), retail (it is the case for internet based new banks like N26, Revolut or Orange Bank) or specific geographical areas (Mediobanca and Lloyds Bank, for example).
The 2020 crisis (after 2008) demonstrated again the central role played by banks in the economy. They are suppliers of liquidity; they are also an indicator of investor risk aversion. The basic duty of a bank is to assess risk and repackage it while eliminating the diversifiable risk.
Section 15.5 THEORETICAL FRAMEWORK: EFFICIENT MARKETS
In an efficient market, prices instantly reflect the consequences of past events and all expectations about future events. As all known factors are already integrated into current prices, it is therefore impossible to predict future variations in the price of a financial instrument. Only new information will change the value of the security. Future information is, by definition, unpredictable, so changes in the price of a security are random. This is the origin of the random walk character of daily returns in the securities markets.
Competition between financial investors is so fierce that prices adjust to new information almost instantaneously. At every moment, a financial instrument trades at a price determined by its return and its risk as perceived by its investors.
Eugene Fama (1970) has developed the following three tests to determine whether a market is efficient: ability to predict future prices, market response to specific events, impact of insider information on the market.
In a weak-form efficient market, it is impossible to predict future returns. Existing prices already reflect all the information that can be gleaned from studying past prices and trading volumes. The efficient market hypothesis says that technical analysis has no practical value, nor do martingales (martingales in the ordinary, not the mathematical, sense). For example, the notion that “if a stock rises three consecutive times, buy it; if it declines two consecutive times, sell it” is irrelevant. Similarly, the efficient market hypothesis says that models relating future returns to interest rates, dividend yields, the spread between short- and long-term interest rates or other parameters are equally worthless.
A semi-strong efficient market reflects all publicly available information, as found in annual reports, newspaper and magazine articles, prospectuses, announcements of new contracts, of a merger, of an increase in the dividend, etc. This hypothesis can be empirically tested by studying the reaction of market prices to company events (event studies). In fact, the price of a stock reacts immediately to any announcement of relevant new information regarding a company. In an efficient market, no impact should be observable prior to the announcement, nor during the days following the announcement. In other words, prices should adjust rapidly only at the time any new information is announced.
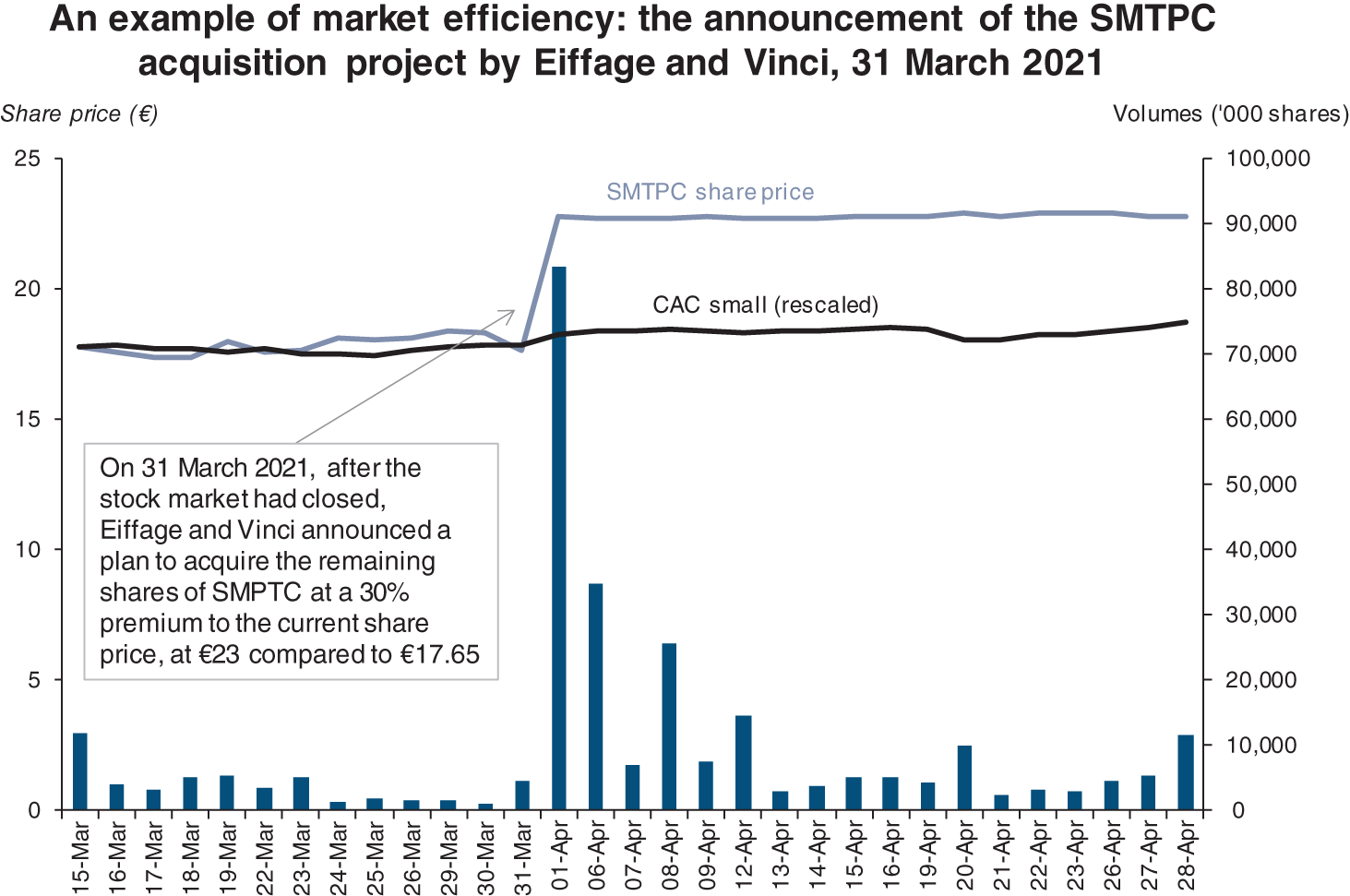
Source: Data from Euronext
In order to prevent investors with prior access to information from using it to their advantage (and therefore to the detriment of other investors), stock market regulators suggest that firms communicate before market opening or after market closure, or suspend trading prior to a mid-session announcement of information that is highly likely to have a significant impact on the share price. Trading resumes a few hours later or the following day so as to ensure that all interested parties receive the information. Then, when trading resumes, no investor has been short-changed.
In a strongly efficient financial market, investors with privileged or insider information or with a monopoly on certain information are unable to influence securities prices. This holds true only when financial market regulators have the power to prohibit and punish the use of insider information.
In theory, professional investment managers have expert knowledge that is supposed to enable them to post better performances than the market average. However, without using any inside information, the efficient market hypothesis says that market experts have no edge over the layperson. In fact, in an efficient market, the experts’ performance is slightly below the market average, in a proportion directly related to the management fees they charge!
Actual markets approach the theory of an efficient market when participants have low-cost access to all information, transaction costs are low, the market is liquid and investors are rational.
Take the example of a stock whose price is expected to rise 10% tomorrow. In an efficient market, its price will rise today to a level consistent with the expected gain. “Tomorrow’s” price will be discounted to today. Today’s price becomes an estimate of the value of tomorrow’s price.
Section 15.6 ANOTHER THEORETICAL FRAMEWORK UNDER CONSTRUCTION: BEHAVIOURAL FINANCE
Since the end of the 1960s, a large number of research papers have focused on testing the efficiency of markets. It is probably the most tested assumption of finance! Since the early 1980s, researchers (notably Thaler and Kahneman) have highlighted a number of “anomalies” that tend to go against the efficiency of markets:
- Excess volatility. The first issue with efficient market theory seems very intuitive: how can markets be so volatile? Information on Sanofi is not published every second. Nevertheless, the share price does move at each instant. There seems to be some kind of noise around fundamental value. As described by Benoit Mandelbrot, who first used fractals in economics, prices evolve in a discrete way rather than in a continuous manner.
- Dual listing and closed-end funds. Dual listings are shares of twin companies listed on two different markets. Their stream of dividends is, by definition, identical but we can observe that their price can differ over a long period of time. Similarly, the price of a closed-end fund (made up of shares of listed companies) can differ from the sum of the value of its components. Conglomerate discount (see Chapter 42) cannot explain the magnitude of the discount for certain funds and certainly not the premium for some others. It is interesting to see that these discounts can prevail over a long period of time, therefore making any arbitrage (although easy to conceptualise) hard to put in place.
- Calendar anomalies. Stocks seem to perform less well on Mondays than on other days of the week and provide higher returns in the month of January compared to other months of the year (in particular for small and medium-sized enterprises). Nevertheless, these calendar anomalies are not material enough to allow for systematic and profitable arbitrage given transaction costs. For each of these observations, some justifications consistent with the rationality of investor behaviour can be put forward.
- Meteorological anomalies. There is consistent observation that stock prices perform better when the sun shines than when it rains. There again, although statistically significant, these anomalies are not material enough to generate arbitrage opportunities.
There are some grounds to think a certain number of situations challenge the validity of the efficient market theory. Nevertheless, Eugene Fama, one of the founders of this theory, defends it strongly. He calls into question the methodologies used to find anomalies. Behavioural finance rejects the founding assumption of market efficiency: what if investors were not rational? It tries to build on other fields of social science to derive new conclusions. For example, economists will work with neuroscientists and psychologists to understand individual economic choices. This allows us to suppose that some decisions are influenced by circumstances and the environment.
One of the first tests for understanding people’s reasoning in making a choice is based on lotteries (gains with certain probabilities). The following attitudes can be observed:
- Gains and losses are not treated equally by investors: they will take risks when the probability of losing is high (they prefer a 50% chance of losing 100 to losing 50 for sure) whereas they will prefer a small gain if the probability is high (getting 50 for sure rather than a 50% chance of 100).
- If the difference (delta) in probability is narrow, the investor will choose the lottery with the highest return possible, but if the delta in probability is high, the investor will think in terms of weighted average return. This may generate some paradoxes: preferring Natixis to UBS, UBS to Mediobanca but Mediobanca to Natixis! This could drive an asset manager mad!
The lack of rationality of some investors would not be a problem if arbitrage made it possible to correct anomalies and if efficiency could be brought back rapidly. Unfortunately, anomalies can be observed over the long term.
The theory of mimicry is an illustration of behavioural finance. The economist André Orléan has distinguished three types of mimicry:
- Normative mimicry – which could also be called “conformism”. Its impact on finance is limited and is beyond the scope of this text.
- Informational mimicry – which consists of imitating others because they supposedly know more. It constitutes a rational response to a problem of dissemination of information, provided the proportion of imitators in the group is not too high. Otherwise, even if it is not in line with objective economic data, imitation reinforces the most popular choice, which can then interfere with efficient dissemination of information.
- Self-mimicry – which attempts to predict the behaviour of the majority in order to imitate it. The “right” decision then depends on the collective behaviour of all other market participants and can become a self-fulfilling prophecy, i.e. an equilibrium that exists because everyone thinks it will exist. This behaviour departs from traditional economic analysis, which holds that financial value results from real economic value.
The surge in the price of the video game company Gamestop, which went from $18 to $325 in 20 days in January 2021, or that of AMC (movie theatres), which went from $13 to $60 in the first half of 2021, are illustrations of a frenetic mimicry, totally disconnected from the economic situation, real or even possible, of these companies. These surges are rooted in the compulsive buying of tens of thousands of people who have never read a single page of the Vernimmen, or any other finance textbook, but who encourage and intoxicate each other on social networks.
Mimetic phenomena can be accentuated by program trading, which involves the computer programs used by some traders that rely on pre-programmed buy or sell decisions. These programs can schedule liquidating a position (i.e. selling an investment) if the loss exceeds a certain level. A practical issue with such programs was illustrated on 21 February 2021 by the flash crash of the bitcoin, which lost 34% before recovering its initial price in just one hour.
If some want to destroy efficient market theory, they will have to propose a viable alternative. As of today, the models proposed by “behaviourists” cannot be used, they merely model the behaviour of investors towards investment decisions and products.
Section 15.7 INVESTORS’ BEHAVIOUR
At any given point in time, each investor is either:
- a hedger;
- a speculator; or
- an arbitrageur.
1/ HEDGING
When an investor attempts to protect himself from risks they do not wish to assume, they are said to be hedging. The term “to hedge” describes a general concept that underlies certain investment decisions, for example, the decision to match a long-term investment with long-term financing, to finance a risky industrial investment with equity rather than debt, etc.
This is simple, natural and healthy behaviour for non-financial managers. Hedging protects a manufacturing company’s margin, i.e. the difference between revenue and expenses, from uncertainties in areas relating to technical expertise, human resources, sales and marketing, etc. Hedging allows the economic value of a project or line of business to be managed independently of fluctuations in the capital markets.
Accordingly, a European company that exports products to the US may sell dollars forward against euros, guaranteeing itself a fixed exchange rate for its future dollar-denominated revenues. The company is then said to have hedged its exposure to fluctuations in currency exchange rates.
2/ SPECULATION
In contrast to hedging, which eliminates risk by transferring it to a party willing to assume it, speculation is the assumption of risk. A speculator takes a position when they make a bet on the future value of an asset. If they think its price will rise, they buy it. If it rises, they win the bet; if not, they lose. If they are to receive dollars in a month’s time, they may take no action now because they think the dollar will rise in value between now and then. If they have long-term investments to make, they may finance them with short-term funds because they think that interest rates will decline in the meantime and they will be able to refinance at lower cost later. This behaviour is diametrically opposed to that of the hedger.
- Traders are professional speculators. They spend their time buying currencies, bonds, shares or options that they think will appreciate in value and they sell them when they think they are about to decline. Not surprisingly, their motto is “Buy low, sell high, play golf!”
- But the investor is also a speculator most of the time. When an investor predicts cash flows, they are speculating about the future. This is a very important point, and you must be careful not to interpret “speculation” negatively. Every investor speculates when they invest, but their speculation is not necessarily reckless. It is founded on a conviction, a set of skills and an analysis of the risks involved. The only difference is that some investors speculate more heavily than others by assuming more risk.
People often criticise the financial markets for allowing speculation. Yet speculators play a fundamental role in the market, an economically healthy role, by assuming the risks that other participants do not want to accept. In this way, speculators minimise the risk borne by others.
Accordingly, a European manufacturing company with outstanding dollar-denominated debt that wants to protect itself against exchange rate risk (i.e. a rise in the value of the dollar vs. the euro) can transfer this risk by buying dollars forward from a speculator willing to take that risk. By buying dollars forward today, the company knows the exact dollar/euro exchange rate at which it will repay its loan. It has thus eliminated its exchange rate risk. Conversely, the speculator runs the risk of a fluctuation in the value of the dollar between the time they sell the dollars forward to the company and the time they deliver them, i.e. when the company’s loan comes due.
Likewise, if a market’s long-term financing needs are not satisfied, but there is a surplus of short-term savings, then sooner or later a speculator will (fortunately) come along and assume the risk of borrowing short term in order to lend long term. In so doing, the speculator assumes intermediation risk.
What, then, do people mean by a “speculative market”? A speculative market is a market in which all the participants are speculators. Market forces, divorced from economic reality, become self-sustaining because everyone is under the influence of the same phenomenon. Once a sufficient number of speculators think that a stock will rise, their purchases alone are enough to make the stock price rise. Their example prompts other speculators to follow suit, the price rises further, and so on. But at the first hint of a downward revision in expectations, the mechanism goes into reverse and the share price falls dramatically. When this happens, many speculators will try to liquidate positions in order to pay off loans contracted to buy shares in the first place, thereby further accentuating the downfall.
3/ ARBITRAGE
In contrast to the speculator, the arbitrageur is not in the business of assuming risk or having a view on future price of an asset. Instead, they try to earn a profit by exploiting tiny discrepancies which may appear on different markets that are not in equilibrium.
An arbitrageur will notice that Solvay shares are trading slightly lower in London than in Brussels. They will buy Solvay shares in London and sell them simultaneously (or nearly so) at a higher price in Brussels. By buying in London, the arbitrageur bids the price up in London; by selling in Brussels, they drive the price down there. They, or other arbitrageurs, then repeat the process until the prices in the two markets are perfectly in line, or in equilibrium.
In principle, the arbitrageur assumes no risk, even though each separate transaction involves a certain degree of risk.
Arbitrage is of paramount importance in a market. By destroying opportunities as it uncovers them, arbitrage participates in the development of new markets by creating liquidity. It also eliminates the temporary imperfections that can appear from time to time. As soon as disequilibrium appears, arbitrageurs buy and sell assets and increase market liquidity. It is through their very actions that the disequilibrium is reduced to zero. Once equilibrium is reached, arbitrageurs stop trading and wait for the next opportunity.
Arbitrage transactions are all the faster to intervene (by computer programs nowadays) when the securities markets are liquid. Otherwise, imbalances may persist for some time on very illiquid securities. Market liquidity and progress in technology make arbitrage opportunities more and more complex and rare. Therefore, some arbitrators are forced in practice to take a certain amount of risk and therefore a speculative component normally foreign to arbitration in the pure sense of the term. In particular, the example given of Solvay is interesting to understand the concept of arbitrage but has not been relevant for quite some time.
Throughout this book, you will see that financial miracles are impossible because arbitrage levels the playing field between assets exhibiting the same level of risk.
You should also be aware that the three types of behaviour described here do not correspond to three mutually exclusive categories of investors. A market participant who is primarily a speculator might carry out arbitrage activities or partially hedge their position. A hedger might decide to hedge only part of their position and speculate on the remaining portion, etc.
The reader will not be fooled by the colloquial use of some words. “Hedge funds” do not operate hedging transactions but are most often involved in speculating. Otherwise, what explanation is there for the fact that they can earn or lose millions of dollars in a few days?
Moreover, these three types of behaviour exist simultaneously in every market. A market cannot function only with hedgers, because there will be no one to assume the risks they don’t want to take.1 As we saw above, a market composed wholly of speculators is not viable either. Finally, a market consisting only of arbitrageurs would be even more difficult to imagine.
SUMMARY
QUESTIONS
ANSWERS
BIBLIOGRAPHY
NOTES
Chapter 16. THE TIME VALUE OF MONEY AND NET PRESENT VALUE
A bird in the hand is worth two in the bush
For economic progress to be possible, in normal economic conditions, there must be a time value of money, even in a risk-free environment. This fundamental concept gives rise to the techniques of capitalisation, discounting and net present value, described below.
Section 16.1 CAPITALISATION
Consider an example of a businessman who invests €100,000 in his business at the end of 2011 and then sells it 10 years later for €1,800,000. In the meantime, he receives no income from his business, nor does he invest any additional funds into it. Here is a simple problem: given an initial outlay of €100,000 that becomes €1,800,000 in 10 years, and without any outside funds being invested in the business, what is the return on the businessman’s investment?
His profit after 10 years was €1,700,000 (€1,800,000 – €100,000) on an initial outlay of €100,000. Hence, his return was (1,700,000 / 100,000) or 1,700% over a period of 10 years.
Is this a good result or not?
Actually, the return is not quite as impressive as it first looks. To find the annual return, our first thought might be to divide the total return (1,700%) by the number of years (10) and say that the average return is 170% per year.
While this may look like a reasonable approach, it is in fact far from accurate. The value 170% has nothing to do with an annual return, which compares the funds invested and the funds recovered after one year. In the case above, there is no income for 10 years. Usually, calculating interest assumes a flow of revenue each year, which can then be reinvested, and which in turn begins producing additional interest.
There is only one sensible way to calculate the return on the above investment. First, it is necessary to seek the rate of return on a hypothetical investment that would generate income at the end of each year. After 10 years, the rate of return on the initial investment will have to have transformed €100,000 into €1,800,000. Further, the income generated must not be paid out, but rather it has to be reinvested (in which case the income is said to be capitalised).
Therefore, we are now trying to calculate the annual return on an investment that grows from €100,000 into €1,800,000 after 10 years, with all annual income to be reinvested each year.
An initial attempt to solve this problem can be made using a rate of return equal to 10%. If, at the end of 2011, €100,000 is invested at that rate, it will produce 10% × €100,000, or €10,000 in interest in 2012.
This €10,000 will then be added to the initial capital outlay and begin, in turn, to produce interest. (Hence the term “to capitalise”, which means to add to capital.) The capital thus becomes €110,000 and produces 10% × €110,000 in interest in 2013, i.e. €10,000 on the initial outlay plus €1,000 on the interest from the €10,000 interest earned in 2012 (10% × €10,000). As the interest is reinvested, the capital becomes €110,000 + €11,000, or €121,000, which will produce €12,100 in interest in 2014, and so on.
If we keep doing this until 2020, we obtain a final sum of €259,374, as shown in the table.
| Year | Capital at the beginning of the period (€) (1) | Income (€) (2) = 10% × (1) | Capital at the end of the period (€) = (1) + (2) |
|---|---|---|---|
| 2012 | 100,000 | 10,000 | 110,000 |
| 2013 | 110,000 | 11,000 | 121,000 |
| 2014 | 121,000 | 12,100 | 133,100 |
| 2015 | 133,100 | 13,310 | 146,410 |
| 2016 | 146,410 | 14,641 | 161,051 |
| 2017 | 161,051 | 16,105 | 177,156 |
| 2018 | 177,156 | 17,716 | 194,872 |
| 2019 | 194,872 | 19,487 | 214,359 |
| 2020 | 214,359 | 21,436 | 235,795 |
| 2021 | 235,795 | 23,579 | 259,374 |
Each year, interest is capitalised and itself produces interest. This is called compound interest. This is easy to express in a formula:
which can be generalised into the following:
where V is a sum and r the rate of return.
Hence, V2012 = V2011 × (1 + 10%), but the same principle can also yield:
All these equations can be consolidated into the following:
Or, more generally:
where V0 is the initial value of the investment, r is the rate of return and n is the duration of the investment in years.
This is a simple equation that gets us from the initial capital to the terminal capital. Terminal capital is a function of the rate r and the duration n.
Now it is possible to determine the annual return. In the example, the annual rate of return is not 170%, but 33.5% (which is not bad, all the same!). Therefore, 33.5% is the rate on an investment that transforms €100,000 into €1,800,000 in 10 years, with annual income assumed to be reinvested every year at the same rate.
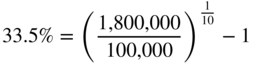
To calculate the return on an investment that does not distribute income, it is possible to reason by analogy. This is done using an investment that, over the same duration, transforms the same initial capital into the same terminal capital and produces annual income reinvested at the same rate of return. At 33.5%, annual income of €33,500 for 10 years (plus the initial investment of €100,000 paid back after the tenth year) is exactly the same as not receiving any income for 10 years and then receiving €1,800,000 in the tenth year.
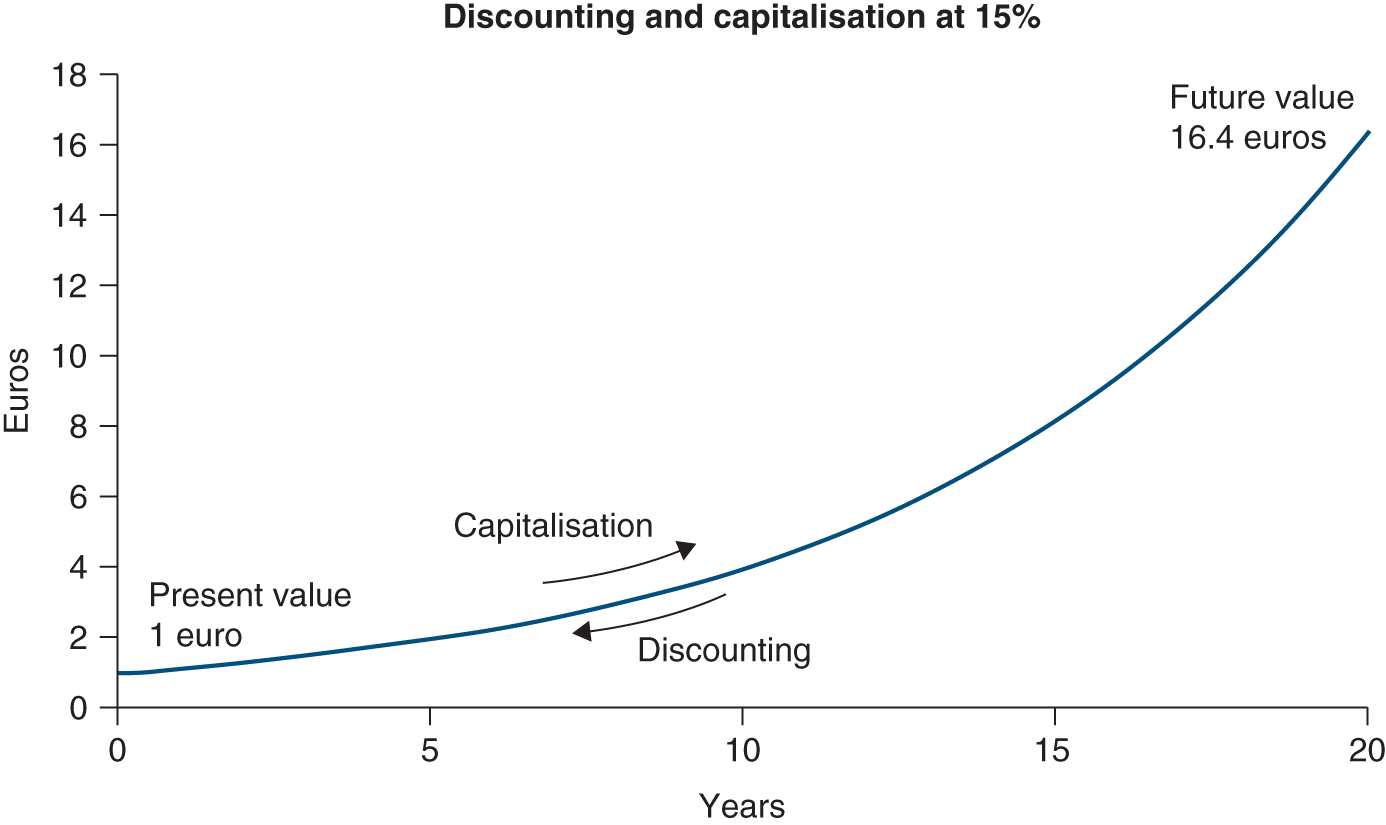
Over a long period of time, the impact of a change in the capitalisation rate on the terminal value looks as follows:
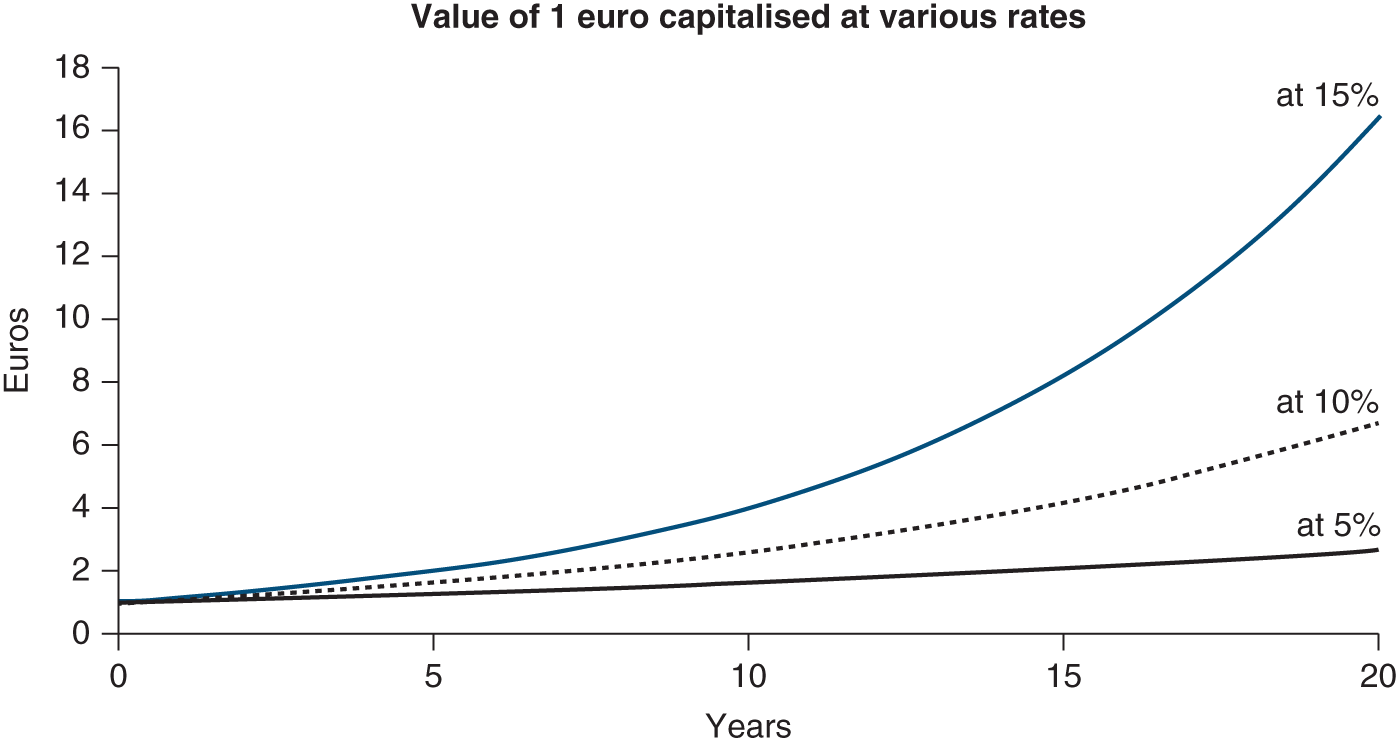
This increase in terminal value is especially important in equity valuations. The example we gave earlier of the businessman selling his company after 10 years is typical. The lower the income he has received on his investment, the more he would expect to receive when selling it. Only a high valuation would give him a return that makes economic sense.
The lack of intermediate income must be offset by a high terminal valuation. The same line of reasoning applies to an industrial investment that does not produce any income during the first few years. The longer it takes it to produce its first income, the greater that income must be in order to produce a satisfactory return.
Tripling one’s capital in 16 years, doubling it in 10 years or simply asking for a 7.177% annual return all amount to the same thing, since the rate of return is the same.
No distinction has been made in this chapter between income, reimbursement and actual cash flow. Regardless of whether income is paid out or reinvested, it has been shown that the slightest change in the timing of income modifies the rate of return.
To simplify, consider an investment of 100, which must be paid off at the end of year 1, with an interest accrued of 10. Suppose, however, that the borrower is negligent and the lender absent-minded, and the borrower repays the principal and the interest one year later than they should. The return on a well-managed investment that is equivalent to the so-called 10% on our absent-minded investor’s loan can be expressed as:
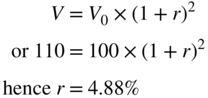
This return is less than half of the initially expected return!
It is not accounting and legal appearances that matter, but rather actual cash flows.
Section 16.2 DISCOUNTING
1/ WHAT DOES IT MEAN TO DISCOUNT A SUM?
Discounting into today’s euros helps us compare a sum that will not be produced until later. Technically speaking, what is discounting?
To discount is to “depreciate” the future. It is to be more rigorous with future cash flows than present cash flows, because future cash flows cannot be spent or invested immediately. First, take tomorrow’s cash flow and then apply to it a multiplier coefficient below 1, which is called a discounting factor. The discounting factor is used to express a future value as a present value, thus reflecting the depreciation brought on by time.
Consider an offer whereby someone will give you €1,000 in five years. As you will not receive this sum for another five years, you can apply a discounting factor to it, for example, 0.6. The present, or today’s, value of this future sum is then 600. Having discounted the future value to a present value, we can then compare it to other values. For example, it is preferable to receive 650 today rather than 1,000 in five years, as the present value of 1,000 five years out is 600, and that is below 650.
Remember that investors discount becausethey demand a certain rate of return. If a security pays you 110 in one year and you wish to see a return of 10% on your investment, the most you would pay today for the security (i.e. its present value) is 100. At this price (100) and for the amount you know you will receive in one year (110), you will get a return of 10% on your investment of 100. However, if a return of 11% is required on the investment, then the price you are willing to pay changes. In this case, you would be willing to pay no more than 99.1 for the security because the gain would have been 10.9 (or 11% of 99.1), which will still give you a final payment of 110.
Discounting converts a future value into a present value. This is the opposite result of capitalisation.
Discounting converts future values into present values, while capitalisation converts present values into future ones. Hence, to return to the example above, €1,800,000 in 10 years discounted at 33.5% is today worth €100,000. €100,000 today will be worth €1,800,000 when capitalised at 33.5% over 10 years.
2/ DISCOUNTING AND CAPITALISATION FACTORS
To discount a sum, the same mathematical formulas are used as those for capitalising a sum. Discounting calculates the sum in the opposite direction to capitalising.
To get from €100,000 today to €1,800,000 in 10 years, we multiply 100,000 by (1 + 0.335)10, or 18. The number 18 is the capitalisation factor.
To get from €1,800,000 in 10 years to its present value today, we would have to multiply €1,800,000 by 1 / (1 + 0.335)10, or 0.056. 0.056 is the discounting factor, which is the inverse of the coefficient of capitalisation. The present value of €1,800,000 in 10 years at a 33.5% rate is €100,000.
More generally:
which is the exact opposite of the capitalisation formula.
1 / (1 + r)n is the discounting factor, which depreciates Vn and converts it into a present value V0. It is most often below 1, as discounting rates are generally positive.
Section 16.3 PRESENT VALUE AND NET PRESENT VALUE OF A FINANCIAL SECURITY
Owning a financial security such as a stock or a bond means owning the right to receive cash flows (dividend, interest, reimbursement, etc.) according to the specific terms of the security.
1/ FROM THE PRESENT VALUE OF A SECURITY …
The present value (PV) of a security is the sum of its discounted cash flows, i.e.:
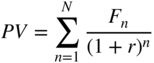
where Fn are the cash flows generated by the security, r is the applied discounting rate and n is the number of years for which the security is discounted.
All securities also have a market value, particularly on the secondary market. Market value is the price at which a security can be bought or sold.
Net present value (NPV) is the difference between present value and market value (V0):
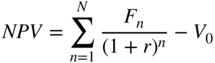
If the net present value of a security is greater than its market value, then it will be worth more in the future than the market has presently valued it at. Therefore, you will probably want to invest in it, i.e. to invest in the upside potential of its value.
If, however, the security’s present value is below its market value, then you should sell it at once (as its net present value is negative), for its market value is sure to diminish.
2/ … TO ITS FAIR VALUE
If an imbalance occurs between a security’s market value and its present value, then efficient markets will seek to re-establish balance and reduce net present value to zero. Investors acting on efficient markets seek out investments offering positive net present value, in order to realise that value. When they do so, they push net present value towards zero, ultimately arriving at the fair value of the security.
3/ APPLYING THE CONCEPT OF NET PRESENT VALUE TO OTHER INVESTMENTS
Up to this point, the discussion has been limited to financial securities. However, the concepts of present value and net present value can easily be applied to any investment, such as the construction of a new factory, the launch of a new product, the takeover of a competing company or any other asset that will generate positive and/or negative cash flows.
The concept of net present value can be interpreted in three different ways:
- The value created by an investment – for example, if the investment requires an outlay of €100 and the present value of its future cash flow is €110, then the investor has become €10 wealthier.
- The maximum additional amount that the investor is willing to pay to make the investment – if the investor pays up to €10 more, they have not necessarily made a bad deal, as they are paying up to €110 for an asset that is worth €110.
- The difference between the present value of the investment (€110) and its market value (€100).
Section 16.4 WHAT DOES NET PRESENT VALUE DEPEND ON?
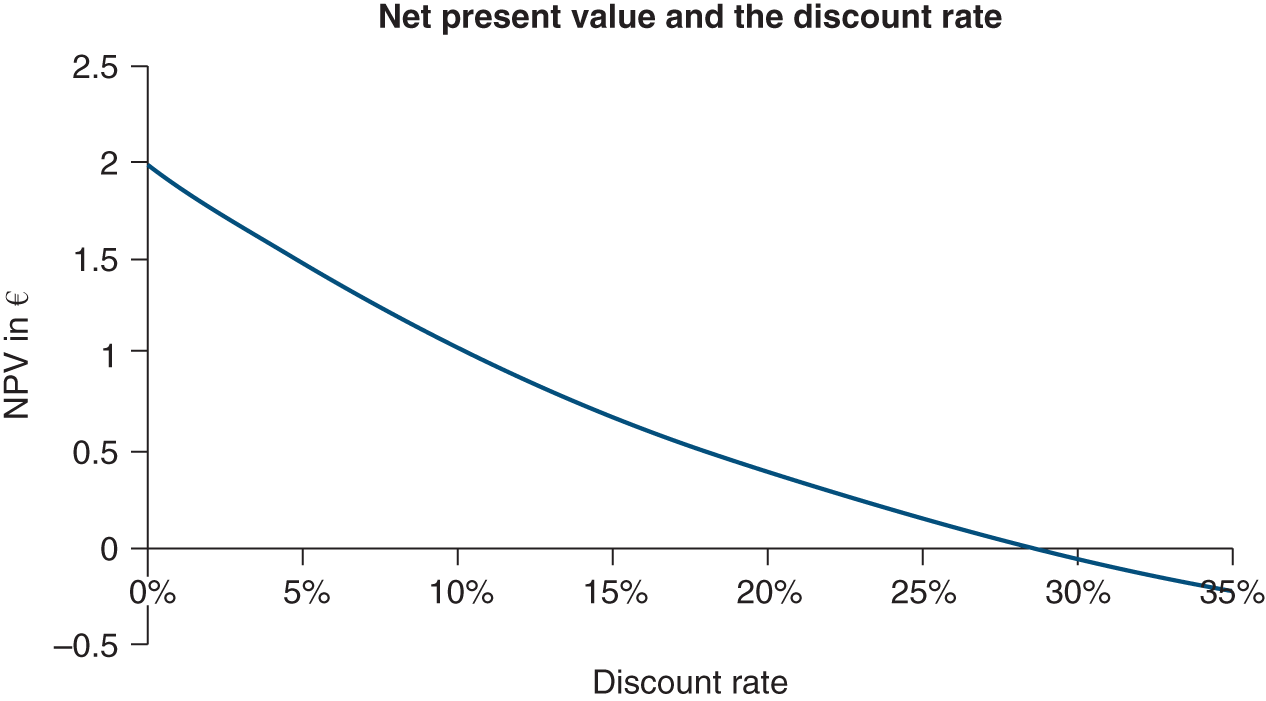
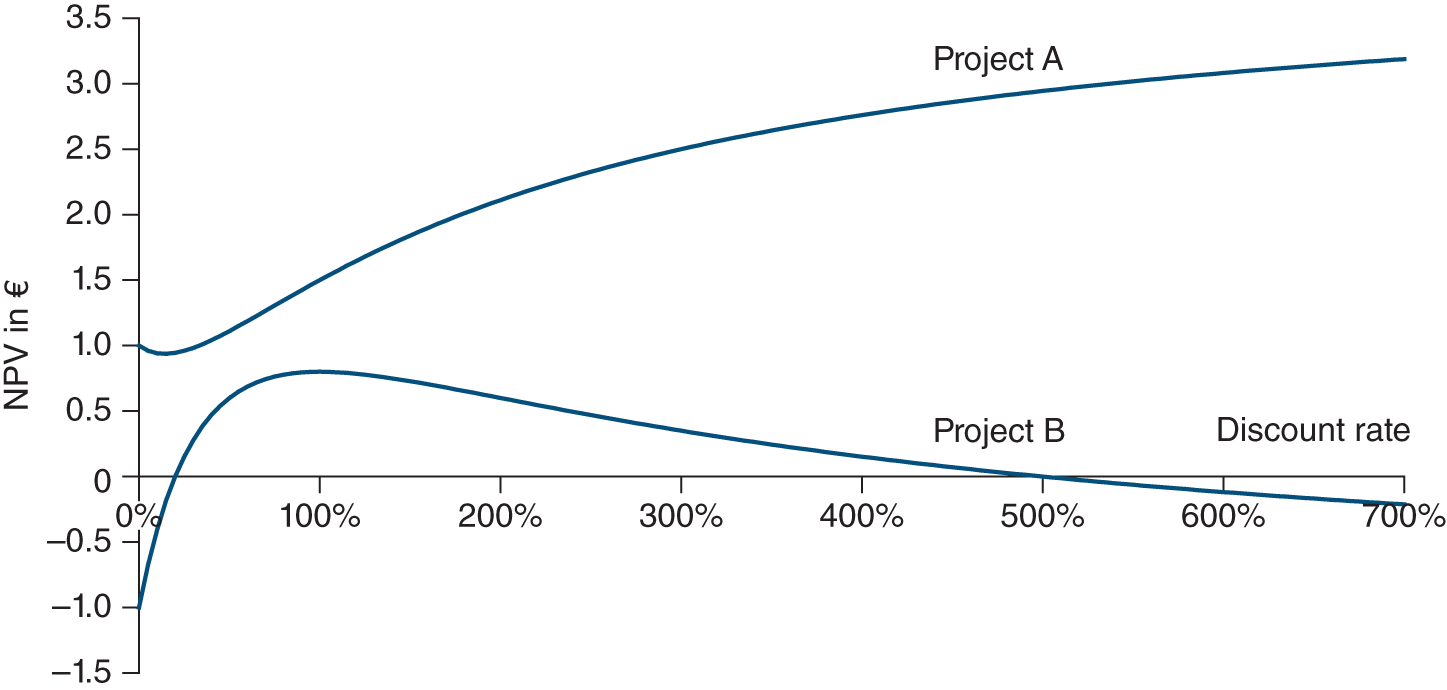
While net present value is obviously based on the amount and timing of cash flows, it is worth examining how it varies with the discounting rate.
The higher the discounting rate, the more future cash flow is depreciated and, therefore, the lower is the present value. Net present value declines in inverse proportion to the discounting rate, thus reflecting investor demand for a greater return (i.e. greater value attributed to time).
Take the following example of an asset (e.g. a financial security or a capital investment) with a market value of 2 and with cash flows as follows:
| Year | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Cash flow | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
A 20% discounting rate would produce the following discounting factors:
| Year | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Discounting factor | 0.833 | 0.694 | 0.579 | 0.482 | 0.402 |
| Present value of cash flow | 0.67 | 0.56 | 0.46 | 0.39 | 0.32 |
As a result, the present value of this investment is 2.40.1 As its market value is 2, its net present value is 0.40.
If the discounting rate changes, the following values are obtained:
| Discounting rate | 0% | 10% | 20% | 25% | 30% | 35% |
|---|---|---|---|---|---|---|
| Present value of the investment | 4 | 3.03 | 2.39 | 2.15 | 1.95 | 1.78 |
| Market value | 2 | 2 | 2 | 2 | 2 | 2 |
| Net present value | 2 | 1.03 | 0.39 | 0.15 | −0.05 | −0.22 |
Which would then look like this graphically:
Section 16.5 SOME EXAMPLES OF SIMPLIFICATION OF PRESENT VALUE CALCULATIONS
For those occasions when you are without your favourite spreadsheet program, you may find the following formulas handy in calculating present value.
1/ THE VALUE OF AN ANNUITY F OVER N YEARS, BEGINNING IN YEAR 1
or:
For the two formulas above, the sum of the geometric series can be expressed more simply as:
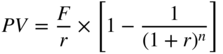
So, if F = 0.8, r = 20% and n = 5, then the present value is indeed 2.4.
Further, ![]() is equal to the sum of the first n discounting factors.
is equal to the sum of the first n discounting factors.
2/ THE VALUE OF A PERPETUITY
A perpetuity is a constant stream of cash flows without end. By adding this feature to the previous case, the formula then looks like this:
As n approaches infinity in the formula of the previous paragraph, this can be shortened to the following:
The present value of a €100 perpetuity discounted back at 10% per year is thus:
A €100 perpetuity discounted at 10% is worth €1,000 in today’s euros. If the investor demands a 20% return, then the same perpetuity is worth €500.
3/ THE VALUE OF AN ANNUITY THAT GROWS AT RATE G FOR N YEARS
In this case, the F0 cash flow rises annually by g for n years.
Thus:
or:
Note: the first cash flow actually paid out is F0 × (1 + g).
Thus, a security that has just paid out 0.8, and with this 0.8 growing by 10% each year for the four following years, has – at a discounting rate of 20% – a present value of:
4/ THE VALUE OF A PERPETUITY THAT GROWS AT RATE G (GROWING PERPETUITY)
As n approaches infinity, the previous formula can be expressed as follows:
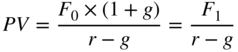
As long as r > g. The present value is thus equal to the next year’s cash flow divided by the difference between the discounting rate and the annual growth rate.
For example, a security with an annual return of 0.8, growing by 10% annually to infinity, has, at a rate of 20%, PV = 0.8 / (0.2 – 0.1) = 8.0.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTE
Chapter 17. THE INTERNAL RATE OF RETURN
A well-deserved return
If net present value (NPV) is inversely proportional to the discounting rate, then there must exist a discounting rate that makes NPV equal to zero.
To apply this concept to capital expenditure, simply replace “yield to maturity” by “IRR”, as the two terms mean the same thing. It is just that one is applied to financial securities (yield to maturity) and the other to capital expenditure (IRR).
Section 17.1 CALCULATING YIELD TO MATURITY
To calculate yield to maturity, make r the unknown and simply use the NPV formula again. The rate r is determined as follows:
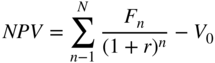
To use the same example from Section 16.4:
In other words, an investment’s yield to maturity is the rate at which its market value is equal to the present value of the investment’s future cash flows.
In our illustration, the IRR is about 28.6% (see figure in Section 16.4).
Section 17.2 YIELD TO MATURITY AS AN INVESTMENT CRITERION
The yield to maturity is frequently used in financial markets because it represents for the investor the return to be expected for a given level of risk, which they can then compare to their required return rate, thereby simplifying the investment decision.
The decision-making rule is very simple: if an investment’s yield to maturity is higher than the investor’s required return, they will make the investment or buy the security. Otherwise, they will abandon the investment or sell the security.
In our example, since the yield to maturity (28.6%) is higher than the return demanded by the investor (20%), they should make the investment. If the market value of the same investment were 3 (and not 2), the yield to maturity would be 10.4%, and they should not invest.
Hence, at fair value, the yield to maturity is identical to the market’s required return. In other words, net present value is nil (this will be developed further in Chapter 26).
Section 17.3 THE LIMITS OF YIELD TO MATURITY OR IRR
With this new investment-decision-making criterion, it is now necessary to consider how IRR can be used vis-à-vis net present value. It is also important to investigate whether or not these two criteria could somehow produce contradictory conclusions.
If it is a simple matter of whether or not to buy into a given investment, or whether or not to invest in a project, then the two criteria produce exactly the same result, as shown in the example.
If the cash flow schedule is the same, then calculating the NPV by choosing the discounting rate and calculating the internal rate of return (and comparing it with the discounting rate) are two sides of the same mathematical coin.
The issue is, however, a bit more complex when it comes to choosing between several securities or projects, which is usually the case. Comparing several streams of cash flows (securities) should make it possible to choose between them.
1/ THE REINVESTMENT RATE AND THE MODIFIED IRR (MIRR)
Consider two investments A and B, with the following cash flows:
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Investment A | 6 | 0.5 | |||||
| Investment B | 2 | 3 | 0 | 0 | 2.1 | 0 | 5.1 |
At a 5% discount rate, the present value of investment A is 6.17 and that of investment B is 9.90. If investment A‘s market value is 5, its net present value is 1.17. If investment B‘s market value is 7.5, its net present value is 2.40.
Now calculate the IRR. It is 27.8% for investment A and 12.7% for investment B. Or, to sum up:
| NPV at 5% | IRR% | |
|---|---|---|
| Investment A | 1.17 | 27.8 |
| Investment B | 2.40 | 12.7 |
Investment A delivers a rate of return that is much higher than the required return (27.8% vs. 5%) during a short period of time. Investment B‘s rate of return is much lower (12.7% vs. 27.8%), but is still higher than the 5% required return demanded and is delivered over a far longer period (seven years vs. two). Our NPV and internal rate of return models are telling us two different things. So, should we buy investment A or investment B?
At first glance, investment B would appear to be the more attractive of the two. Its NPV is higher and it creates the most value: 2.40 vs. 1.17.
However, some might say that investment A is more attractive, as cash flows are received earlier than with investment B and therefore can be reinvested sooner in high-return projects. While that is theoretically possible, it is the strong (and optimistic) form of the theory because competition among investors and the mechanisms of arbitrage tend to move net present values towards zero. Net present values moving towards zero means that exceptional rates of return converge towards the required rate of return, thereby eliminating the possibility of long-lasting high-return projects.
Given the convergence of the exceptional rates towards required rates of return, it is more reasonable to suppose that cash flows from investment A will be reinvested at the required rate of return of 5%. The exceptional rate of 27.8% is unlikely to be recurrent.
And this is exactly what happens if we adopt the NPV decision rule. The NPV in fact assumes that the reinvestment of interim cash flows is made at the required rate of return. The IRR assumes that the reinvestment rate of interim cash flows is simply the IRR itself. However, in equilibrium, it is unreasonable to think that the company can continue to invest at the same rate of the (sometimes) exceptional IRR of a specific project. Instead, it is much more reasonable to assume that, at best, the company can invest at the required rate of return.
However, a solution to the reinvestment rate problem of IRR is the modified IRR (MIRR).
So, by capitalising cash flow from investments A and B at the required rate of return (5%) up to period 7, we obtain from investment A in period 7: 6 × 1.0056 + 0.5 × 1.055, or 8.68. From investment B we obtain 2 × 1.056 + 3 × 1.055 + 2.1 × 1.052 + 5.1, or 13.9. The internal rate of return that allows for investment A in capitalising over seven years to reach 8.68 is 8.20%; it is often called modified IRR. For investment B, the modified IRR is 9.24%.
We have thus reconciled the NPV and internal rate of return models.
Some might say that it is not consistent to expect investment A to create more value than investment B, as only 5 has been invested in A vs. 7.5 for B. Even if we could buy an additional “half-share” of A, in order to equalise the purchase price, the NPV of our new investment in A would only be 1.17 × 1.5 = 1.76, which would still be less than investment B‘s NPV of 2.40. For the reasons discussed above, we are unlikely to find another investment with a return identical to that of investment A.
Instead, we should assume that the 2.5 in additional investment would produce the required rate of return (5%) for seven years. In this case, NPV would remain, by definition, at 1.17, whereas the internal rate of return of this investment would fall to 11%. NPV and the internal rate of return would once again lead us to conclude that investment B is the more attractive investment.
In fact, the NPV criterion is a better choice criterion than the IRR because it assumes that the intermediate flows of the investment are reinvested at the required rate of return (the discount rate), whereas in the calculation of the IRR they are assumed to be reinvested at that rate. The latter assumption is very strong because, if the IRR is higher than the required rate of return, it assumes that the company will always find projects that yield more than the required rate of return.
2/ MULTIPLE OR NO IRR
Finally, there are some rare cases where the use of the IRR leads to a deadlock. Consider the following investments:
| Year | 0 | 1 | 2 |
|---|---|---|---|
| Project A | 4 | −7 | 4 |
| Project B | −1 | 7.2 | −7.2 |
Project A has no IRR. Thus, we have no benchmark for deciding if it is a good investment or not. Although the NPV remains positive for all the discount rates, it remains only slightly positive and the company may decide not to do it.
Project B has two IRRs, and we do not know which is the right one. There is no good reason to use one over the other. Investments with “unconventional” cash flow sequences are rare, but they can happen. Consider a firm that is cutting timber in a forest. The timber is cut, sold and the firm gets an immediate profit. But, when harvesting is complete, the firm may be forced to replant the forest at considerable expense.
The IRR criterion does not allow for the ranking of different investment opportunities. It only allows us to determine whether one project yields at least the return required by investors. When the IRR does not allow us to judge whether an investment project should be undertaken or not (e.g. no IRR or several IRRs), the NPV should be analysed.
Section 17.4 EFFECTIVE ANNUAL RATE, NOMINAL RATES AND PROPORTIONAL RATES
We have just discovered the IRR, but many readers will be more aware of the interest rate, especially those planning to take out a loan. How can we reconcile the two?
Consider someone who wants to lend you €1,000 today at 10% for four years. This 10% means 10% per year and constitutes the nominal rate of return of your loan. This rate will be the basis for calculating interest, proportional to the time elapsed and the amount borrowed. Assume that you will pay interest annually, at the end of each annual period rather than at the beginning.
1/ THE CONCEPT OF EFFECTIVE ANNUAL RATE
Now what happens when interest is paid not once but several times per year?
Suppose that somebody lends you money at 10% but says (somewhere in the fine print at the bottom of the page) that interest will have to be paid on a half-yearly basis. For example, suppose you borrowed €100 on 1 January and then had to pay €5 in interest on 1 July and €5 on 1 January of the following year, as well as the €100 in principal at the same date.
This is not the same as borrowing €100 and repaying €110 one year later. The amount of interest may be the same (5 + 5 = 10), but the payment schedule is not. In the first case, you will have to pay €5 on 1 July (just before leaving on summer holiday), which you could have kept until the following 1 January in the second case. In the first case you pay €5, instead of investing it for six months as you could have done in the second case.
As a result, the loan in the first case costs more than a loan at 10% with interest due annually. Its effective rate is not 10%, since interest is not being paid on the benchmark annual terms.
To avoid comparing apples and oranges, a financial officer must take into account the effective date of disbursement. We know that one euro today is not the same as one euro tomorrow. Obviously, the financial officer wants to postpone expenditure and accelerate receipts, thereby having the money work for them. So, naturally, the repayment schedule matters when calculating the rate.
Which is the best approach to take? If the interest rate is 10%, with interest payable every six months, then the interest rate is 5% for six months. We then have to calculate an effective annual rate (and not for six months), which is our point of reference and our constant concern.
Two rates referring to two different maturities are said to be equivalent if the future value of the same amount at the same date is the same with the two rates.
In our example, the lender receives €5 on 1 July which, compounded over six months, becomes 5 + (10% × 5) / 2 = €5.25 on the following 1 January, the date on which they receive the second €5 interest payment. So, over one year, they will have received €10.25 in interest on a €100 investment.
Therefore, the effective annual rate is 10.25%. This is the real cost of the loan, since the return for the lender is equal to the cost for the borrower.
If the apparent rate (or nominal rate) (ra) is to be paid n times per year, then the effective annual rate (t) is obtained by compounding this nominal rate n times after first dividing it by n:
where n is the number of interest payments in the year and ra / n the proportional rate during one period, or t = (1 + ra / n)n − 1.
In our example:
The effective interest rate is thus 10.25%, while the nominal rate is 10%.
It should be common sense that an investment at 10% paying interest every six months produces a higher return at year end than an investment paying interest annually. In the first case, interest is compounded after six months and thus produces interest on interest for the next six months. Obviously, a loan on which interest is due every six months will cost more than one on which interest is charged annually.
The table below gives the returns produced by an investment (a loan) at 10% with varying instalment frequencies:
The effective annual rate can be calculated on any timescale. For example, a financial officer might wish to use continuous rates. This might mean, for example, a 10% rate producing €100, paid out evenly throughout the year on a principal of €1,000. As long as the financial officer is familiar with a rate corresponding to interest paid once a year, they will keep this rate as a reference rate.
By definition, IRR and yields to maturity are effective annual rates.
2/ THE CONCEPT OF PROPORTIONAL RATE
In our example of a loan at 10%, we would say that the 5% rate over six months is proportional to the 10% rate over one year. More generally, two rates are proportional if they are in the same proportion to each other as the periods to which they apply.
For example, 10% per year is proportional to 5% per half-year or 2.5% per quarter, but 5% half-yearly is not equivalent to 10% annually. Effective annual rate and proportional rates are therefore two completely different concepts that should not be confused.
Proportional rates serve only to simplify calculations, but they hide the true cost of a loan. Only the effective annual rate (10.25%/year) gives the true cost, unlike the proportional rate (10%/year).
When the time span between two interest payment dates is less than one year, the proportional rate is lower than the effective annual rate (10% is less than 10.25%). When maturity is more than a year, the proportional rate overestimates the effective annual rate. This is rare, whereas the first case is quite frequent on money markets, where money is lent or borrowed for short periods of time.
As we will see, the bond market practice can be misleading for the investor focusing on par value: bonds are sold above or below par value, the number of days used in calculating interest can vary, bonds may be repaid above par value, and so on. And, most importantly, on the secondary market, a bond’s present value depends on fluctuations in market interest rates.
Section 17.5 SOME MORE FINANCIAL MATHEMATICS: LOAN REPAYMENT TERMS
The first problem is how and when will you pay off the loan?
Repayment terms constitute the method of amortisation of the loan. Take the following examples.
1/ BULLET REPAYMENT
The entire loan is paid back at maturity.
The cash flow table would look like this:
| Period | Principal still due | Interest | Amortisation of principal | Annuity |
|---|---|---|---|---|
| 1 | 1,000 | 100 | 0 | 100 |
| 2 | 1,000 | 100 | 0 | 100 |
| 3 | 1,000 | 100 | 0 | 100 |
| 4 | 1,000 | 100 | 1,000 | 1,100 |
Total debt service is the annual sum of interest and principal to be paid back. This is also called debt servicing at each due date.
2/ CONSTANT (OR LINEAR) AMORTISATION
Each year, the borrower pays off a constant proportion of the principal, corresponding to 1/n, where n is the initial maturity of the loan.
The cash flow table would look like this:
| Period | Principal still due | Interest | Amortisation of principal | Annuity |
|---|---|---|---|---|
| 1 | 1,000 | 100 | 250 | 350 |
| 2 | 750 | 75 | 250 | 325 |
| 3 | 500 | 50 | 250 | 300 |
| 4 | 250 | 25 | 250 | 275 |
3/ EQUAL INSTALMENTS
The borrower may want to allocate a fixed sum to the service of debt (capital repayment and interests).
Based on the discounting method described previously, consider a constant annuity A, such that the sum of the four discounted annuities is equal to the present value of the principal, or €1,000:
This means that the NPV of the 10% loan is nil; in other words, the 10% nominal rate of interest is also the internal rate of return of the loan.
Using the formula from Section 16.5, paragraph 1, the previous formula can be expressed as follows:
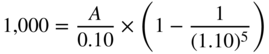
A = €315.47. Hence, the following repayment schedule:
| Period | Principal still due | Interest | Amortisation of principal | Annuity |
|---|---|---|---|---|
| 1 | 1,000 | 100 | 215.47 | 315.47 |
| 2 | 784.53 | 78.45 | 237.02 | 315.47 |
| 3 | 547.51 | 54.75 | 260.72 | 315.47 |
| 4 | 286.79 | 28.68 | 286.79 | 315.47 |
In this case, the interest for each period is indeed equivalent to 10% of the remaining principal (i.e. the nominal rate of return) and the loan is fully paid off in the fourth year. Internal rate of return and nominal rate of interest are identical, as calculation is on an annual basis and the repayment of principal coincides with the payment of interest.
Regardless of which side of the loan you are on, both work the same way. We start with invested (or borrowed) capital, which produces income (or incurs interest costs) at the end of each period. Eventually, the loan is then either paid back (leading to a decline in future revenues or in interest to be paid) or held on to, thus producing a constant flow of income (or a constant cost of interest).
4/ INTEREST AND PRINCIPAL BOTH PAID WHEN THE LOAN MATURES
In this case, the borrower pays nothing until the loan matures. The sum that the borrower will have to pay at maturity is none other than the future value of the sum borrowed, capitalised at the interest rate of the loan:
This is how the repayment schedule would look:
| Period | Principal and interest still due | Amortisation of principal | Interest payments | Annuity |
|---|---|---|---|---|
| 1 | 1,000 | 0 | 0 | 0 |
| 2 | 1,100 | 0 | 0 | 0 |
| 3 | 1,219 | 0 | 0 | 0 |
| 4 | 1,331 | 1,331 | 1,331 | 1,464.1 |
This is a zero-coupon loan.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTE
****PART TWO. THE RISK OF SECURITIES AND THE REQUIRED RATE OF RETURN
After having covered the basics of finance (discounting, capitalisation, value and interest rates), it is time to delve deeper into another fundamental concept: risk. Risk is the uncertainty over future asset values and future returns. For better or for worse, without risk, finance would be quite boring!
Risk means uncertainty today over the cash flows and value of an asset tomorrow. Of course, it is possible to review all the factors that could have a negative or positive impact on an asset, quantify each one and measure the total impact on the asset’s value. In reality, it is infinitely more practical to boil all the risks down to a single figure.
Chapter 18. RISK AND RETURN
The spice of finance
Investors who buy financial securities face risks because they do not know with certainty the future selling price of their securities, nor the cash flows they will receive in the meantime. This chapter will try to explain and measure this risk, and also examine its repercussions.
Section 18.1 SOURCES OF RISK
There are various risks involved in financial securities, including:
- Industrial, commercial and labour risks, etc.
There are so many types of risk in this category that we cannot list them all here. They include lack of competitiveness, emergence of new competitors, technological breakthroughs, an inadequate sales network, strikes and so on. These risks tend to lower cash flow expectations and thus have an immediate impact on the value of the stock.
- Liquidity risk
This is the risk of not being able to sell an asset at its fair value as a result of either a liquidity discount or the complete absence of a market or buyers.
- Credit risk
This is the risk that a creditor will lose their entire investment if a debtor cannot repay them in full, even if the debtor’s assets are liquidated. Traders call this counterparty risk.
- Foreign exchange (FX) risk
Fluctuations in exchange rates can lead to a loss of value of assets denominated in foreign currencies. Similarly, higher exchange rates can increase the value of debt denominated in foreign currencies when translated into the company’s reporting currency base.
- Interest rate risk
The holder of financial securities is exposed to the risk of interest rate fluctuations. Even if the issuer fulfils their commitments entirely, there is still the risk of a capital loss or, at the very least, an opportunity loss.
- Systemic risk
This is the risk of collapse of the overall financial system through the bankruptcy chain and the domino effect linked to the interdependency of market players.
- Political risk
This includes risks created by a particular political situation or decisions by political authorities, such as nationalisation without sufficient compensation, revolution, exclusion from certain markets, discriminatory tax policies, inability to repatriate capital, etc.
- Regulatory risk
A change in the law or in regulations can directly affect the return expected in a particular sector. Pharmaceuticals, banks and insurance companies, among others, tend to be on the front lines here.
- Inflation risk
This is the risk that the investor will recover their investment with a depreciated currency, i.e. that they will receive a return below the inflation rate. A flagrant historical example is the hyperinflation in Germany in the 1920s.
- The risk of a fraud
This is the risk that some parties (internal or external) will lie or cheat. The most common examples are insider trading, CEO fraud or ransomware.
- Natural disaster risks
These include storms, earthquakes, volcanic eruptions, cyclones, tidal waves, etc., which destroy assets, or of a pandemic that stops the activity or restrains it a lot. The recent past has demonstrated that those risks cannot be neglected.
- Economic risk
This type of risk is characterised by bull or bear markets, anticipation of an acceleration or a slowdown in business activity or changes in labour productivity.
The list is nearly endless; however, at this point it is important to highlight two points:
- most financial analysis mentioned and developed in this book tends to generalise the concept of risk and highlight its impact on valuations, rather than analysing it in depth. So, given the extent to which markets are efficient and evaluate risk correctly, it is not necessary to redo what others have already done; and
- risk is always present. The so-called risk-free rate, to be discussed later, is simply a manner of speaking. Risk is always present, and to say that risk can be eliminated is either to be excessively confident or to be unable to think about the future – both very serious faults for an investor.
Obviously, any serious investment study should begin with a precise analysis of the risks involved.
The knowledge gleaned from analysts with extensive experience in the business, mixed with common sense, allows us to classify risks into two categories:
- economic risks (political, natural, inflation, fraud and other risks), which threaten cash flows from investments and which come from the “real economy”; and
- financial risks (liquidity, currency, interest rate and other risks), which do not directly affect cash flow, but nonetheless do come into the financial sphere. These risks are due to external financial events, and not to the nature of the issuer.
Section 18.2 RISK AND FLUCTUATION IN THE VALUE OF A SECURITY
All of the aforementioned risks can penalise the financial performance of companies and their future cash flows. Obviously, if a risk materialises that seriously hurts company cash flows, then investors will seek to sell their securities. Consequently, the value of the security falls.
Moreover, if a company is exposed to significant risk, then some investors will be reluctant to buy its securities. Even before risk materialises, investors’ perceptions that a company’s future cash flows are uncertain or volatile will serve to reduce the value of its securities.
Most modern finance is based on the premise that investors seek to reduce the uncertainty of their future cash flows. By its very nature, risk increases the uncertainty of an asset’s future cash flow, and it therefore follows that such uncertainty will be priced into the market value of a security.
Investors consider risk only to the extent that it affects the value of the security. Risks can affect value by changing anticipations of cash flows or the rate at which these cash flows are discounted.
To begin with, it is important to realise that in corporate finance no fundamental distinction is made between the risk of asset revaluation and the risk of asset devaluation.
That is to say, whether investors expect the value of an asset to rise (upside) or decrease (downside) is immaterial.1 It is the fact that risk exists in the first place that is of significance and affects how investors behave.
Consider, for example, a security with the following cash flows expected for years 1 to 4:
| Year | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Cash flow (in €) | 100 | 120 | 150 | 190 |
Imagine the value of this security is estimated to be €2,000 in five years. Assuming a 9% discounting rate, its value today would be:
If a sudden sharp rise in interest rates raises the discounting rate to 13%, the value of the security becomes:
The security’s value has fallen by 15% whereas cash flows have not changed.
However, if the company comes out with a new product that raises projected cash flow by 20%, with no further change in the discounting rate, the security’s value then becomes:
The security’s value increases for reasons specific to the company, not because of a fall of interest rates in the market.
Now, suppose that there is an improvement in the overall economic outlook that lowers the discounting rate to 10%. If there is no change in expected cash flows, the stock’s value would be:
Again, there has been no change in the stock’s intrinsic characteristics and yet its value has risen by 12%.
If there is stiff price competition, then previous cash flow projections will have to be adjusted downward by 10%. If all cash flows fall by the same percentage and the discounting rate remains constant, the value of the company becomes:
Once again, the security’s value decreases for reasons specific to the company, not because of a fall in the market.
In the previous example, a European investor would have lost 10% of their investment (from €2,009 to €1,808). If, in the interim, the euro had risen from $1.10 to $1.31, a US investor would have gained 7% (from $2,210 to $2,365).
A closer analysis shows that some securities are more volatile than others, i.e. their price fluctuates more widely. We say that these stocks are “riskier”. The riskier a stock is, the more volatile its price, and vice versa. Conversely, the less risky a security is, the less volatile its price, and vice versa.
Volatility can be measured mathematically by variance and standard deviation.
Typically, it is safe to assume that risk dissipates over the long term. The erratic fluctuations in the short term give way to the clear outperformance of equities over bonds, and bonds over money-market investments. The chart below tends to back up this point of view. It presents data on the path of wealth (POW) for the three asset classes. The POW measures the growth of €1 invested in any given asset, assuming that all proceeds are reinvested in the same asset.
As is easily seen from the chart, risk does dissipate, but only over the long term. In other words, an investor must be able to invest their funds and then do without them during this long-term timeframe. It sometimes requires strong nerves not to give in to the temptation to sell when prices collapse, as happened with stock markets in 1929, 1974, 2001, 2008, or 2011.
Since 1900, UK stocks have delivered an average annual return after inflation of 5.4%. Yet, during 39 of those years the returns were negative, in particular in 1974, when investors lost 57% on a representative portfolio of UK stocks.
Source: Data from Factset
Source: Based on Dimson, Marsh and Staunton (2020)
And in worst-case scenarios, it must not be overlooked that some financial markets vanished entirely, including the Russian equity market after the 1917 revolution, the German bond market with the hyperinflation of 1921–1923, the Japanese and German equity markets in 1945, and the Chinese equity market in 1949. Over the stretch of one century, these may be exceptional events, but they have enormous repercussions when they do occur.
Section 18.3 TOOLS FOR MEASURING RETURN AND RISK
1/ EXPECTED RETURN
To begin, it must be realised that a security’s rate of return and the value of a financial security are actually two sides of the same coin. The rate of return will be considered first.
The holding-period return is calculated from the sum total of cash flows for a given investment, i.e. income, in the form of interest or dividends earned on the funds invested and the resulting capital gain or loss when the security is sold.
If just one period is examined, then the return on a financial security can be expressed as follows:
Here, F1 is the income received by the investor during the period, V0 is the value of the security at the beginning of the period and V1 is the value of the security at the end of the period.
In an uncertain world, investors cannot calculate their returns in advance, as the value of the security is unknown at the end of the period. In some cases, the same is true for the income to be received during the period.
Therefore, investors use the concept of expected return, which is the average of possible returns weighted by their likelihood of occurring. Familiarity with the science of statistics should aid in understanding the notion of expected outcome.
Given security A with 12 chances out of 100 of showing a return of −22%, 74 chances out of 100 of showing a return of 6% and 14 chances out of 100 of showing a return of 16%, its expected return would then be:
More generally, expected return or expected outcome is equal to:
where rt is a possible return and pt the probability of it occurring.
2/ STANDARD DEVIATION, A RISK-ANALYSIS TOOL
Intuitively, the greater the risk on an investment, the wider the variations in its return, and the more uncertain that return is. While the holder of a government bond is sure to receive their coupons (unless the government goes bankrupt!), this is far from true for the shareholder of a biotech company. They could lose everything, show a decent return or hit the jackpot.
Therefore, the risk carried by a security can be looked at in terms of the dispersion of its possible returns around an average return. Consequently, risk can be measured mathematically by the variance of its return, i.e. by the sum of the squares of the deviation of each return from expected outcome, weighted by the likelihood of each of the possible returns occurring, or:
Standard deviation in returns is the most often used measure to evaluate the risk of an investment. Standard deviation is expressed as the square root of the variance:
The variance of investment A above is therefore:
where V(r) = 1%, which corresponds to a standard deviation of 10%.
Section 18.4 MARKET AND SPECIFIC RISK
Risk in finance is materialised by fluctuation of value, which is equivalent to fluctuation of returns. Hence, one figure summarises all of the different risks, the knowledge of which does not really matter. Only the impact on value is important.
Fluctuations in the value of a security can be due to:
- fluctuations in the entire market. The market could rise as a whole after an unexpected cut in interest rates, stronger-than-expected economic growth figures, etc. All stocks will then rise, although some will move more than others. The same thing can occur when the entire market moves downward; or
- factors specific to the company that do not affect the market as a whole, such as a major order, the bankruptcy of a competitor, a new regulation affecting the company’s products, a scandal over fraud on product tests, discovering contaminated products, etc.
These two sources of fluctuation produce two types of risk: market risk and specific risk.
- Market, systematic or undiversifiable risk is due to trends in the entire economy, tax policy, interest rates, inflation, etc. Remember, this is the risk of the security correlated to market risk. To varying degrees, market risk affects all securities. For example, if a nation switches to a 35-hour working week with no adjustment in wages, all companies will be affected. However, in such a case, it stands to reason that textile makers will be affected more than cement companies.
- Specific, intrinsic or idiosyncratic risk is independent of market-wide phenomena and is due to factors affecting just the one company, such as mismanagement, a factory fire, an invention that renders a company’s main product line obsolete, etc. (In the next chapter, it will be shown how this risk can be eliminated by diversification, a reason why this risk is also sometimes call diversifiable risk.)
Market volatility can be economic or financial in origin, but it can also result from anticipation of flows (dividends, capital gains, etc.) or a variation in the cost of equity. For example, an overheating of the economy could raise the cost of equity (i.e. after an increase in the central bank rate) and reduce anticipated cash flows due to weaker demand. Together, these two factors could exert a double downward pressure on financial securities.
Since market risk and specific risk are independent, they can be measured independently and we can apply Pythagoras’s theorem (in more mathematical terms, the two risk vectors are orthogonal) to the overall risk of a single security:
The systematic risk presented by a financial security is frequently expressed in terms of its sensitivity to market fluctuations. This is done via a linear regression between periodic market returns (rMt) and the periodic returns of each security J: rJt. This yields the regression line expressed in the following equation:
βJ is a parameter specific to each investment J and it expresses the relationship between fluctuations in the value of J and the market. It is thus a coefficient of volatility or of sensitivity. We call it the beta or the beta coefficient.
A security’s total risk is reflected in the standard deviation of its return, s(rJ).
A security’s market risk is therefore equal to βJ × σ(rM), where σ(rM) is the standard deviation of the market return. Therefore it is also proportional to the beta, i.e. the security’s market-linked volatility. The higher the beta, the greater the market risk borne by the security. If β >1, then the security’s returns move at a ratio of greater than 1:1 with respect to the market. Conversely, securities whose beta is below 1 are less affected by market fluctuations.
The specific risk of security J is equal to the standard deviation of the different residuals εJ of the regression line, expressed as σ(εJ), i.e. the variations in the stock that are not tied to market variations.
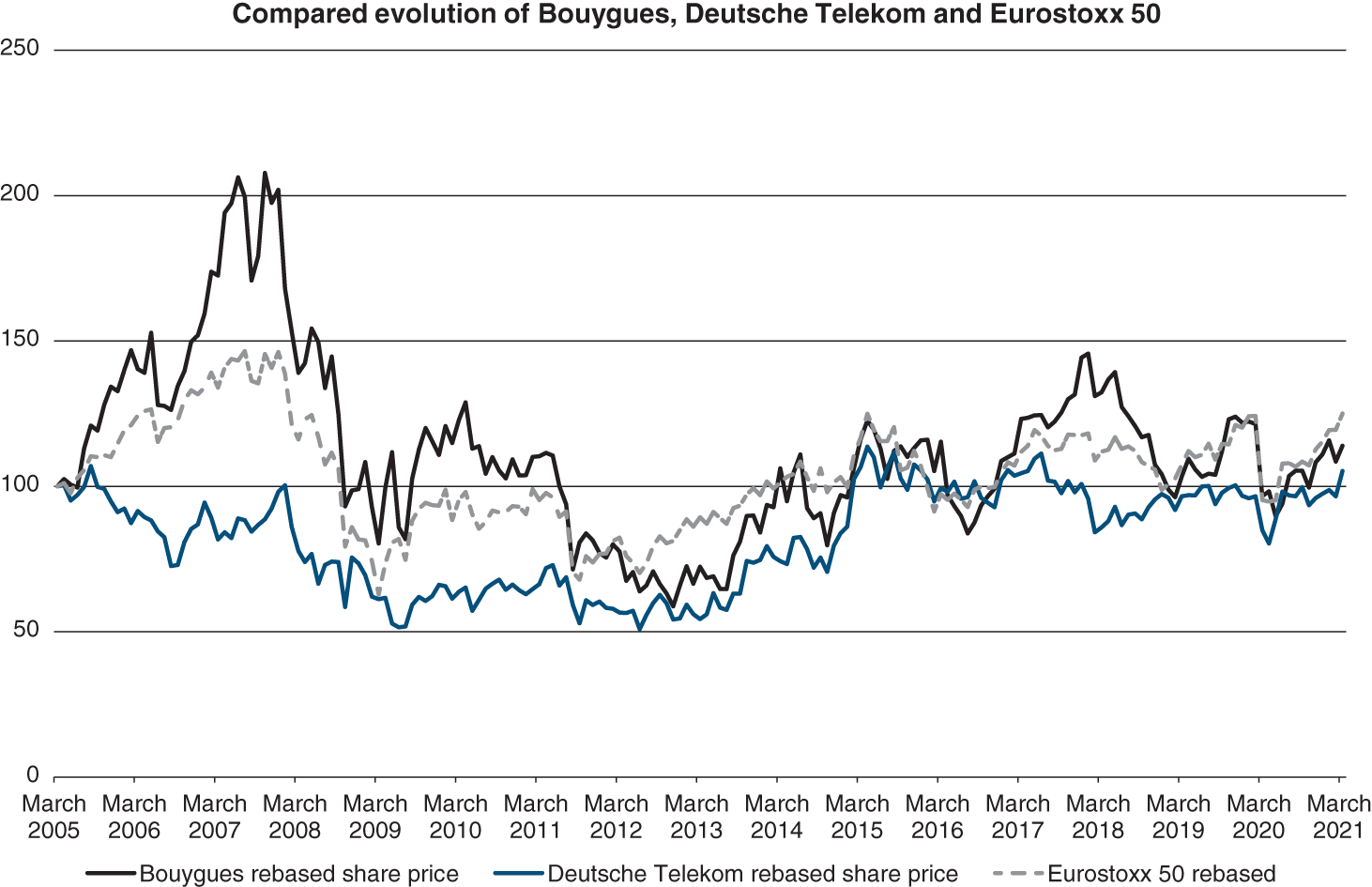
This chart shows that the β of Bouygues is higher than that of Deutsche Telekom.
Source: Data from Factset
This can be expressed mathematically as follows:
Section 18.5 THE BETA COEFFICIENT
1/ CALCULATING BETA
β measures a security’s sensitivity to market risk. For security J, it is mathematically obtained by performing a regression analysis of security returns versus market returns.
Hence:
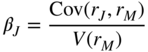
Here, Cov(rJ, rM) is the covariance of the return of security J with that of the market, and V(rM) is the variance of the market return. This can be represented as:
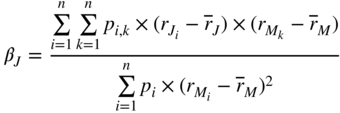
More intuitively, β corresponds to the slope of the regression of the security’s return versus that of the market. The line we obtain is defined as the characteristic line of a security.
As an example, we have calculated the β for Orange and it stands at 0.61.
The β of Orange used to be higher in the late 1990s (1.83). The stock was more volatile than the market, its market risk was high. With the mobile telecom and Internet market maturing, the industry became less risky and the β of Orange is now 1, as shown in the following graph:
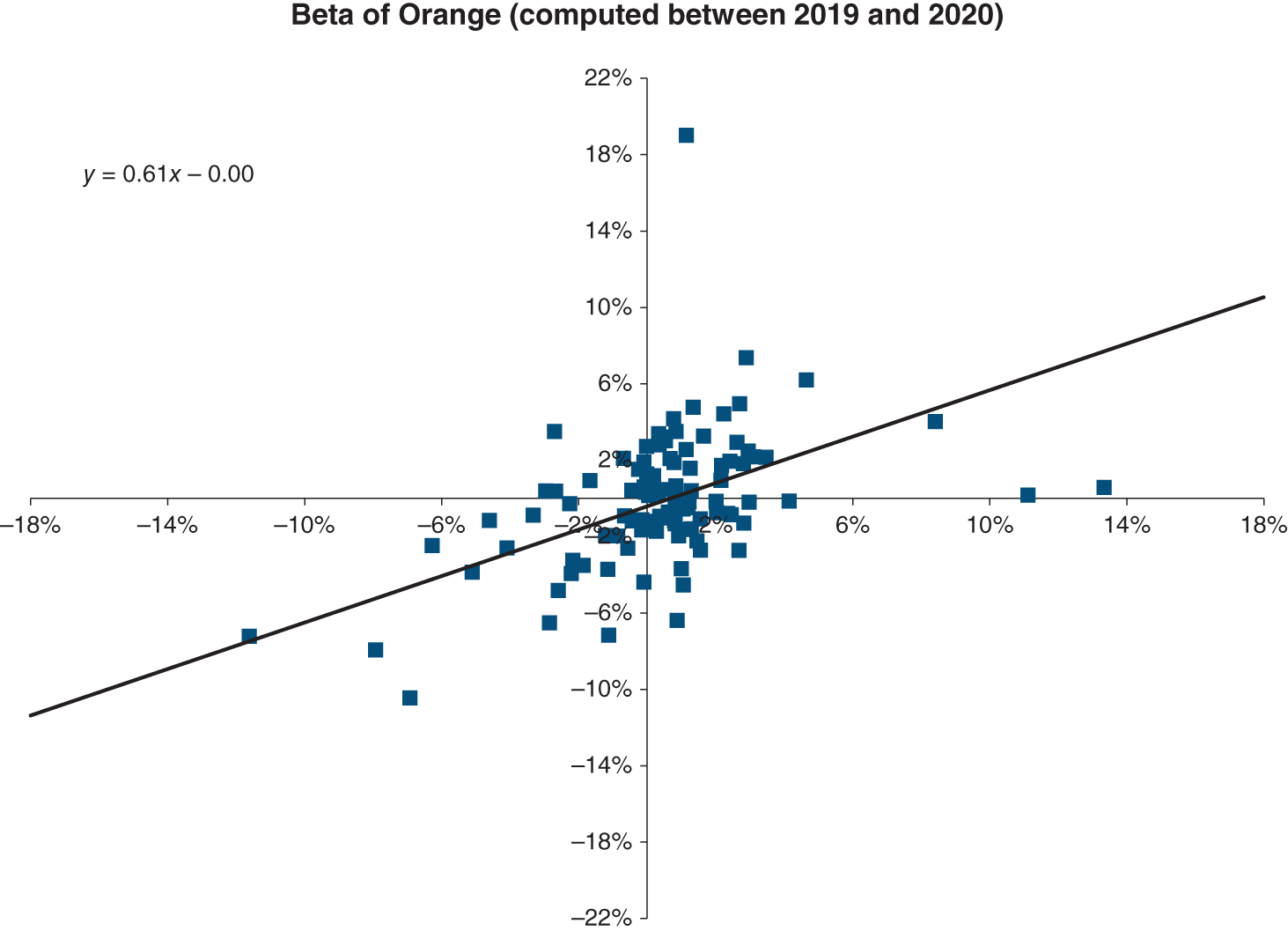
Source: Data from Factset
2/ PARAMETERS BEHIND BETA
By definition, the market β is equal to 1. β of fixed-income securities ranges from about 0 to 0.5. The β of equities is usually higher than 0.5, and normally between 0.5 and 1.5. We are not aware of any simple investment products with a negative β, and shares with a β greater than 2 are quite exceptional.
To illustrate, the table below presents betas, as of 2019, of the members of the Euro Stoxx 50 index:
| Beta of the Eurostoxx 50 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Linde | 0.47 | L’Oréal | 0.76 | SAP | 0.92 | Siemens | 1.07 | AXA | 1.21 |
| Royal Ahold Delhaize | 0.59 | Inditex | 0.76 | AB InBev | 0.92 | Bayer | 1.10 | ASML | 1.27 |
| Amadeus | 0.61 | Unilever | 0.77 | Vivendi | 0.92 | Telefonica | 1.12 | Volkswagen | 1.35 |
| Danone | 0.68 | Eni | 0.79 | Deutsche Post | 0.97 | Philips | 1.12 | ING | 1.38 |
| Deutsche Telekom | 0.68 | Adidas | 0.81 | Total | 0.97 | Daimler | 1.15 | BNP Paribas | 1.39 |
| EssilorLuxottica | 0.69 | Unibail-Rodamco-Westfield | 0.82 | Fresenius | 1.01 | Airbus | 1.16 | Nokia | 1.40 |
| Orange | 0.72 | Munich Re | 0.82 | Safran | 1.03 | LVMH | 1.17 | BBVA | 1.42 |
| Sanofi | 0.72 | Vinci | 0.87 | Allianz | 1.03 | Kering | 1.18 | Société Générale | 1.46 |
| Iberdrola | 0.75 | Engie | 0.88 | BMW | 1.06 | Schneider | 1.21 | Intesa Sanpaolo | 1.46 |
| Enel | 0.75 | Air Liquide | 0.91 | BASF | 1.07 | CRH | 1.21 | Santander | 1.56 |
Source: Factset, 2019
For a given security, the following parameters explain the value of beta:
(a) Sensitivity of the stock’s sector to the state of the economy
The greater the effect of the state of the economy on a business sector, the higher its β is – temporary work is one such highly exposed sector. Another example is automakers, which tend to have a β close to 1. There is an old saying in North America, “As General Motors goes, so goes the economy”. This serves to highlight how GM’s financial health is to some extent a reflection of the health of the entire economy. Thus, beta analysis can show how GM will be directly affected by macroeconomic shifts.
(b) Cost structure
The greater the proportion of fixed costs to total costs, the higher the breakeven point, and the more volatile the cash flows. Companies that have a high ratio of fixed costs (such as cement makers) have a high β, while those with a low ratio of fixed costs (such as mass-market service retailers) have a low β.
(c) Financial structure
The greater a company’s debt, the greater its financing costs. Financing costs are fixed costs which increase a company’s breakeven point and, hence, its earnings volatility. The heavier a company’s debt or the more heavily leveraged the company is, the higher the β of its shares is.
(d) Visibility on company performance
The quality of management and the clarity and quantity of information the market has about a company will all have a direct influence on its beta. All other factors being equal, if a company gives out little or low-quality information, the β of its stock will be higher as the market will factor the lack of visibility into the share price.
(e) Earnings growth
The higher the forecast rate of earnings growth, the higher the β. Most of a company’s value in cash flows is far down the road and thus highly sensitive to any change in assumptions.
Section 18.6 PORTFOLIO RISK
1/ THE FORMULA APPROACH
Consider the following two stocks, Heineken and Criteo, which have the following characteristics:
| Heineken % | Criteo % | |
|---|---|---|
| Expected return: E(r) | 6 | 13 |
| Risk: σ(r) | 10 | 17 |
As is clear from this table, Criteo offers a higher expected return while presenting a greater risk than Heineken. Inversely, Heineken offers a lower expected return but also presents less risk.
These two investments are not directly comparable. Investing in Criteo means accepting more risk in exchange for a higher return, whereas investing in Heineken means playing it relatively safe.
Therefore, there is no clear-cut basis by which to choose between Criteo and Heineken. However, the problem can be looked at in another way: would buying a combination of Criteo and Heineken shares be preferable to buying just one or the other?
It is likely that the investor will seek to diversify and create a portfolio made up of Criteo shares (in a proportion of XC) and Heineken shares (in a proportion of XH). This way, they will expect a return equal to the weighted average return of each of these two stocks, or:
where XC + XH = 1.
Depending on the proportion of Criteo shares in the portfolio (XC), the portfolio would look like this:
| XC (%) | 0 | 25 | 33.3 | 50 | 66.7 | 75 | 100 |
| E(rH,C) (%) | 6 | 7.8 | 8.3 | 9.5 | 10.7 | 11.3 | 13 |
The portfolio’s variance is determined as follows:
where Cov(rH, rC) is the covariance. It measures the degree to which Heineken and Criteo fluctuate together. It is equal to:
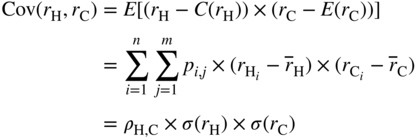
Here, pi,j is the probability of joint occurrence and ρH,C is the correlation coefficient of returns offered by Heineken and Criteo. The correlation coefficient is a number between −1 (where the correlation between returns on the two stocks will be perfectly negative) and 1 (where the correlation between returns on the two stocks will be perfectly positive). Correlation coefficients are usually positive, as most stocks rise together in a bullish market and fall together in a bearish market.
By plugging the variables back into our variance equation above, we obtain:
Given that:
it is therefore possible to say:
or:
Therefore, the overall risk of a portfolio consisting of Criteo and Heineken shares is less than the weighted average of the risks of the two stocks.
Assuming that ρH,C is equal to 0.5 (from the figures in the above example), we obtain the following:
| X (%) | 0 | 25 | 33.3 | 50 | 66.7 | 75 | 100 |
| σ(rH,C) (%) | 10.0 | 10.3 | 10.7 | 11.8 | 13.3 | 14.2 | 17.0 |
Hence, a portfolio consisting of 50% Criteo and 50% Heineken has a standard deviation of 11.8% or less than the average of Criteo and Heineken, which is (50% × 17%) + (50% × 10%) = 13.5%.
On a chart, it looks like this:
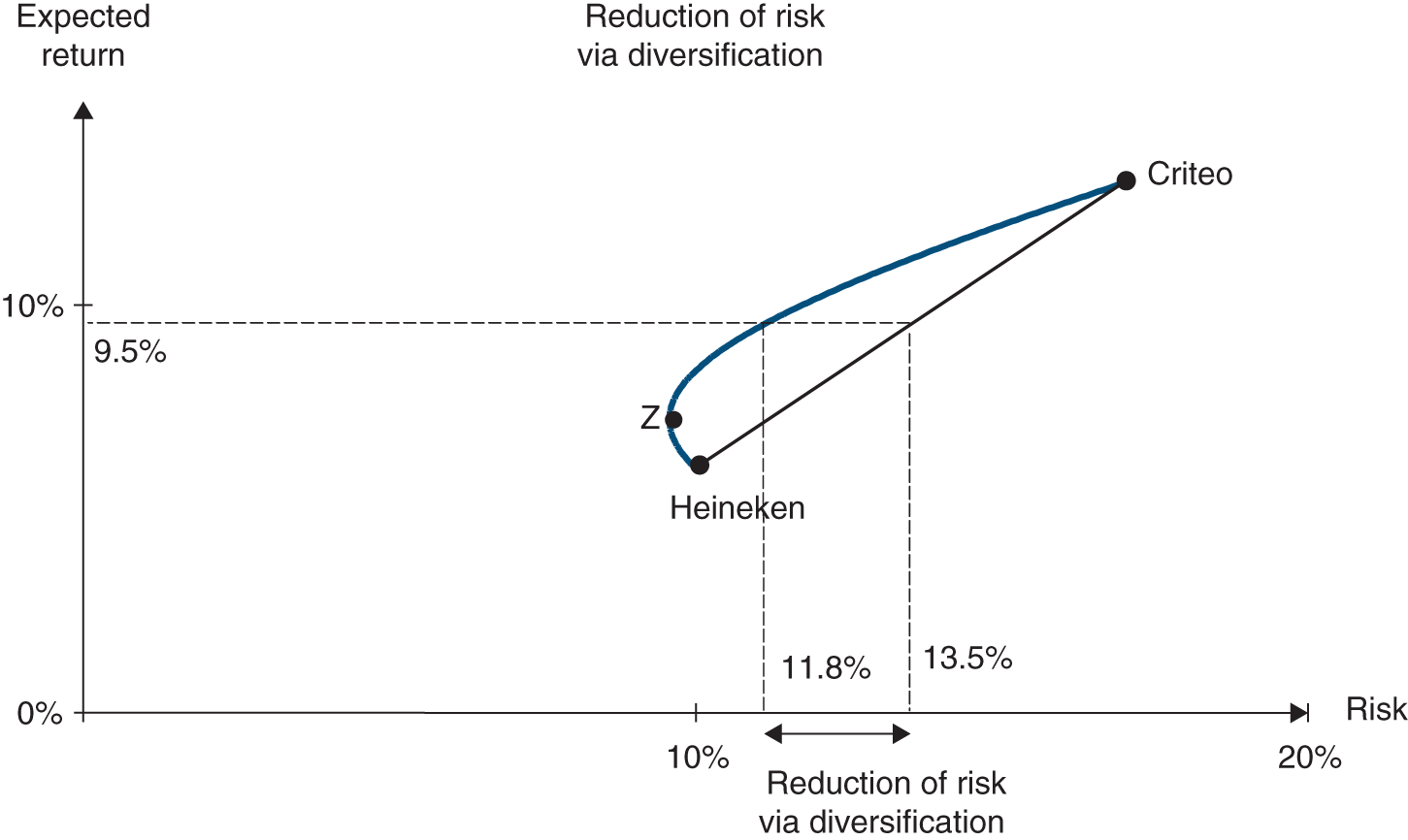
Only a correlation coefficient of 1 creates a portfolio risk that is equal to the average of its component risks.
CORRELATION BETWEEN DIFFERENT STOCK MARKETS (2014–2019)
| Brazil | China | France | Germany | Morocco | Switzerland | UK | United States | |
|---|---|---|---|---|---|---|---|---|
| Brazil | 1.00 | 0.30 | 0.68 | 0.67 | 0.82 | 0.38 | 0.72 | 0.90 |
| China | 0.30 | 1.00 | 0.66 | 0.70 | 0.44 | 0.52 | 0.36 | 0.47 |
| France | 0.68 | 0.66 | 1.00 | 0.97 | 0.78 | 0.69 | 0.82 | 0.84 |
| Germany | 0.67 | 0.70 | 0.97 | 1.00 | 0.84 | 0.63 | 0.84 | 0.83 |
| Morocco | 0.82 | 0.44 | 0.78 | 0.84 | 1.00 | 0.40 | 0.83 | 0.85 |
| Switzerland | 0.38 | 0.52 | 0.69 | 0.63 | 0.40 | 1.00 | 0.54 | 0.46 |
| UK | 0.72 | 0.36 | 0.82 | 0.84 | 0.83 | 0.54 | 1.00 | 0.77 |
| United States | 0.90 | 0.47 | 0.84 | 0.83 | 0.85 | 0.46 | 0.77 | 1.00 |
Source: Data from Factset
Emerging markets still bring diversification and are more correlated among themselves than with developed countries.
However, sector diversification is still highly efficient thanks to the low correlation coefficients among different industries:
CORRELATION BETWEEN ECONOMIC SECTORS WORLDWIDE (2014–2019)
| Sector | Banks | Automotive | Pharmaceuticals & Biotech | Oil & Gas | Construction | Softwares | Energy | Agriculture & Food chain | Retailing | Metals & Mining | Aerospace & Defence |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Banks | 1.00 | 0.75 | 0.52 | 0.35 | 0.66 | 0.74 | 0.26 | 0.56 | 0.66 | 0.71 | 0.79 |
| Automotive | 0.75 | 1.00 | 0.49 | 0.24 | 0.43 | 0.28 | 0.21 | 0.31 | 0.24 | 0.38 | 0.35 |
| Pharmaceuticals & Biotech | 0.52 | 0.49 | 1.00 | −0.20 | 0.54 | 0.57 | −0.30 | 0.73 | 0.64 | 0.00 | 0.56 |
| Oil & Gas | 0.35 | 0.24 | −0.20 | 1.00 | −0.25 | 0.04 | 0.99 | −0.25 | −0.03 | 0.79 | 0.11 |
| Construction | 0.66 | 0.43 | 0.54 | −0.25 | 1.00 | 0.77 | −0.34 | 0,89 | 0,74 | 0,24 | 0.76 |
| Softwares | 0.74 | 0.28 | 0.57 | 0.04 | 0.77 | 1.00 | −0.10 | 0.78 | 0.97 | 0.48 | 0.99 |
| Energy | 0.26 | 0.21 | −0.30 | 0.99 | −0.34 | −0.10 | 1.00 | −0.36 | −0.16 | 0.72 | −0.02 |
| Agriculture & Food chain | 0.56 | 0.31 | 0.73 | −0.25 | 0.89 | 0.78 | −0.36 | 1.00 | 0.78 | 0.15 | 0.76 |
| Retailing | 0.66 | 0.24 | 0.64 | −0.03 | 0.74 | 0.97 | −0.16 | 0.78 | 1.00 | 0.36 | 0.95 |
| Metals & Mining | 0.71 | 0.38 | 0.00 | 0.79 | 0.24 | 0.48 | 0.72 | 0.15 | 0.36 | 1.00 | 0.55 |
| Aerospace & Defence | 0.79 | 0.35 | 0.56 | 0.11 | 0.76 | 0.99 | −0.02 | 0.76 | 0.95 | 0.55 | 1.00 |
Source: Data from Factset
Section 18.7 CHOOSING AMONG SEVERAL RISKY ASSETS AND THE EFFICIENT FRONTIER
This section will address the following questions: why is it correct to say that the beta of an asset should be measured in relation to the market portfolio? Above all, what is the market portfolio?
To begin, it is useful to study the impact of the correlation coefficient on diversification. Again, the same two securities will be analysed: Criteo (C) and Heineken (H). By varying ρH,C between −1 and +1, we obtain:
| Proportion of C shares in portfolio (XC) (%) | 0 | 25 | 33.3 | 50 | 66.7 | 75 | 100 | |
|---|---|---|---|---|---|---|---|---|
| Return on the portfolio: E(rH,C) (%) | 6.0 | 7.8 | 8.3 | 9.5 | 10.7 | 11.3 | 13.0 | |
| Portfolio risk σ(rH,C) (%) | ρH,C = −1 | 10.0 | 3.3 | 1.0 | 3.5 | 8.0 | 10.3 | 17.0 |
| ρH,C = −0.5 | 10.0 | 6.5 | 6.2 | 7.4 | 10.1 | 11.7 | 17.0 | |
| ρH,C = 0 | 10.0 | 8.6 | 8.7 | 9.9 | 11.8 | 13.0 | 17.0 | |
| ρH,C = 0.3 | 10.0 | 9.7 | 10.0 | 11.1 | 12.7 | 13.7 | 17.0 | |
| ρH,C = 0.5 | 10.0 | 10.3 | 10.7 | 11.8 | 13.3 | 14.2 | 17.0 | |
| ρH,C = 1 | 10.0 | 11.8 | 12.3 | 13.5 | 14.7 | 15.3 | 17.0 |
Note the following caveats:
- If Criteo and Heineken were perfectly correlated (i.e. the correlation coefficient was 1), then diversification would have no effect. All possible portfolios would lie on a line linking the risk/return point of Criteo with that of Heineken. Risk would increase in direct proportion to Criteo’s stock added.
- If the two stocks were perfectly inversely correlated (correlation coefficient −1), then diversification would be total. However, there is little chance of this occurring, as both companies are exposed to the same economic conditions.
- Generally speaking, Criteo and Heineken are positively, but imperfectly, correlated and diversification is based on the desired amount of risk.
With a fixed correlation coefficient of 0.3, there are portfolios that offer different returns at the same level of risk. Thus, a portfolio consisting of two-thirds Heineken and one-third Criteo shows the same risk (10%) as a portfolio consisting of just Heineken, but returns 8.3% versus only 6% for Heineken.
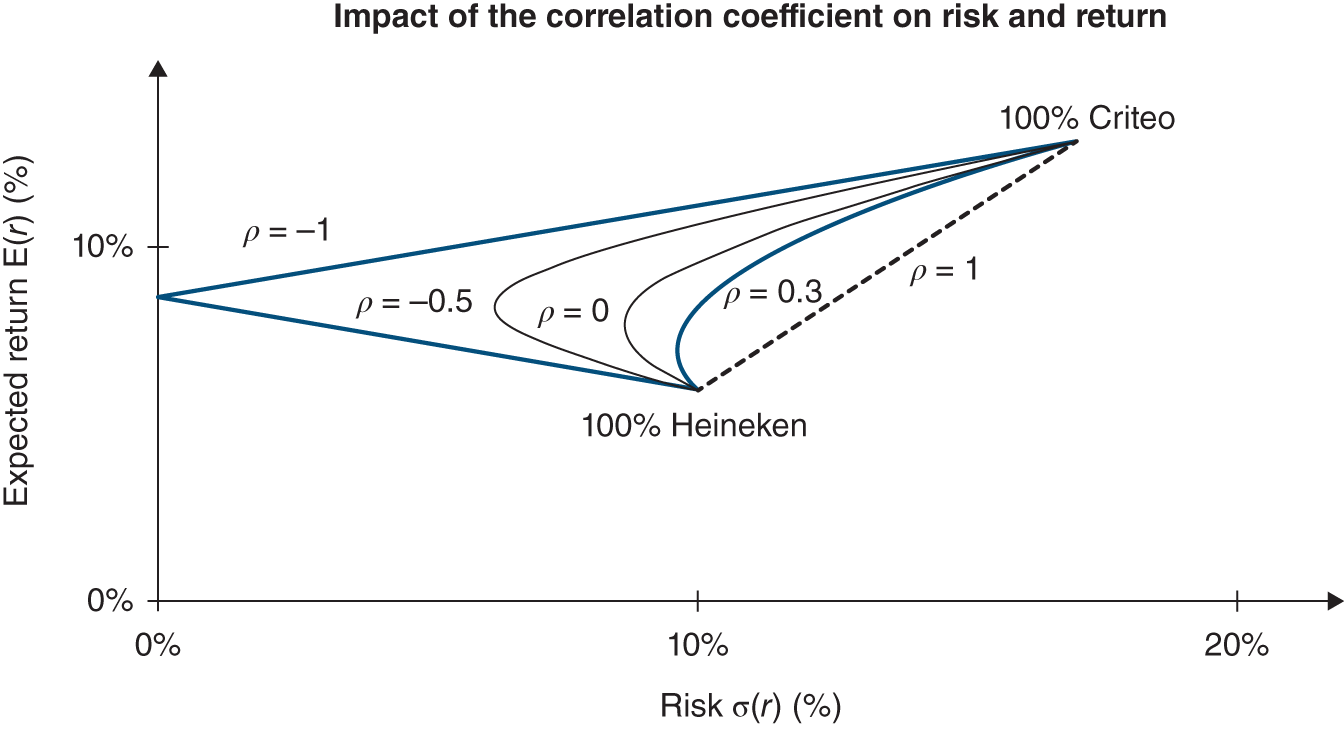
There is no reason for an investor to choose a given combination if another offers a better (efficient) return at the same level of risk.
Efficient portfolios (such as a combination of Criteo and Heineken shares) offer investors the best risk–return ratio (i.e. minimum risk for a given return).
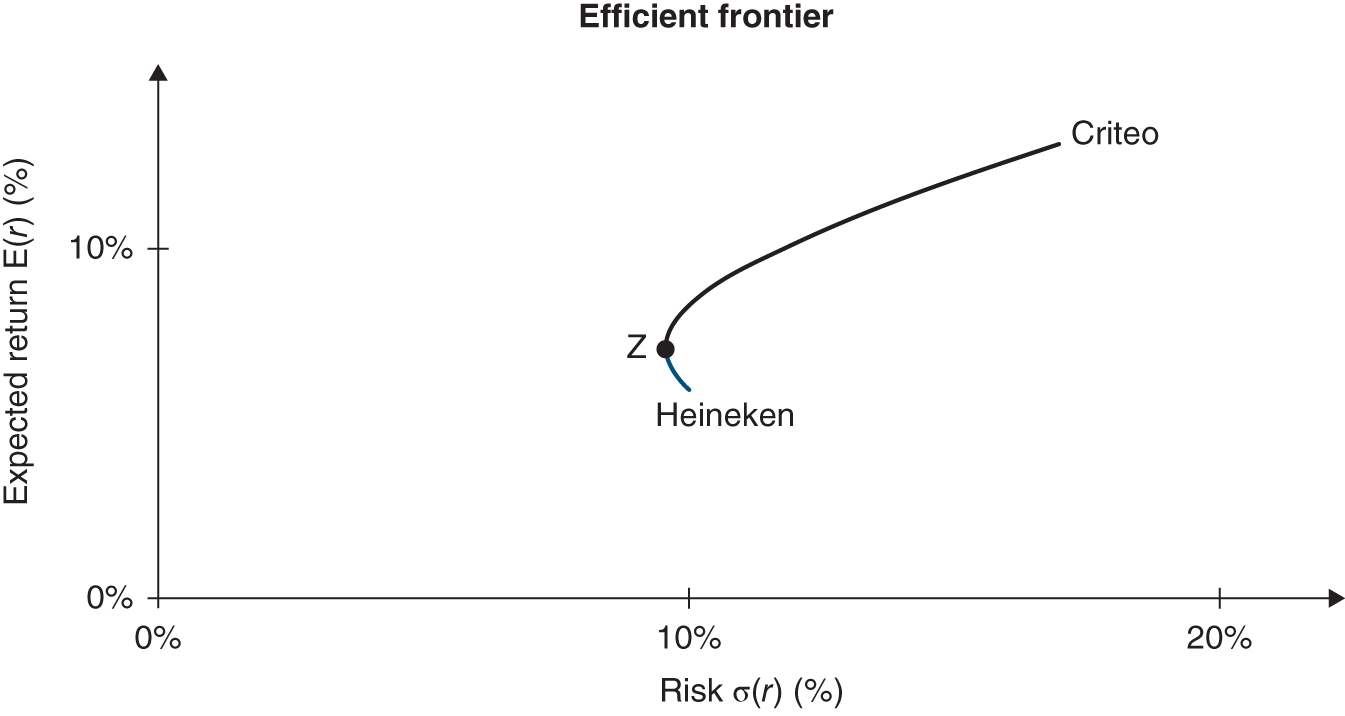
For any portfolio that does not lie on the efficient frontier, another can be found that, given the level of risk, offers a greater return or that, at the same return, entails less risk.
With a larger number of stocks, i.e. more than just two, the investor can improve their efficient frontier, as shown in the following chart.
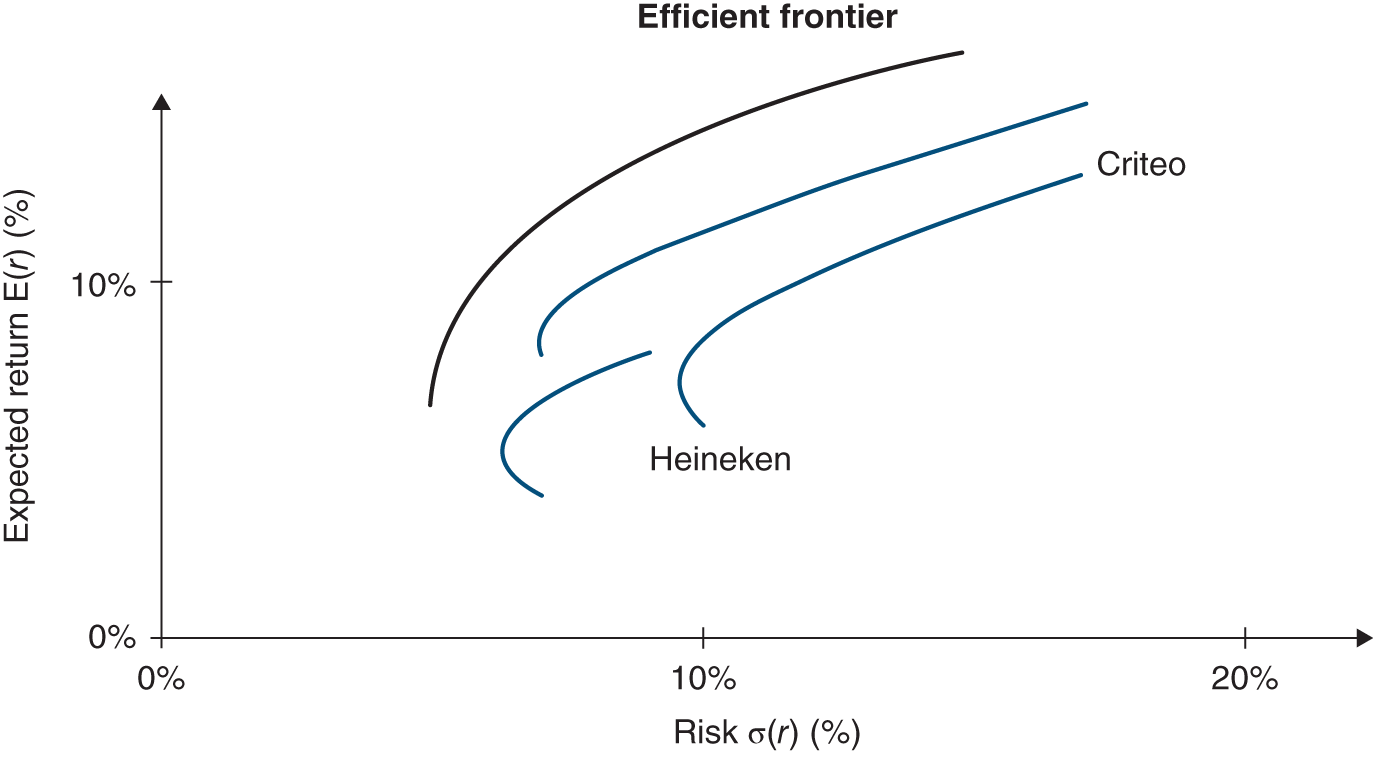
Section 18.8 CHOOSING BETWEEN SEVERAL RISKY ASSETS AND A RISK-FREE ASSET: THE CAPITAL MARKET LINE
1/ RISK-FREE ASSETS
By definition, risk-free assets are those whose returns, the risk-free rate (rF), are certain. The standard deviation of their return is thus zero. Traditionally, this is illustrated with government bonds, although we can no longer assume that the government cannot go bankrupt, given the high levels of debt in many countries. This has now led us to view the 1-month Treasury bill as risk-free (e.g. the German bill for the Eurozone, the US Treasury bill for the US).
If a portfolio has a risk-free asset F in proportion (1 − XH) and the portfolio consists exclusively of Heineken shares, then the portfolio’s expected return E(rH,F) will be equal to:
The portfolio’s expected return is equal to the return of the risk-free asset, plus a risk premium, multiplied by the proportion of Heineken shares in the portfolio. The risk premium is the difference between the expected return on Heineken and the return on the risk-free asset.
How much risk does the portfolio carry? Its risk will simply be the risk of the Heineken stock, commensurate with its proportion in the portfolio, expressed as follows:
If investors want to increase their expected return, they will increase XH. They could even borrow money at the risk-free rate and use the funds to buy Heineken stock, but the risk carried by their portfolio would rise commensurately.
By combining the previous two equations, we can eliminate XH, thus deriving the following equation:
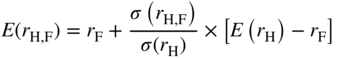
Continuing with the Heineken example, and assuming that rF is 3%, with 50% of the portfolio consisting of a risk-free asset, the following is obtained:
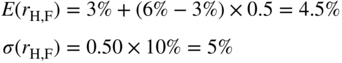
Hence:
For a portfolio that includes a risk-free asset, there is a linear relationship between expected return and risk. To lower a portfolio’s risk, simply liquidate some of the portfolio’s stock and put the proceeds into a risk-free asset. To increase risk, it is only necessary to borrow at the risk-free rate and invest in a stock with risk.
2/ RISK-FREE ASSETS AND THE EFFICIENT FRONTIER
The risk–return profile can be chosen by combining risk-free assets and a stock portfolio (the alpha portfolio on the chart below). This new portfolio will be on a line that connects the risk-free rate to the portfolio alpha that has been chosen. But as we can observe on the chart, this portfolio is not the best portfolio. Portfolio P provides a better return for the same risk. Portfolio P is situated on the line tangential to the efficient frontier. There is no other portfolio than P that offers a better return for the same amount of risk-taking. What is portfolio P made up of? It’s made up of a combination of the portfolio of risky assets M (located on the efficient frontier at the tangential point with the line originating from the risk-free rate) and the risk-free asset.
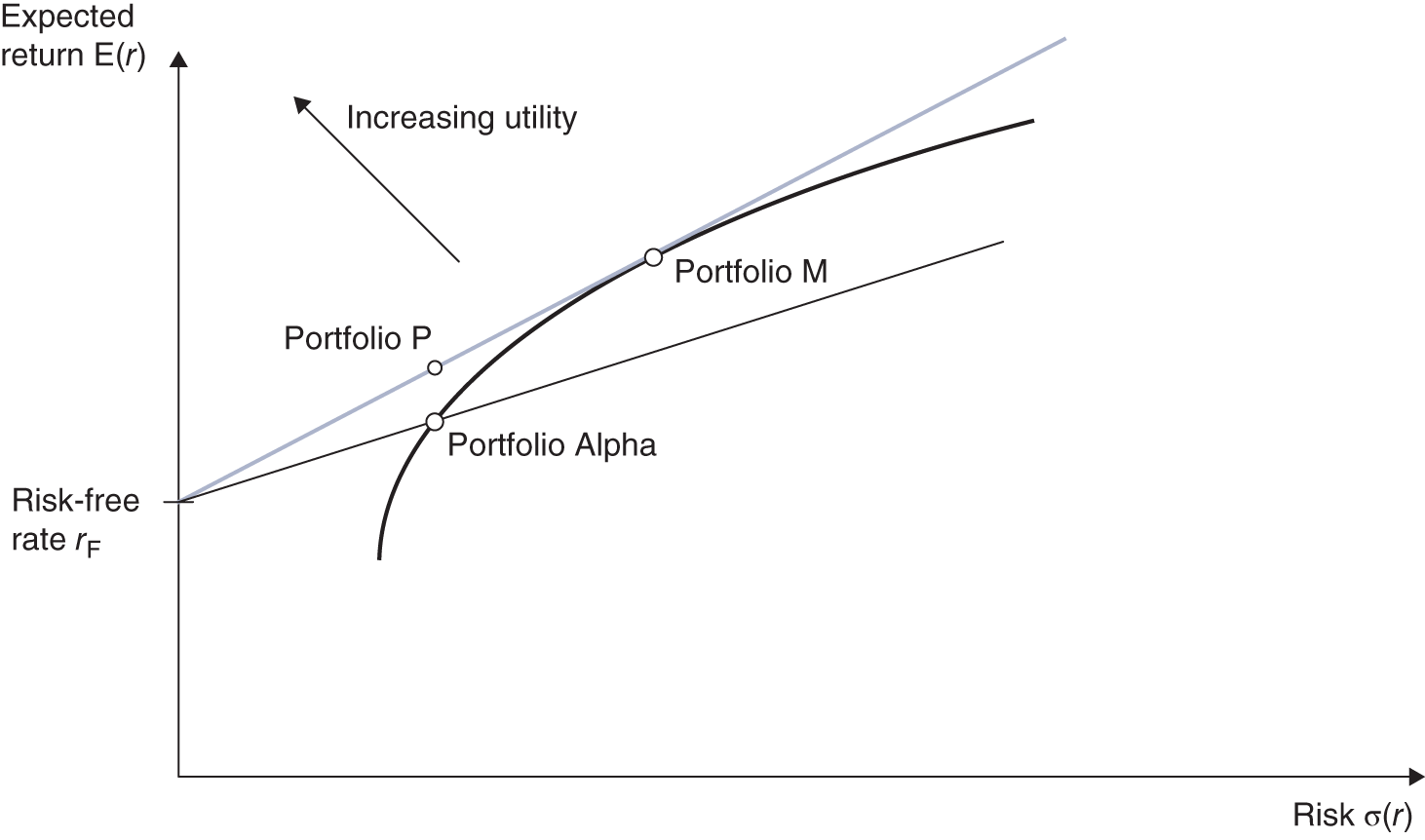
Investors’ taste for risk can vary, yet the above graph demonstrates that the shrewd investor should be investing in portfolio M. It is then a matter of adjusting the risk exposure by adding or subtracting risk-free assets.
If all investors acquire the same portfolio, then this portfolio must contain all existing shares. To understand why, suppose that stock i was not in portfolio M. In that case, nobody would want to buy it, since all investors hold portfolio M. Consequently, there would be no market for it and it would cease to exist.
The weighting of stock i in a market portfolio will necessarily be the value of the single security divided by the sum of all the assets. As we are assuming fair value, this will be the fair value of i.
3/ CAPITAL MARKET LINE
The expected return of a portfolio consisting of the market portfolio and the risk-free asset can be expressed by the following equation:
where E(rP) is the portfolio’s expected return, rF the risk-free rate, E(rM) the return on the market portfolio, σP the portfolio’s risk and σM the risk of the market portfolio.
This is the equation of the capital market line.
The most efficient portfolios in terms of return and risk will always be on the capital market line. The tangent point at M constitutes the optimal combination for all investors. If we introduce the assumption that all investors have homogeneous expectations, i.e. that they have the same opinions on expected returns and risk of financial assets, then the efficient frontier of risky assets will be the same for all of them. The capital market line is the same for all investors and thus each of them would hold a combination of the portfolio M and the risk-free asset.
It is reasonable to say that the portfolio M includes all the assets weighted for their market capitalisation. This is defined as the market portfolio. The market portfolio is the portfolio that all investors hold a fraction of, proportional to the market’s capitalisation.
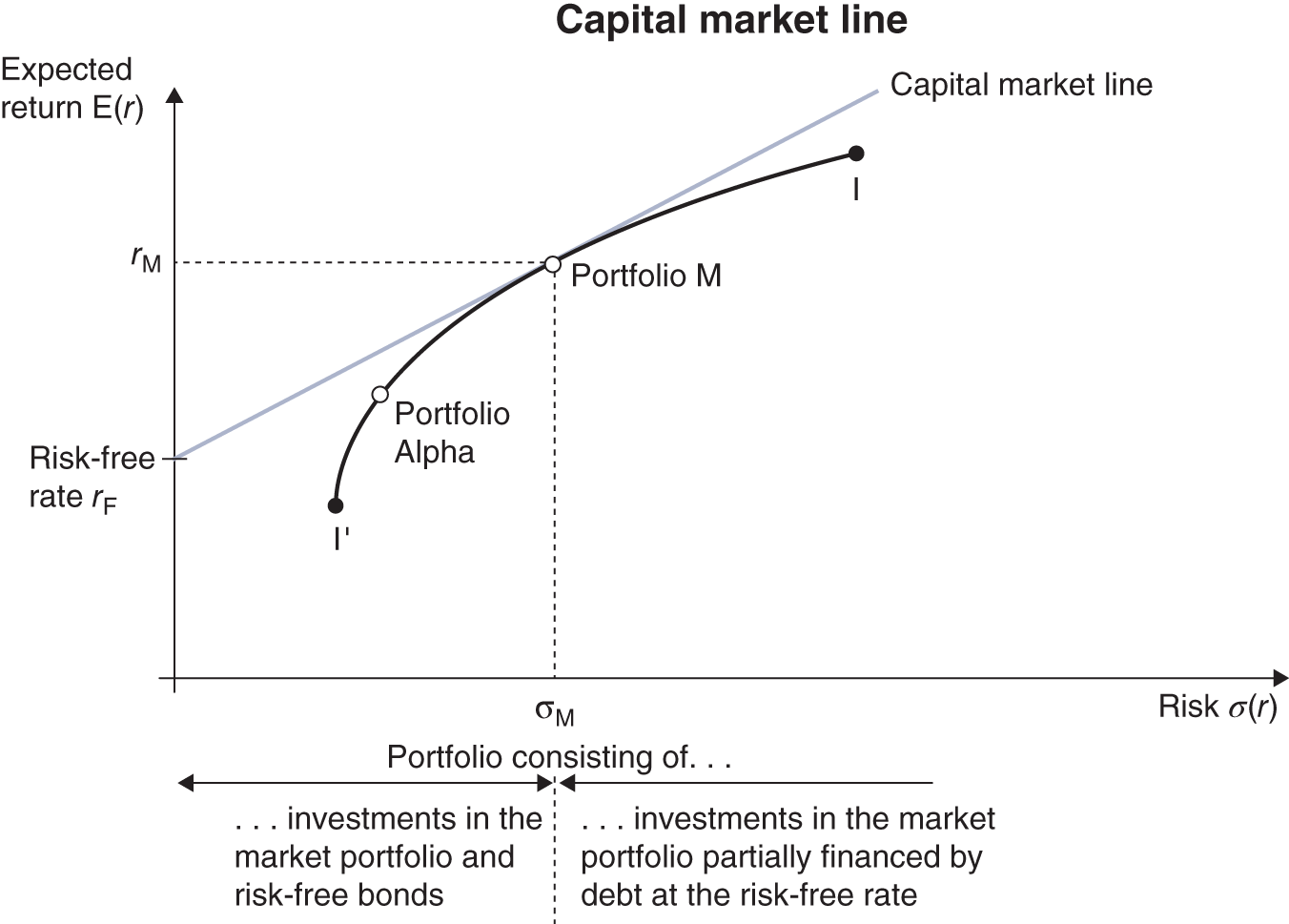
Section 18.9 HOW PORTFOLIO MANAGEMENT WORKS
The financial theory described so far seems to give a clear suggestion: in efficient markets, invest only in highly diversified mutual funds and in government bonds.
The asset management industry is one of the most important industries in the modern economy, managing €55,000bn worldwide (40% of this amount being invested in shares and 22% in bonds, the rest in short-term debts and multi-assets). Managers are employees of banks, insurance companies or independent.
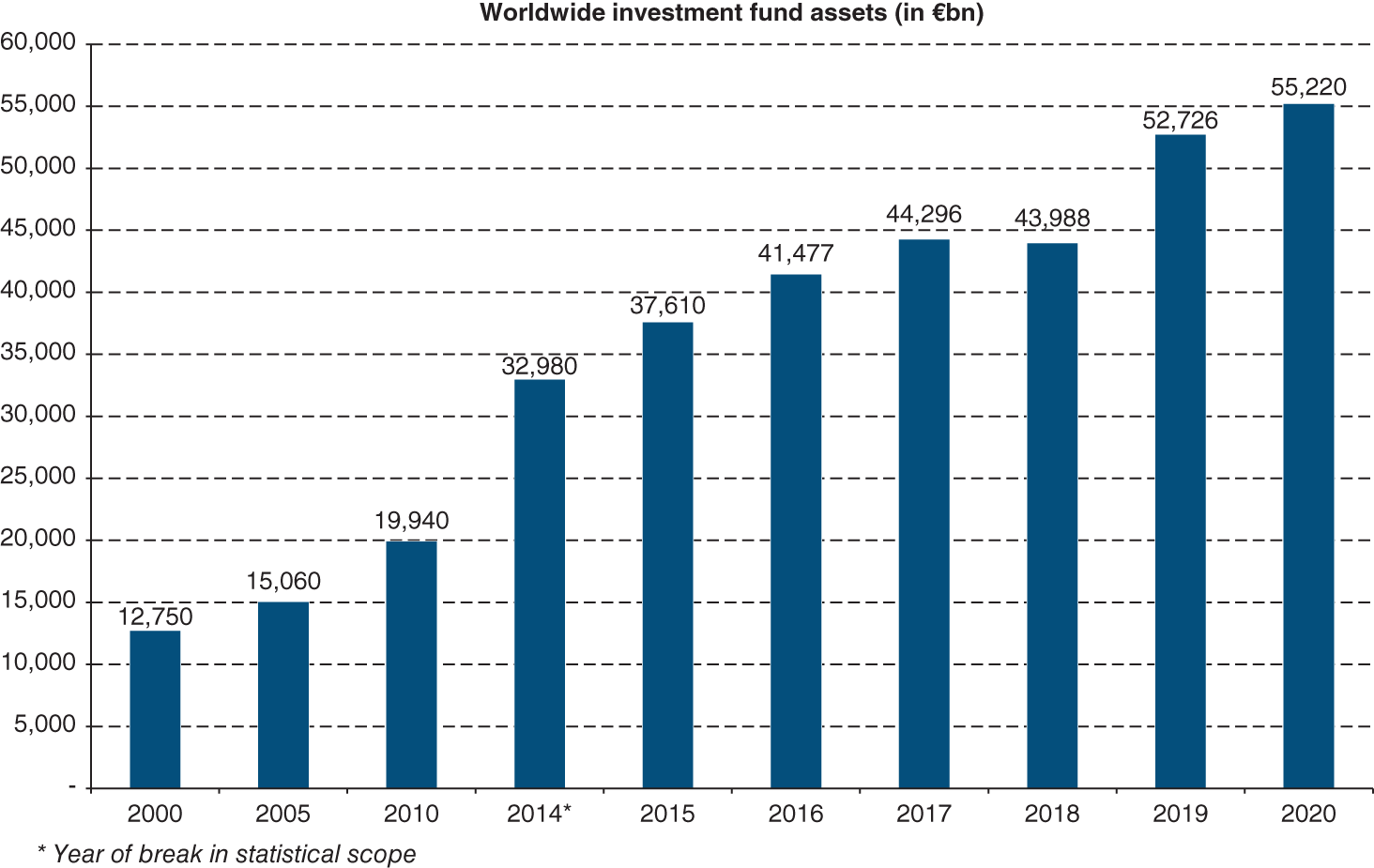
Source: Data from Efama
However, as our readers know, not all investors subscribe to this theory. Some take other approaches, described below. Sometimes investors combine different approaches.
The strategy that is closest to financial theory is index tracking, also known as passive management. It consists of trying to follow the performance of a market index. Index trackers are ideal tools for the investor who believes strongly in market efficiency. They also benefit from scale effect and therefore have reduced operating costs. Index trackers can be listed on a market and are then called exchange-traded funds (ETFs). Most stock markets now have a specific market segment for the listing of trackers. Across global markets, over 7,845 trackers are listed for a total amount of over $8,331bn.
In terms of portfolio management, we shall consider the difference between a top-down and a bottom-up approach. In a top-down approach, investors focus on the asset class (shares, bonds, money-market funds) and the international markets in which they wish to invest (i.e. the individual securities chosen are of little importance). In a bottom-up approach (commonly known as stock-picking), investors choose stocks on the basis of their specific characteristics, not the sector in which they belong. The goal of the bottom-up approach is to find that rare pearl, i.e. the stock that is undervalued by the market, which is identified through fundamental analysis, a method of seeking the intrinsic value of a stock. Investors following this approach believe that sooner or later, market value will approach intrinsic value.
These stocks can be growth stocks, i.e. companies who are operating in a fast-growing industry; or value stocks, i.e. firms operating in more mature sectors but which offer long-term performance. At the opposite end you will find yield stocks whose return comes almost exclusively from the dividend paid, and their market price is then pretty stable.
Investors who focus on technical analysis, the so-called chartists, do not seek to determine the value of a stock. Instead, these investors conduct detailed studies of trends in a stock’s market value and transaction volumes in the hope of spotting short-term trends.
Another type of fund management has arisen since the mid-1990s, so-called alternative management, which gives itself total freedom of investment tools, whether listed or not: equities, bonds, currencies, commodities, etc., and of investment styles: buying, short selling, derivatives (see Chapter 23), heavy reliance on debt, and shareholder activism. Its objective is not to duplicate the performance of any index, but to obtain positive returns regardless of the state of the market and thus to offer additional diversification. An example of alternative management is the hedge fund, which is a speculative fund seeking high returns and relying heavily on derivatives, and options in particular. Hedge funds use leverage and commit capital in excess of their equity.
At the beginning of 2021, over 7,000 hedge funds were active in the world and had about $3,800bn under management.
In recent years, hedge funds’ risk-adjusted performance has been above that of traditional management, this even in bearish markets, with a relatively low correlation with other investment opportunities.
Hedge funds may present some restrictions on investing (minimum size). Funds of funds allow a larger number of investors to invest in hedge funds. The funds of funds pick up the best hedge fund managers and package their products to be offered to a wide number of investors.
Last but not least are private equity funds, which invest mainly in non-listed firms at different stages of maturity, via LBOs or otherwise (see Chapter 47). Their growing scope of investments is slowly turning them into an alternative to stock markets.
Regardless of the investment strategies and tools used, asset management is currently witnessing a rise in responsible investment, which applies environmental, social and governance (ESG, see Chapter 1) criteria to investment choices. Worldwide, approximately a third of assets under management are managed according to ESG criteria. This figure reaches 49% in Europe. Under the influence of the ultimate beneficiaries of these funds, and the conviction of a certain number of managers, responsible investment is becoming the norm, especially since in some countries regulations require managers to explicitly detail their policies with regards to ESG criteria.
Within this category, SRI (socially responsible investment, see Chapter 1) strategies focus on selecting the most advanced companies in terms of sustainable development.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTE
Chapter 19. THE REQUIRED RATE OF RETURN
A ship in a harbour is safe but that is not what ships are built for
The previous chapter described the important concepts of risk, return and the market portfolio. It also highlighted the notion of risk premium (i.e. the difference between the return on the portfolio and the risk-free rate); this chapter continues to explore the risk premium in greater depth.
Investors must look at the big picture, first by investing in the market portfolio, then by borrowing or by investing in risk-free instruments commensurate with the level of risk they wish to assume. This approach allows them to assess an investment by merely determining the additional return and risk it adds to the market portfolio.
We now want to know how to get from r (the discounting rate used in calculating company value) to k (the return required by investors on a specific security).
Remember that this approach applies only if the investor owns a perfectly diversified portfolio.
Here is why: the greater the risk assumed by the financial investor, the higher their required rate of return. However, if they make just one investment and that turns out to be a failure, their required rate of return will matter little, as they will have lost everything.
With this in mind, it is easier to understand that the risk premium is relevant only if the financial investor manages not just a single investment, but a diversified portfolio of investments. In this case, the failure of one investment should be offset by the return achieved by other investments, which should thereby produce a suitable return for the portfolio as a whole.
This is the main difference between an industrial investment and a financial investment.
An entrepreneur who sets up their own company does not act like a financial investor, as they own just one investment. As their assets are not diversified, it is a matter of “life or death” for the firm that the investment succeeds. The law of averages in risk diversification does not apply to them.1
The financial investor, on the other hand, needs portfolio management tools to estimate the risk–return on each of their investments. Portfolio theory is not the main objective here, but it is useful to introduce some basic notions with which financial managers must be familiar.
Section 19.1 RETURN REQUIRED BY INVESTORS: THE CAPM
The CAPM (capital asset pricing model) was developed in the late 1950s and 1960s. Based on the work of Harry Markowitz, William Sharpe, John Lintner and Jack Treynor, it is now universally applied.
The CAPM is based on the assumption that investors act rationally and have at their disposal all relevant information on financial securities (see “efficient markets” in Chapter 15). Like the investor in Chapter 18, they seek to maximise their return, at a given level of risk.
The capital market line that we described in the previous chapter set the relationship for the return of a portfolio. CAPM aims at defining the same relationship but for a specific security (and not for a portfolio) in order to determine the return required for this security depending on its risk.
Remember that in order to minimise total risk, investors seek to reduce that component which can be reduced, i.e. the specific risk. They do so by diversifying their portfolios.
It can be observed that diversification reduces specific risk fairly quickly.
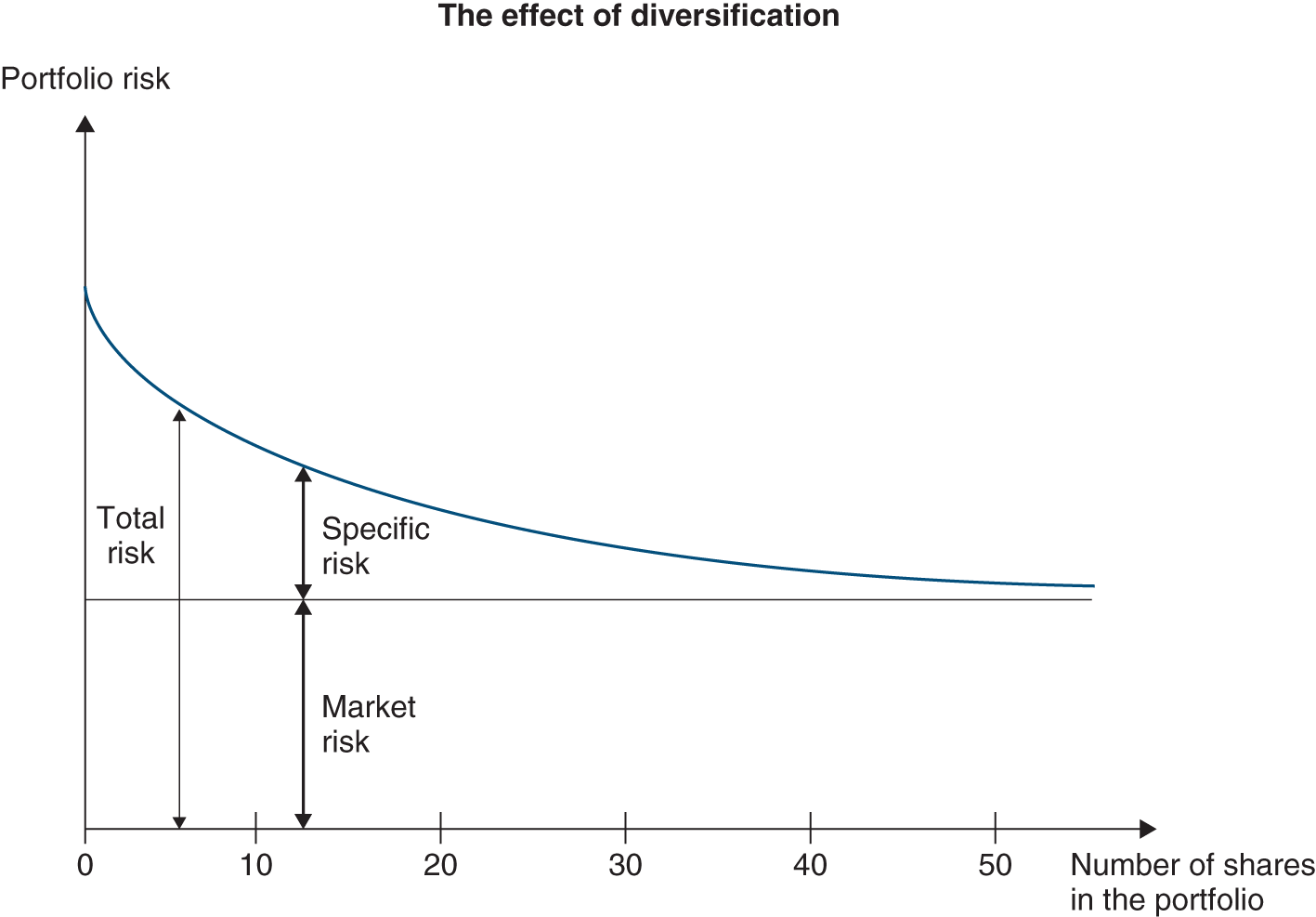
As a result, when stocks are fairly valued, investors will receive a return only on the portion of risk that they cannot eliminate – the market risk, or the non-diversifiable risk. Indeed, in a market in which arbitrage is theoretically possible, they will not be amply remunerated for a risk that they could otherwise eliminate themselves by simply diversifying their portfolios.
This means that the required rate of return (k) is equal to the risk-free rate rF,2 plus the risk premium for the non-diversifiable risk, i.e. the market risk.
This can be expressed as follows:
where kM is the required rate of return for the market and β the sensitivity coefficient described previously.
Note that the coefficient β measures the non-diversifiable risk of an asset and not its total risk. So it is possible to have a stock that is, on the whole, highly risky but with a low β if it is only loosely correlated with the market.
The difference between the return expected on the market as a whole and the risk-free rate is called the equity risk premium.
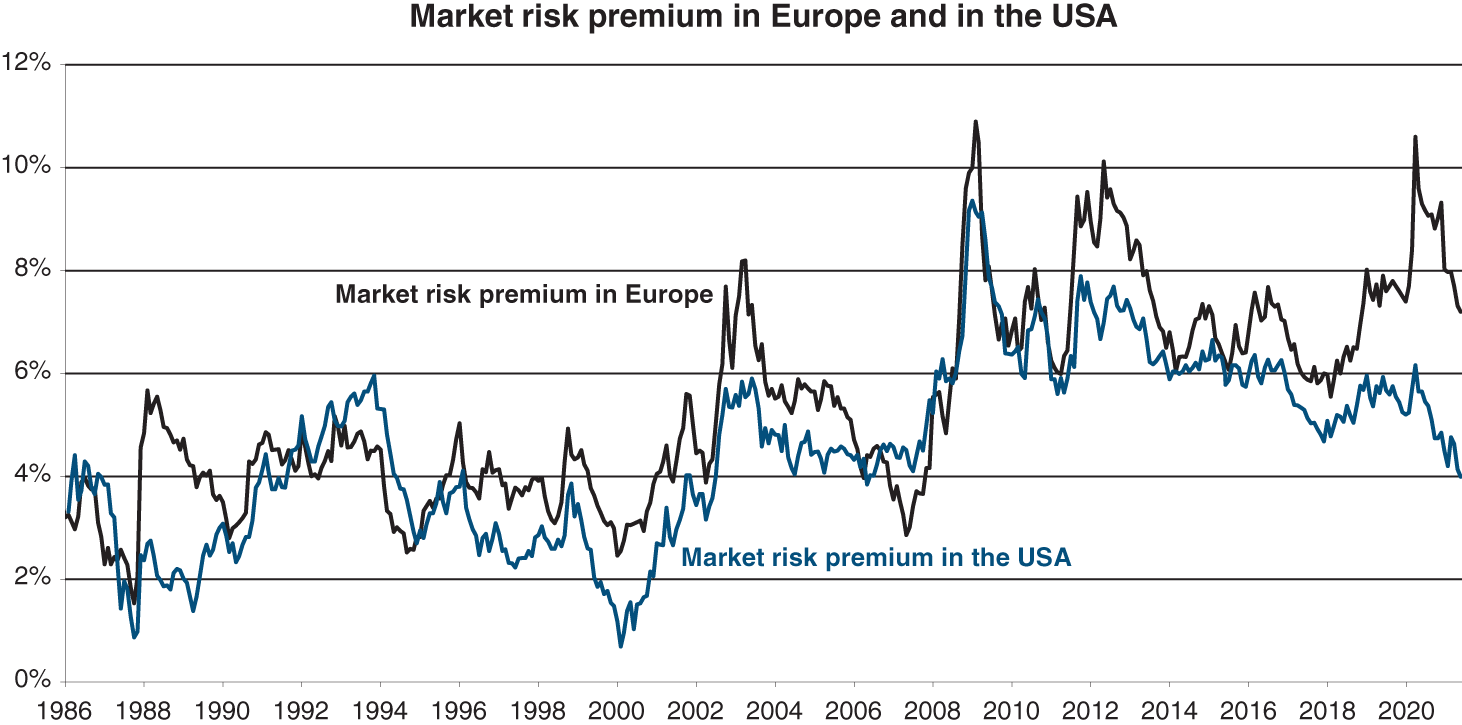
Source: Data from Associés en Finance (Europe), BNP Paribas Arbitrage & Damodaran (USA)
Over the very long term (120 years!), the historical risk premium has been as follows:
| Belgium | 3.0% | South Africa | 6.0% |
| China (1993–2020) | 4.6% | Spain | 3.3% |
| France | 5.5% | Switzerland | 3.9% |
| Germany (exc. 1922/23) | 6.2% | US | 5.8% |
| Italy | 5.6% | UK | 4.3% |
| India | 6.1% | Europe | 3.5% |
| Japan | 6.1% | World | 4.4% |
| Russia (1995–2020) | 7.4% |
Source: Crédit Suisse Global Investment Returns Yearbook, 2021. Equity risk premium compared to short-term interest rates.
The equity risk premium can be historical or expected (or anticipated). The historical risk premium is equal to the annual performance of equity markets (including dividends) minus the risk-free rate. The expected risk premium is not directly observable. However, it can be calculated by estimating the future cash flows of all the companies, and then finding the discount rate that equates those cash flows with current share prices, from which we deduct the risk-free interest rate. This expected risk premium is the one used in the CAPM.
To determine the risk premium for each stock, simply multiply the market risk premium by the stock’s beta coefficient.
Hence, if the risk-free rate is –0.5% and the expected risk premium is 8.0%, a shareholder in the French car subcontractor Valeo will expect a return of –0.5% + 1.56 × 8.00% = 12.0%, if Valeo’s β is 1.56, while a shareholder in L’Oreal will expect –0.5% + 0.70 × 8.0% = 5.1%, as L’Oreal’s β is 0.70.
Section 19.2 THE SECURITY MARKET LINE
The research house Associés en Finance publishes the securities market line3 for the entire eurozone. It is calculated on the basis of the expected return on the y-axis and the beta coefficient of each stock on the x-axis.
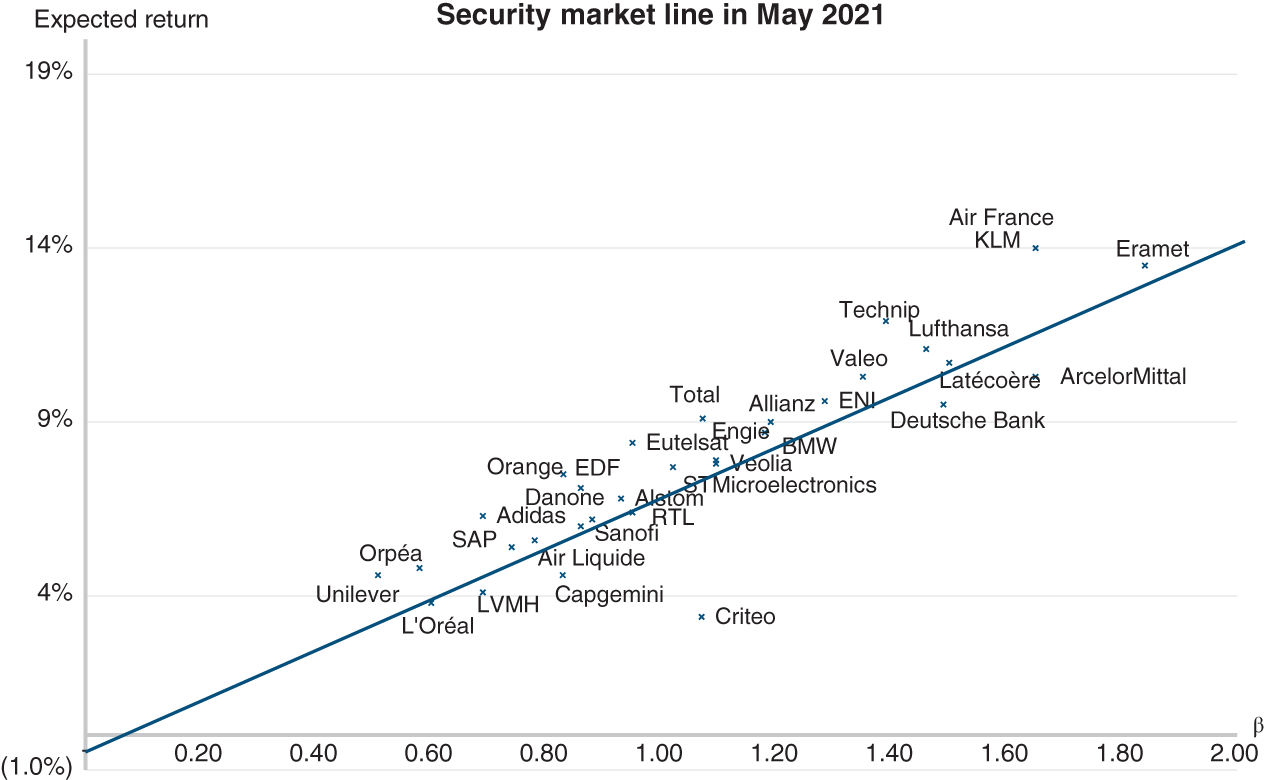
Source: Data from Associés en Finance, 2021
The securities market line is quite instructive. It helps determine the required rate of return on a security on the basis of the only risk that is remunerated, i.e. the market risk.
Shifts in the securities market line itself characterise the nature of changes in the markets and make it easier to understand them:
- a parallel shift, with no variation in slope (which represents the equity risk premium), reflects a change in interest rates. For example, a cut in interest rates normally leads to a downward shift and thus a general appreciation of all stocks;
- a non-parallel shift (or pivoting) reflects a change in the risk premium and thus in the remuneration of risk. In this case, the riskiest stocks will move the most, whereas the least risky stocks may not be significantly affected.
In addition, the position of points vis-à-vis the market line serves as a decision-making tool. The above chart tells us that Orange offers too high an expected return for its risk. Investors will realise this and buy it, thus raising its price and lowering expected return. A stock that is “above” the securities market line is thus undervalued, while a stock that is “below” the securities market line (like Adidas) is overvalued.
But do not rush to place an order. Since this chart was printed, prices have had plenty of time to adjust.
Section 19.3 LIMITS OF THE CAPM
The CAPM assumes that markets are efficient and it is without a doubt the most widely used model in modern finance. But if we wanted to be facetious, we would say that each element of the CAPM poses a practical problem!
1/ THE LIMITS OF DIVERSIFICATION
The CAPM is a development of portfolio theory and is based on the assumption that diversification helps to reduce risk reducing it to the non-diversifiable risk. A study by Campbell et al. (2001) shows that diversification is increasingly complex and that nowadays a portfolio of at least 50 stocks is required to reduce risk significantly.
This is due, among other things, to the greater volatility of individual stocks, although markets as a whole are no more volatile. Other reasons for this phenomenon are the arrival on the market of riskier companies, such as biotech, Internet and younger companies, and the near extinction of conglomerates, which, by nature, provided some diversification in and of themselves.
Meanwhile, the correlation between market return and return on individual stocks is falling. This may undermine the relevancy of the CAPM. Statistically, beta is becoming less and less relevant.
2/ DIFFICULTIES IN PRACTICAL APPLICATION OF THE CAPM
The first difficulty one encounters when using the CAPM is determining the risk-free rate which, all things considered, is just a theoretical concept.
Practitioners usually use as a risk-free rate the yield of long-term government bonds. They put forward the similar weighted average duration of the cash flows of the assets to be valued and of long-term bonds. The issue is that long-term government bonds are not without risk: their value can fluctuate in time depending on changes in interest rates (which is inevitable given the long period of time since their issue). Even investors that plan to keep government bonds until their maturity suffer from these interest rate fluctuations for the reinvestment of coupons. In addition, unanticipated changes in inflation can impact what could have appeared as a risk-free investment. Finally, there remains the solvency risk of the issuer. The increasing levels of debt of most Western countries mean that this risk is not just theoretical, as demonstrated in recent years in Greece.
Therefore, it appears more rational to use as a risk-free rate the short-term interest rate. Short-term bills are virtually not impacted by changes in interest, coupon reinvestment risk does not exist and bankruptcy risk is minor. For the Eurozone, the risk-free rate could be assessed on the basis of the return on short-term German Treasury bills.
The three key global providers of equity market risk premium data (Ibbotson, Dimson-Marsh-Staunton and Associés en Finance) propose a computation of the market risk premium based on long-term interest rates or short-term interest rates. The most important factor is not to add a short-term interest rate to a market premium computed on the basis of long-term rates, or the reverse.
Roll (1997) has pointed out that determining a market portfolio is not as easy as one would like to think. In theory, the market portfolio is not solely made up of stocks or even just financial assets, but of all the assets that can be acquired. It is therefore impossible, in practice, to come up with a true market portfolio, especially when looking at it from an international point of view.
However, we still have to determine the return expected from the market portfolio. As the CAPM is used for making forecasts, it can also be used to calculate the return expected from a security based upon the return expected from the market portfolio, as well as the security’s anticipated risk (its β). However, “anticipated” data cannot be observed directly in the market, and so forecasts must be made on the basis of historical data and macroeconomic data. For some countries, such as emerging nations, this is not easy!
3/ THE INSTABILITY OF β
The main criticism of beta is its instability over time. It boils down a large amount of information into a single figure, and this strength becomes its weakness.
The CAPM is used to make forecasts. It can be used to calculate expected return on the basis of anticipated risk. Therefore, it would be better to use a forecast β rather than a historical value, especially when the coefficient is not stable over time.
For this reason, calculations must often be adjusted to reflect the regularity of earnings and dividends, and visibility on the sector. Blume et al. (1975) have sought to demonstrate a convergence of β towards 1. This seems counterintuitive to us as some sectors will always have a beta greater than 1. In addition, the recent crisis has demonstrated that, in difficult times, the gap between high β and low β increases.
4/ THE THEORETICAL LIMITS OF CAPM AND MARKETS AT FAIR VALUE
The CAPM assumes markets are fairly valued. But markets are not necessarily always at fair value. The fact that technical analysis has become so prominent on trading floors shows that market operators themselves have doubts about market efficiency (see Chapter 18).
Moreover, the theory of efficient markets in general, and the CAPM in particular, is based on the premise that market operators have rational expectations. To be applicable, the model must be accepted by everyone as being universally correct. The development of parallel theories shows that this is not necessarily the case.
The bias mentioned above has led the CAPM to be considered as just one theoretical explanation for the functioning of the financial markets. Other theories and methods have been developed, but they have not (yet?) achieved the attractiveness of the CAPM, due to the simplicity of its concepts. We should not lose hope: a study by Ferguson and Shockley (2003) posits that all weaknesses of the CAPM could be attributable to a mis-estimation of the market portfolio and that they would disappear if not only stocks, but also bonds (and other investment opportunities), were included, as the theory suggests.
Section 19.4 MULTIFACTOR MODELS
1/ THE ARBITRAGE PRICING THEORY
In some ways the APT (arbitrage pricing theory) model is an extended version of the CAPM. The CAPM assumes that the return on a security is a function of its market risk and therefore depends on a single factor: market prices. The APT model, as proposed by Stephen Ross, assumes that the risk premium is a function of several variables, not just one, i.e. macroeconomic variables (V1, V2,…, Vn) as well as company “noise”.
So, for security J:
The model does not define which V factors are to be used. Ross’s original article uses the following factors, which are based on quantitative analyses: inflation, manufacturing output, risk premium and yield curve.
Comparing the APT model to the market portfolio, we can see that APT has replaced the notion (hard to measure in practice) of return expected by the market with a series of variables which, unfortunately, must still be determined. This is why APT is a portfolio management tool and not a tool for valuing stocks.
2/ THE FAMA–FRENCH MODEL
There are offshoots from the APT that have sought to explain historical returns by company-specific factors rather than the general macroeconomic factors in the APT.
For example, Eugene Fama and Kenneth French (1992) have isolated three factors: market return (as in the CAPM), price/book value (see Chapter 31) and the gap in returns between large caps and small caps (which lends credence to the notion of a liquidity effect).
Other factors can be added to this list, including P/E, market capitalisation, yield and even past performance (which is a direct contradiction of efficient market theory). However, these are based on purely empirical approaches, not theoretical ones. While they criticise the CAPM, they offer no better alternative model.
3/ LIQUIDITY PREMIUM, SIZE PREMIUM AND INVESTOR PROTECTION
Among the factors used in determining risk, the criteria by which liquidity can be measured (size, free float, transaction volumes, bid–ask spread) are often statistically significant. In other words, the required return on a security often appears to be a function of liquidity.
Hamon and Jacquillat (1999) have demonstrated the existence of a liquidity premium in Europe, which is nil for large caps and significant for small caps. The liquidity premium should be added to the return derived from the CAPM to arrive at the total return expected by the shareholder. Hamon and Jacquillat use the term “market plane” (instead of securities market line). Under their model, expected return on a security is a linear equation with two parameters: the market premium and the liquidity premium. Let us report the definition from the original article:
In May 2020, Associés en Finance estimated the market plane parameters for eurozone stocks at:
The liquidity premium, which is expected in addition to the required rate of return, finds its opposite number in the notion of “liquidity discount”.
Source: Data from Associés en Finance
Section 19.5 FRACTALS AND OTHER LEADS
The theory of a market in equilibrium is based on the assumption that prices have reached an equilibrium. It therefore assumes that there is an equilibrium between offer and demand and that it is reached at every moment on financial markets (thanks to the arbitrage principle). From this equilibrium, no one can predict how prices will move: they follow a random path.
Some research proposes that market prices do not follow random paths as the market in equilibrium theory predicts. In particular, extreme events (strong price growth or large drops) occur much more frequently than would be predicted by classical theory.
Several theories have been developed to model the evolution of prices and allow for possible massive price movements (in particular, crashes).
Some have tried to use chaotic functions to model prices. Chaotic here does not mean illogical or random. The term is used for perfectly predictable series of data that appear to be illogical. These models are used in a number of sciences, including economics.
Mandelbrot has put forward that fractals (or to be more precise, multi-fractals) could provide accurate representations of market price movements. This assumption does not fit with the efficient market theory, not only because the statistical rule for modelling prices is different, but more importantly because Mandelbrot’s assumptions imply that prices have memory, i.e. that they are not independent from past prices.
Section 19.6 TERM STRUCTURE OF INTEREST RATES
Because it is a single-period model, the CAPM draws no distinction between short-term and long-term interest rates. As has been discussed, a money-market fund does not offer the same annual rate of return as a 10-year bond. An entire body of financial research is devoted to understanding movements in interest rates and, in particular, how different maturities are linked. This is the study of how the yield curve, which at a point in time relates the yield to maturity to the maturity (or duration) of bonds, is formed.
1/ THE VARIOUS YIELD CURVES
By charting the interest rate for the same categories of risk at all maturities, the investor obtains the yield curve that reflects the anticipation of all financial market operators.
The concept of premium helps explain why the interest rate of any financial asset is generally proportional to its maturity.
Generally speaking, the yield curve reflects the market’s anticipation regarding:
- long-term inflation;
- the central bank’s monetary policy; and
- the issuing country’s debt management policy.
Source: Data from Datastream, Bloomberg
Source: Data from Bloomberg
Hence, during a period of economic recovery, the yield curve tends to be “normal” (i.e. long yields are higher than short yields). The steepness of the slope depends on:
- how strong an expected recovery is;
- what expectations the market has about the risk of inflation; and
- the extent to which the market expects a rapid increase in central banks’ intervention rates (to calm inflationary risks).
For the euro, the curve’s upward slope in 2021 is due to the extremely low (currently negative) levels reached by short-term rates, following European Central Bank (ECB) interventions to avoid a major economic downturn and to support the economy.
In contrast, when a recession follows a period of growth, the yield curve tends to reverse itself (with long-term rates falling below short-term rates). The steepness of the negative slope depends on:
- how strong expectations of recovery are;
- how credible the central bank’s policy is (i.e. how firm the central banks are in fighting inflation); and
- the extent to which inflationary trends appear to be diminishing (despite the recession, if inflationary trends are very strong then long-term rates will tend to remain stable, and the curve could actually be flat for some time).
This is what could be observed at the beginning of 2021 in relation to the dollar.
Lastly, when rates are low, the curve cannot remain flat for any length of time because investors will buy fixed-rate bonds. As long as investors expect that their capital gain, which is tied to falling long-term rates, is more than the cost of short-term financing, they will continue to purchase fixed-rate bonds. However, when long-term rates seem to have reached a lower limit, these expectations will disappear because investors will demand a differential between long-term and short-term rates’ yield on their investment. This results in:
- either a rebound in long-term rates; or
- stable long-term rates if short-term rates fall because of central bank policies; and
- a steepening in the curve, the degree of which will depend on the currency.
We then revert to the upward slope since the end of 2008 for the Swiss franc.
2/ RELATIONSHIP BETWEEN INTEREST RATES AND MATURITIES
By no means are short-term and long-term rates completely disconnected. In fact, there is a fundamental and direct link between them.
About 20 years ago, this relationship was less apparent and common consensus favoured the theory of segmentation, which said that supply and demand balanced out across markets, with no connection among them, i.e. the long-term bond market and the short-term bond market.
As seen above, this theory is generally no longer valid, even though each investor will tend to focus on their own timeframe. It is worthwhile reviewing the basic mechanisms. For example, an investor who wishes to invest on a two-year time basis has two options:
- invest for two years at today’s fixed rate, which is the interest rate for any two-year investment; or
- invest the funds for one year, is paid the one-year interest rate at the end of the year, and then repeat the process.
In a risk-free environment, these two investments would produce the same return, as the investor would already know the return that they would be offered on the market in one year for a one-year bond. As they also know the current one-year rate, they can determine the return on a two-year zero-coupon bond.
where 0r2 is the current two-year rate, 1r1 the one-year rate in one year and 0r1 the current one-year rate.
Hence:
If today the one-year interest rate is 3% and the two-year interest rate is 4%, this means that the market expects the one-year interest rate to reach 5% in one year, as
An increase in short-term rates is then anticipated by the market.
In such a world, the shape of the yield curve provides some valuable information. For example, if long-term rates are higher than short-term rates, this necessarily implies that investors are anticipating an increase in interest rates.
This theory assumes that investors are not sensitive to risk and therefore that there is no preference for a short-term or a long-term investment. This does not deal with the attention that investors pay to liquidity, as demonstrated by recent events on financial markets.
3/ TAKING LIQUIDITY INTO CONSIDERATION
The first theories to highlight the existence of a premium to reflect the relative lack of liquidity of long-term investments were the preferred habitat theory and the liquidity preference theory.
In the mid-1960s, Modigliani and Sutch advanced the theory of preferred habitat, which says that investors prefer certain investment timeframes. Companies that wish to issue securities whose timeframe is considered undesirable will thus have to pay a premium to attract investors.
The theory of liquidity preference is based on the same assumption, but goes further in assuming that the preferred habitat of all investors is the short term. Investors preferring liquidity will require a liquidity premium if they are to invest for the long term.
Even if investors anticipate fixed short-term rates, the yield curve will slope upward due to the liquidity premiums.
4/ YIELD CURVES AND VALUATION OF SECURITIES
After having studied the yield curve, it is easier to understand that the discounting of all the cash flows from a fixed-income security at a single rate, regardless of the period when they are paid, is an oversimplification, although this is the method that will be used throughout this text for stocks and capital expenditure. It would be wrong to use it for bonds.
In order to be more rigorous, it is necessary to discount each flow with the interest rate of the yield curve corresponding to its maturity: the one-year rate for next year’s income stream, the three-year rate for flows paid in three years, etc. Ultimately, yield to maturity is similar to an average of these different rates.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTES
- 1 However, the very fact that the entrepreneur does not diversify their portfolio means that they must achieve strong performances in managing their company, as they have everything to lose. So they are likely to take steps to reduce risk.
- 2 For the risk-free rate, kF is equal to rF. The required rate of return is equal to the return that is actually received, as the asset has no risk.
- 3 It differs from the capital market line, which has the total risks of the security on the x-axis, not the β coefficient.
****PART THREE. FINANCIAL SECURITIES
There is a great variety of financial instruments, each of which has the following characteristics:
- it is a contract …
- … executed over time, and …
- its value derives solely from the series of cash flows it represents.
Indeed, from a mathematical and more theoretical viewpoint, a financial instrument is defined as a schedule of future cash flows.
Holding a financial security is the same as holding the right to receive the cash flows, as defined in the terms and conditions. Conversely, for the issuer, creating a financial instrument is the same as committing to paying out a series of cash flows. In return for this right to receive cash flows or for taking on this commitment, the company will issue a security at a certain price, enabling it to raise the funds needed to run its business.
You’ve undoubtedly heard people say that the financial manager’s stock-in-trade is “paper”. Digitalisation has now turned financial instruments from paper documents into intangible book entries, reducing them to the information they contain, i.e. the contract. The essence of finance is, and will always be, negotiation between an issuer seeking new funds and the investors interested in buying the instruments that represent the underlying obligations. And negotiation means markets, be they credit markets, bond markets, stock markets, etc.
Time, or the term of the financial security, introduces the notion of time remuneration and risk. A debt instrument that promises cash flows over time, for example, entails risk, even if the borrower is very creditworthy. This seems strange to many people who consider that “a deal is a deal” or “a person’s word is their bond”. Yet, experience has shown that a wide variety of risks can affect the payment of those cash flows, including political risk, strikes, natural disasters, pandemics and other events.
The financial logic that we have seen in the previous chapters is used to analyse and choose among a firm’s investment options. The financial manager transforms flows of goods and services, deriving from the company’s industrial and other business assets, into cash flows. You will soon understand that the world of finance is one of managing rights on the one hand and commitments on the other, both expressed in terms of cash flows.
In a market for financial instruments, it is not the actual flows that are sold, but the rights associated with them. The investor, i.e. the buyer of the security, acquires the rights granted by the instrument. The issuing company assumes contractual obligations deriving from the instrument, regardless of who the owner of the instrument is.
For example, commodity futures markets make it possible to perform purely financial transactions. You can buy sugar “forward”, via financial instruments called futures contracts, knowing full well that you will never take delivery of the sugar into your warehouse. Instead, you will close out the position prior to maturity. The financial manager thus trades on a market for real goods (sugar), using contracts that can be unwound prior to or at maturity.
A property investor acts similarly. After acquiring real property, the value of which fluctuates, they can lease it or resell it. Viewed this way, real property is as fungible as any other property and is akin to a financial asset.
Clearly, these assets exhibit different degrees of “financiality”. To take the argument one step further, you turn a painting into a financial instrument when you put it in your safe in the hope of realising a gain when you sell it.
The distinction between a real asset and a financial asset is therefore subtle but fundamental. It lies either in the nature of the contract or in the investor’s motivation, as in the example of the painting.
Lastly, the purchase of a financial security differs from the purchase of a durable good in that the financial security is undifferentiated. A large number of investors can buy the same financial security. In contrast, acquiring a specific office building or building an industrial plant is a very specific, unique investment.
Chapter 20. BONDS
Fixing the interest
Unlike equity, for which shares are the legal form of the security, bank and financial debt can take the form of bank loans or debt securities. The predominant form of debt securities is a bond.
A debt security is a financial instrument representing the borrower’s obligation to the lender from whom they have received funds. If the initial maturity of the security is over one year, it will be called a bond.
This obligation provides for a schedule of cash flows defining the terms of repayment of the funds and the lender’s remuneration in the interval. The remuneration may be fixed during the life of the debt or floating if it is linked to a benchmark or index.
Unlike conventional bank loans, debt securities can be traded on secondary markets (stock exchanges, money markets, mortgage markets, interbank markets, over the counter (OTC) markets). Other than this, their logic remains the same and all the reasoning presented in this chapter also applies for bank loans. Debt securities are bonds, commercial paper, Treasury bills and notes, certificates of deposit and mortgage-backed bonds or mortgage bonds. Furthermore, the current trend is to securitise loans to make them negotiable.
Disintermediation was not the only factor fuelling the growth of bond markets. The increasing difficulty of obtaining bank loans was another, as banks realised that the interest margin on such loans did not offer sufficient return on equity. This pushed companies to turn to bond markets to raise the funds that banks had become reluctant to advance. The increasingly burdensome solvency and liquidity constraints imposed on banks (Basel III and IV) has increased the share of financing insured by the debt capital markets even further (see Chapter 39).
Investors have welcomed the emergence of corporate bonds offering higher yields than government bonds. Of course, these higher returns come at the cost of higher risks.
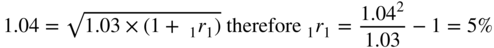
Source: Data from BNP Paribas
Many of the explanations and examples offered in this chapter deal with bonds, but they can easily be applied to all kinds of debt instruments. We shall take the example of the Ahold Delhaize 2030 bond issue with the following features:
Section 20.1 BASIC CONCEPTS
1/ THE PRINCIPAL
(a) Nominal or face value
Loans that can be publicly traded are divided into a certain number of units giving the same rights for the same fraction of the debt. The nominal, face or par value is €100,000 in the Ahold Delhaize case.
The nominal value is used to calculate the interest payments. In the simplest cases (which is not the case for Ahold Delhaize), it equals the amount of money the issuer received for each bond and that the issuer will repay upon redemption.
(b) Issue price
The issue price is the price at which the bonds are issued; that is, the price investors pay for each bond. The Ahold Delhaize bond was issued on 18 March 2021 at a price of €99,630, i.e. 99.63% of its face value.
Depending on the characteristics of the issue, the issue price may be higher than the face value (issued at a premium), lower than the face value (issued at a discount) or equal to the face value (at par).
(c) Redemption
When a loan is amortised, it is said to be redeemed. In Chapter 17 we looked at the various ways a loan can be repaid:
- redemption at maturity, or on a bullet repayment basis. This is the case in the Ahold Delhaize issue;
- redemption in equal slices (or series), or constant amortisation;
- redemption in fixed instalments.
Other methods exist, such as determining which bonds are redeemed by lottery… there is no end to financial creativity!
A deferred redemption period is a grace period, generally at the beginning of the bond’s life, during which the issuer does not have to repay the principal.
The terms of the issue may also include provisions for early redemption (call options) or retraction (put options). A call option (see Chapter 23) gives the issuer the right to buy back all or part of the issue prior to the maturity date, while a put option allows the bondholder to demand early repayment.
A redemption premium or discount arises where the redemption value is higher or lower than the nominal value.
(d) Maturity of the bond
The life of a bond extends from its issue date to its final redemption date. Where the bond is redeemed in several instalments, the average maturity of the bond corresponds to the average of each of the repayment periods.
The Ahold Delhaize bonds have a maturity of nine years.
(e) Guarantees
Repayment of the principal (and interest) on a bond borrowing can be guaranteed by the issuer, the parent company and less often for corporates by collateral (i.e. mortgages), pledges or warranties. Bonds are rarely secured, while commercial paper and certificates of deposit can, in theory, be secured but in fact never are.
The bonds issued by Ahold Delhaize do not benefit from a guarantee.
2/ INCOME
(a) Issue date
The issue date is the date on which interest begins to accrue. It may or may not coincide with the settlement date, when investors actually pay for the bonds purchased.
In the case of the Ahold Delhaize bond, these two dates coincide. Interest begins to accrue on the settlement date.
(b) Interest rate
The coupon or nominal rate is used to calculate the interest (or coupon, in the case of a bond) payable to the lenders. Interest is calculated by multiplying the nominal rate by the nominal or par value of the bond.
On the Ahold Delhaize issue, the coupon rate is 0.375% and the coupon payment is €375. However, if Ahold Delhaize did not reduce its carbon emissions by 29% between 2018 and 2025 (scope 1 and 2) and its food waste (discarded food) by 32% between 2016 and 2025, then the annual coupon would increase to €625. This provision makes this bond a sustainable one.
In addition to coupon payments, investors may also gain additional remuneration if the issue price is lower than the par value (which is the case for Ahold Delhaize). This is the issuance premium. If the issue price is higher than the par value, the lender’s return will be lower than the coupon rate.
(c) Periodicity of coupon payments
Coupon payments can be made every year, half-year, quarter, month or even more frequently. On certain borrowings, the interval is longer, since the total compounded interest earned is paid only upon redemption. Such bonds are called zero-coupon bonds.
In some cases, the interest is prepaid; that is, the company pays the interest at the beginning of the period to which it relates. In general, however, the accrued interest is paid at the end of the period to which it relates.
The Ahold Delhaize issue pays accrued interest on an annual basis.
Section 20.2 THE YIELD TO MATURITY
The actual return on an investment (or the cost of a loan for the borrower) depends on a number of factors: the difference between the settlement date and the issue date, the issue premium/discount, the redemption premium/discount, the deferred redemption period and the coupon payment interval. As a result, the nominal rate is not very meaningful.
We have seen that the yield to maturity (Chapter 17) cancels out the bond’s present net value; that is, the difference between the issue price and the present value of future flows on the bond. Note that for bonds, the yield to maturity (y) and the internal rate of return are identical. This yield, calculated on the settlement date when investors pay for their bonds, takes into account any timing differences between the right to receive income and the actual cash payment.
In the case of the Ahold Delhaize bond issue:
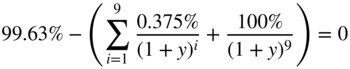
i.e. y = 0.417%. The yield to maturity, before taxation and intermediaries’ fees, represents:
- for investors, the rate of return they would receive by holding the bonds until maturity, assuming that the interest payments are reinvested at the same yield to maturity, which is a very strong assumption;
- for the issuer, the pre-tax actuarial cost of the loan.
From the point of view of the investor, the bond schedule must take into account intermediation costs and the tax status of the income earned. For the issuer, the gross cost to maturity is higher because of the commissions paid to intermediaries. This increases the actuarial cost of the borrowing. In addition, the issuer pays the intermediaries (paying agents) in charge of paying the interest and reimbursing the principal (generally between 0.2 and 0.4% on the Euro Investment Grade market). Lastly, the issuer can deduct the coupon payments in whole or in part to compute its corporate income tax, thus reducing the actual cost of the loan.
1/ SPREADS
The spread is the difference between the rate of return on a bond and that on a benchmark used by the market. In the eurozone, the benchmark for long-term debt is most often the interest rate swap (IRS) rate1; sometimes the spread to government bond yields is also mentioned. For floating-rate bonds and bank loans (which are most often with floating rates), the spread is measured to a short-term rate, the three- or six-month Euribor in the eurozone.
The Ahold Delhaize bond was issued with a spread of 41 basis points (0.41%) to mid swap rate, meaning that Ahold Delhaize had to pay 0.41% more per year than the risk-free rate to raise funds.
The spread is a key parameter for valuing bonds, particularly at the time of issue. It depends on the perceived credit quality of the issuer and the maturity of the issue, which are reflected in the credit rating and the guarantees given. Spreads are, of course, a relative concept, depending on the bonds being compared. The stronger the creditworthiness of the issuer and the market’s appetite for risk, the lower the margin will be.
2/ THE SECONDARY MARKET
Once the subscription period is over, the price at which the bonds were sold (their issue price) becomes a thing of the past. The value of the instrument begins to fluctuate on the secondary market. Consequently, the yield to maturity published in the prospectus applies only at the time of issue; after that, it fluctuates in step with the value of the bond. Note that, as with equity issues, there is usually a small increase in the price of bonds just after they are issued (the price is said to be tightening). New issues usually offer a small yield premium (new issue premium)
Theoretically, changes in the bond’s yield to maturity on the secondary market do not directly concern the borrower, since the cost of the debt was fixed when it was contracted.
Source: Data from Datastream/Factset
Source: Data from Datastream/Factset
For the borrower, the yield on the secondary market is merely an opportunity cost; that is, the cost of refunding for issuing new bonds. It represents the “real” cost of debt, but is not shown in the company accounts where the debt is recorded at its historical cost, regardless of any fluctuations in its value on the secondary market. The market value of debt can only be found in the notes to IFRS accounts.
3/ LISTING TECHNIQUES
The price of bonds listed on stock markets is expressed as a percentage of the nominal value. In fact, they are treated as though the nominal value of each bond were €100. Thus, a bond with a nominal value of €50,000 will not be listed at €49,500 but at 99% (49,500 / 50,000 × 100). Similarly, a bond with a nominal value of €10,000 will be listed at 99%, rather than €9,900. This makes it easier to compare bond prices.
For the comparison to be relevant, the prices must not include the fraction of annual interest already accrued. Otherwise, the price of a bond with a 5% coupon would be 105 just before its coupon payment date and 100 just after. This is why bonds are quoted net of accrued interest. Bond tables thus show both the price expressed as a percentage of the nominal value and the fraction of accrued interest, which is also given as a percentage of the nominal value.
On 5 May 2021, the Ahold Delhaize bond traded at 99.2% with 0.042% accrued interest. Buying the Ahold Delhaize bond then would have cost (excl. any trading fee or tax) €99,242: €100,000 × (99.2% + 0.042%).
Certain debt securities, mainly fixed-rate Treasury notes with annual interest payments, are quoted at their yield to maturity.
By now you have probably realised that the price of a bond does not reflect its actual cost. A bond trading at 105% may be more or less expensive than a bond trading at 96%. The yield to maturity is the most important criterion, allowing investors to evaluate various investment opportunities according to the degree of risk they are willing to accept and the length of their investment. However, it merely offers a temporary estimate of the promised return; this may be different from the expected return, which incorporates the probability of default of the bond.
4/ FURTHER ISSUES AND ASSIMILATION
Having made one bond issue, the same company can later issue other bonds (informally, this is called a tap issue) with the same features (time to maturity, coupon rate, coupon payment schedule, redemption price and guarantees, etc.), so that they are interchangeable. This enables the various issues to be grouped as one for a larger total amount. Assimilation makes it possible to reduce administrative expenses and enhance liquidity on the secondary market.
Nevertheless, the drawback for the issuer is that it concentrates maturity on one date, which is not in line with sound financial policy.
Bonds assimilated are issued with the same features as the bonds with which they are interchangeable. The only difference is in the issue price,2 which is shaped by market conditions that are very likely to have changed since the original issue.
Section 20.3 FLOATING-RATE BONDS
So far we have looked only at fixed-income debt securities. The cash flow schedule for these securities is laid down clearly when they are issued. These are very popular in periods of low interest rates, and currently represent 84% of euro-denominated bond issues. Let us now cover the various securities that give rise to cash flows that are not totally fixed from the very outset, but follow preset rules (10% of all bond issuances in 2020).
1/ THE MECHANICS OF THE COUPON
The coupon of a floating-rate bond (floating rate note, FRN or “floats”) is not fixed, but is indexed to an observable market rate, generally a short-term rate, such as a six-month Euribor. In other words, the coupon rate is periodically reset based on some reference rate plus a spread. When each coupon is presented for payment, its value is calculated as a function of the market rate, based on the formula:
This cancels out the interest rate risk, since the issuer of the security is certain of paying interest at exactly the market rate at all times. Likewise, the investor is assured at all times of receiving a return in line with the market rate. Consequently, there is no reason for the price of a variable-rate bond to move very far from its par value unless the issuer’s solvency changes.
2/ INDEX-LINKED SECURITIES
Floating rates, as described in the first paragraph of this section, are indexed to a market interest rate. Broadly speaking, however, a bond’s coupons may be indexed to any index or price provided that it is clearly defined from a contractual standpoint. Such securities are known as index-linked securities.
For instance, most European countries have issued bonds indexed to inflation. The coupon paid each year, as well as the redemption price, is reset to take into account the rise in the price index since the bond was launched. As a result, the investor benefits from complete protection against inflation. Likewise, Mexican companies have brought to market bonds linked to oil prices, while other companies have issued bonds indexed to their own share price.
The following table shows the main reference rates in Europe.
REFERENCE RATES IN EUROPE
| Reference rate | Definition | As at April 2021 |
|---|---|---|
| EONIA (Euro Overnight Index Average) | Traditional European money-market rate. Since end 2019 it is computed as €STR +8.5 basis points. It should disappear end 2021 and be replaced by €STR. | −0.42% |
| €STR (European Short-Term Rate) | The new European money-market rate that replaces EONIA. It is an interest rate computed based on real loans and not only declared loans as was EONIA. | –0.56% |
| EURIBOR (European Interbank Offered Rate) | European money-market rate corresponding to the arithmetic mean of offered rates on the European banking market for a given maturity (between 1 week and 12 months). Sponsored by the European Banking Federation and published by Reuters, it is based on daily quotes provided by 43 European banks. | −0.53% (3 months) |
| LIBOR (London Interbank Offered Rate) | Money-market rate observed in London corresponding to the arithmetic mean of offered rates on the London banking market for a given maturity (between 1 and 12 months) and a given currency (euro, sterling, dollar, etc.). It will be replaced in 2021/2022 by ECB RFR (€), SONIA (£) and SOFR ($). | −0.54% (euro 3 months) |
| IRS | The IRS rate indicates the fixed interest rate that will equate the present value of the fixed-rate payments with the present value of the floating-rate payments in an interest rate swap contract. The convention in the market is for the swap market makers to set the floating leg – normally at Euribor – and then quote the fixed rate that is payable for that maturity. |
Section 20.4 GREEN AND SOCIALLY RESPONSIBLE BONDS
Responsible bonds include three categories of bonds that are, in terms of their financial flows, conventional bonds, but which incorporate ESG aspects.
The issuer of green bonds commits to use the funds for environmentally positive investments or expenditures (as defined by the company, usually assisted by an independent firm).
Tracking expenditure and allocating a funding source to a particular job requires a specific organisation that is unusual for finance management. This organisation has a cost. However, as investors have been willing to buy green bonds at a slightly higher price than a conventional bond since autumn 2020, the so-called greenium, the extra cost is more or less offset for companies. Green bonds are, even if companies sometimes deny it, a communication tool but also a means of internal mobilisation. Paradoxically, many green bond issuers operate in industries whose ecological character is not immediately obvious: energy (EDF, Engie), automotive (Toyota). Some have therefore launched the concept of transition bonds, which are bonds that specifically finance the energy transition.
The volume of green bond issues is growing very quickly, but remains modest (€265bn in 2020) compared to the bond market (around 5%).
Social bonds finance projects with a social connotation. For example, Icade issued a €600m social bond in 2020 to facilitate access to healthcare for all. This is a €130bn market where the share of companies is structurally low (a few billion euros of issues per year).
Since the autumn of 2020, sustainable bonds (or sustainability-linked bonds, SLBs) have experienced very strong growth driven by companies that, because of their sector of activity, do not necessarily have investments to make in the energy transition or quantifiable social objectives requiring heavy investments. In contrast to green or social bonds, which are qualified as such because of the use of funds, sustainable bonds can be used for any purpose. Their sustainability comes from the interest rate they pay to lenders, which can be increased if they do not meet quantified ESG targets, normally ambitious ones, that they have set themselves: reducing greenhouse gas emissions, increasing recycling, switching to 100% renewable electricity, increasing the proportion of women in management teams, training disadvantaged people in energy management, etc. Ahold Delhaize’s obligation is a sustainable obligation.
As with green bonds, the green premium (the greenium) increases, making this form of financing cheaper than a conventional bond, at least as long as the company is able to meet its ESG objectives. The relatively small sustainable bond market (around €70bn in 2020) will clearly continue to grow strongly in the future and could become the norm for companies.
As evidence of the growth of this market, the principles of these issues are now standardised in the Green Bonds Principles (GBP), the Social Bond Principles (SBP) and the Sustainability-Linked Bond Principles (SLBP).
Section 20.5 THE VOLATILITY OF DEBT SECURITIES
The holder of a debt security may have regarded themself as protected having chosen this type of security, but they actually face three types of risk:
- interest rate risk and coupon reinvestment risk, which affect almost solely fixed-rate securities;
- credit risk, which affects fixed-rate and variable-rate securities alike. We will consider this at greater length in the following section.
1/ CHANGES IN THE PRICE OF A FIXED-RATE BOND CAUSED BY INTEREST RATE FLUCTUATIONS
(a) Definition
What would happen if, at the end of the subscription period for the Ahold Delhaize 0.375% bond, the market interest rate rose to 0.875% (scenario 1) or fell to 0% (scenario 2)? In the first scenario, the bondholder would obviously attempt to sell the Ahold Delhaize bond to buy securities yielding 0.875%. The price of the bond would fall such that the bond offered its buyer a yield to maturity of 0.875%. Conversely, if the market rate fell to 0%, holders of the Ahold Delhaize bond would hold onto their bonds, which yield 0.375%, while the market interest rate for the same risk level is now 0%. Other investors would attempt to buy them, and the price of the bond would rise to a level at which the bond offered its buyer a yield to maturity of 0%.
An upward (or downward) change in interest rates therefore leads to a fall (or rise) in the present value of a fixed-rate bond, irrespective of the issuer’s financial condition.
As we have seen, if the yield on our Ahold Delhaize bond is 0.375%, its price is 100%.
But if its yield to maturity rises to 0.875% (a 0.5 point increase or 50 basis points), its price will change to:
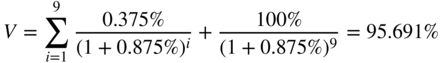
i.e. a decrease of 4.3%. This shows that holders of bonds face a risk to their capital, and this risk is by no means merely theoretical, given the fluctuations in interest rates over the medium term.
Source: Data from Datastream/Bank of England
(b) Measures: modified duration and convexity
The modified duration of a bond measures the percentage change in its price for a given change in interest rates. The price of a bond with a modified duration of 4 will increase by 4% when interest rates fall from 7% to 6%, while the price of another bond with a modified duration of 3 will increase by just 3%.
From a mathematical standpoint, modified duration can be defined as the absolute value of the first derivative of a bond’s price with respect to interest rates, divided by the price:
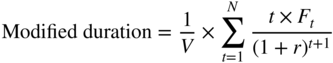
where r is the market rate and Ft the cash flows generated by the bond.
Turning back to the example of the Ahold Delhaize bond at its issuance date, we arrive at a modified duration of 8.83.
Modified duration is therefore a way of calculating the percentage change in the price of a bond for a given change in interest rates. It simply involves multiplying the change in interest rates by the bond’s modified duration. A rise in interest rates from 0.375% to 0.875% therefore leads to a price decrease of 0.5% × 8.83 = 4.41%, i.e. from 100% to 100 × (1 − 4.41%) = 95.59%.
We note a discrepancy of 0.101% with the price calculated previously (95.691%). Modified duration is valid solely at the point where it is calculated (i.e. 0.417% here). The further we move away from this point, the more skewed it becomes. For instance, at a yield of 0.875% it is 8.79 rather than 8.83. This will skew calculation of the new price of the bond, but the distortion will be small if the fluctuation in interest rates is also limited in size. From a geometrical standpoint, the modified duration is the first derivative of price with respect to interest rates and it reflects the slope of the tangent to the price/yield curve. Since this forms part of a hyperbolic curve, the slope of the tangent is not constant and moves in line with interest rates.
(c) Parameters influencing modified duration
Let’s consider the following three bonds:
| Bond | A | B | C |
|---|---|---|---|
| Coupon | 5% | 5% | 0% |
| Price | 100 | 100 | 100 |
| Yield to maturity | 5% | 5% | 5% |
| Redemption price | 100 | 100 | 432.2 |
| Residual life | 5 years | 15 years | 30 years |
How much are these bonds worth in the event of interest rate fluctuations?
| Market interest rates (%) | A | B | C |
|---|---|---|---|
| 1 | 119.4 | 155.5 | 320.7 |
| 5 | 100 | 100 | 100 |
| 10 | 81.0 | 62.0 | 24.8 |
| 15 | 66.5 | 41.5 | 6.5 |
Note that the longer the maturity of a bond, the greater its sensitivity to a change in interest rates.
Modified duration is primarily a function of the maturity date. The closer a bond gets to its maturity date, the closer its price moves towards its redemption value and the more its sensitivity to interest rates decreases. Conversely, the longer it is until the bond matures, the greater its sensitivity to interest rate fluctuations.
Modified duration also depends on two other parameters, which are nonetheless of secondary importance to the time-to-maturity factor:
- the bond’s coupon rate: the lower the coupon rate, the higher its modified duration;
- market rates: the lower the level of market rates, the higher a bond’s modified duration.
Modified duration represents an investment tool used systematically by fixed-income portfolio managers. If they anticipate a decline in interest rates, they opt for bonds with a higher modified duration, i.e. a longer time to maturity and a very low coupon rate, or even zero-coupon bonds, to maximise their capital gains.
Conversely, if portfolio managers expect a rise in interest rates, they focus on bonds with a low modified duration (i.e. due to mature shortly and carrying a high coupon) in order to minimise their capital losses.
Convexity is the second derivative of price with respect to interest rates. It measures the relative change in a bond’s modified duration for a small fluctuation in interest rates. Convexity expresses the speed of appreciation or the sluggishness of depreciation in the price of the bond if interest rates decline or rise.
2/ COUPON REINVESTMENT RISK
As we have seen, the holder of a bond does not know at what rate its coupons will be reinvested throughout the bond’s lifetime. Only zero-coupon bonds afford protection against this risk, simply because they do not carry any coupons!
First of all, note that this risk factor is the mirror image of the previous one. If interest rates rise, then the investor suffers a capital loss but is able to reinvest coupon payments at a higher rate than the initial yield to maturity. Conversely, a fall in interest rates leads to a loss on the reinvestment of coupons and to a capital gain.
Intuitively, it seems clear that for any fixed-income debt portfolio or security, there is a period over which:
- the loss on the reinvestment of coupons will be offset by the capital gain on the sale of the bond if interest rates decline;
- the gain on the reinvestment of coupons will be offset by the capital loss on the sale of the bond if interest rates rise.
All in all, once this period ends, the overall value of the portfolio (i.e. bonds plus reinvested coupons) is the same, and the investors will have achieved a return on investment identical to the yield to maturity indicated when the bond was issued.
In such circumstances, the portfolio is said to be immunised, i.e. it is protected against the risk of fluctuations in interest rates (capital risk and coupon reinvestment risk). This time period is known as the duration of a bond. It may be calculated at any time, either at issue or throughout the whole life of the bond.
For instance, an investor who wants to be assured of achieving a certain return on investment over a period of three years will choose a portfolio of debt securities with a duration of three years.
Note that the duration of a zero-coupon bond is equal to its remaining life.
In mathematical terms, duration is calculated as follows:
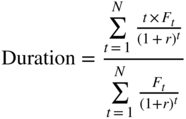
Duration can be regarded as being akin to the discounted average life of all the cash flows of a bond (i.e. interest and capital). The numerator comprises the discounted cash flows weighted by the number of years to maturity, while the denominator reflects the present value of the debt.
The Ahold Delhaize bond has a duration of 8.86 years at issue.
We can see that 8.83 × (1 + 0.417%) = 8.86 years.
Turning our attention back to modified duration, we can say that it is explained by the duration of a bond, which brings together in a single concept the various determinants of modified duration, i.e. time to maturity, coupon rate and market rates.
Section 20.6 DEFAULT RISK AND THE ROLE OF RATING
Default risk can be measured on the basis of a traditional financial analysis of the borrower’s situation or by using credit scoring, as we saw in Chapter 8. Specialised agencies, which analyse the risk of default, issue ratings that reflect the quality of the borrower’s signature. There are three agencies that dominate the market – Standard & Poor’s, Moody’s and Fitch – but with the rise of a debt capital market for mid-sized companies, new rating agencies have emerged (e.g. Spread Research, Scope Credit Rating, or Egan-Jones).
Rating agencies provide ratings for companies, banks, sovereign states and municipalities. They can decide to rate a specific issue or to give an absolute rating for the issuer (rating given to first-ranking debt). Rating agencies also distinguish between short- and long-term prospects.
Some examples of short-term debt ratings:
| Moody’s | Standard & Poor’s and Fitch | Definition | Examples (May 2021) |
|---|---|---|---|
| Prime 1 | A–1 | Superior ability to meet obligations | Sanofi, Nestlé, France |
| Prime 2 | A–2 | Strong ability to repay obligations | Iberdrola, Deutsche Bank |
| Prime 3 | A–3 | Acceptable ability to repay obligations | Morocco, ArcelorMittal |
| Not Prime | B | Speculative | Senegal, Lufthansa |
| C | Vulnerable | Argentina | |
| D | Insolvent | Venezuela, Lebanon |
Some examples of long-term debt ratings:
| Moody’s | Standard & Poor’s and Fitch | Definition | Examples (May 2021) |
|---|---|---|---|
| Aaa | AAA | Best quality, lowest risk | Germany, Australia Johnson & Johnson, Microsoft |
| Aa | AA | High quality. Very strong ability to meet payment obligations | Nestlé, Sanofi, Apple, France |
| A | A | Upper-medium grade. Issuer has strong capacity to meet its obligations | BASF, BNP Paribas, LVMH, Unilever |
| Baa | BBB | Medium grade. Issuer has satisfactory capacity to meet its obligations | Morocco, Italy, Telefónica, Pernod Ricard |
| Ba | BB | Speculative. Uncertainty of issuer’s capacity to meet its obligations | Renault, Attijariwafa Bank, Vietnam |
| B | B | Issuer has poor capacity to meet its obligations | Casino, Pakistan |
| Caa | CCC | Poor standing. Danger with respect to payment of interest and return of principal | CGG, Democratic Republic of Congo |
| Ca | CC | Highly speculative. Often in default | Belize |
| C | C | Close to insolvency | |
| D or SD | Insolvent! | Vallourec, Lebanon |
Rating services also add an outlook to the rating they give – stable, positive or negative – which indicates the likely trend of the rating over the two to three years ahead.
Short- and medium-term ratings may be modified by a + or − or a numerical modifier, which indicates the position of the company within its generic rating category. This is referred to as a notch, such as between AA– and A+. The watchlist alerts investors that an event such as an acquisition, disposal or merger, once it has been weighed into the analysis, is likely to lead to a change in the rating. A company on the watchlist is likely to be upgraded when the expected outcome is positive, downgraded when the expected outcome is negative and, when the agency is unable to determine the outcome, it indicates an unknown change.
The term split rating is used when several rating agencies evaluate the same company and do not give equivalent ratings (Ba+ and BBB– for example).
Ratings between AAA and BBB− are referred to as investment grade, and those between BB+ and D as speculative grade (or non-investment grade). The distinction between these two types of risk is important to investors, especially institutional investors, who often are not permitted to buy the risky speculative grade bonds!
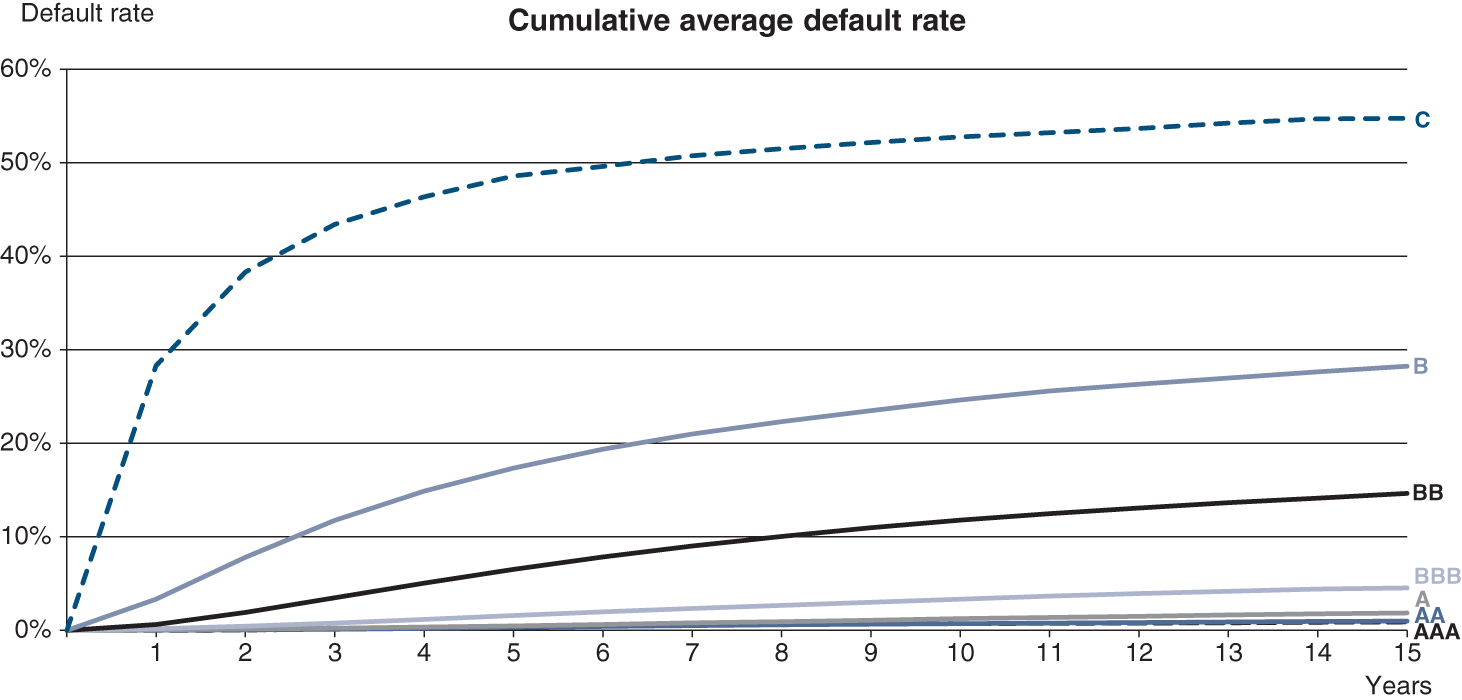
Source: Data from Standard & Poor’s 2020
Bonds at the edge of the investment grade frontier, rated BB+/BB are called crossover bonds. This is an intermediate category that links the investment grade and non-investment grade categories. Depending on the state of the market, the definition of cross-over can vary and even include companies rated BB– in well-oriented markets.
In Europe, rating agencies generally rate companies at their request, which enables them to access privileged information (medium-term plans, contacts with management). Rating agencies very rarely rate companies without management cooperation. When they do, the accuracy of the rating depends on the quality of the information about the company available on the market. If the company does not require a public rating immediately (or if it does not like the rating allocated!), it may request that it be kept confidential, and it is then referred to as a shadow rating. The cost for a firm to get a first rating is quite high (over €500,000 on average, to which should be added an annual cost of over €100,000).
The rating process, which can take up to three months, differs from the scoring process as it is not only a quantitative analysis. The agency will also take into account:
- the size of the company
- the positioning of the company in its sector;
- the analysis of the financial data;
- the current capital structure but also the financing strategy.
Most rating agencies have developed teams capable of assessing the ESG aspects of an issuer or bond, or even acquired specialised agencies such as Vigeo Eiris acquired by Moody’s.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTES
Chapter 21. OTHER DEBT PRODUCTS
Chapter 21
OTHER DEBT PRODUCTS
What a choice!
In the previous chapter, we first presented the bond as a debt product and we illustrated the key features of a debt product through this simple security. The reader will now discover that there are actually a very large number of products that follow the same logic as that of a bond: remuneration independent from the financial performance of the firm, a commitment to reimburse, and in the event of insolvency: priority over equity in the reimbursement of the money owed.
Whether short, medium or long term, market or bank, these instruments increasingly have an ESG dimension either through the use of proceeds or through an interest rate whose level depends on the achievement of environmental, social or governance objectives, such as the sustainable bonds presented in the previous chapter. These are known as green loans and impact loans.
Section 21.1 MARKETABLE DEBT SECURITIES
1/ SHORT-TERM MARKETABLE SECURITIES
The term bond (see previous chapter) is used to refer to marketable securities with maturity of over one year, but firms can also issue shorter-term instruments. Commercial paper refers to negotiable debt securities issued on the money market by large (and now medium-sized) companies for periods ranging from one day to one year. In practice, the average maturity of commercial paper is very short, between one and three months. Issuers can also launch paper denominated in foreign currency.
Short-term European paper (STEP) has homogenised the documentation for the issue of short-term paper in Europe.
Obtaining at least a short-term credit rating for a commercial paper issue is optional but implicitly recommended, since companies are required to indicate whether they have called on a specialised rating agency and, if so, must disclose the rating given. Moreover, any issuer can ask a bank for a commitment to provide financing should the market situation make it impossible to issue new notes once the current notes reach maturity. These backup lines came into their own in March 2020 when the Covid-19 crisis struck, as the commercial paper market virtually closed for a few weeks (before ECB provided liquidity by subscribing directly corporate commercial paper). Companies have to have such lines if they want their commercial paper issues to get an investment grade rating. Certain credit rating agencies, for example, will only keep their short-term rating of outstanding commercial paper at A1+ if 70% of the paper is covered by a backup line.
In addition to costing less than an overdraft, commercial paper gives the company some autonomy vis-à-vis its bankers. It is very flexible in terms of maturity and rates, but less so in terms of issue amounts.
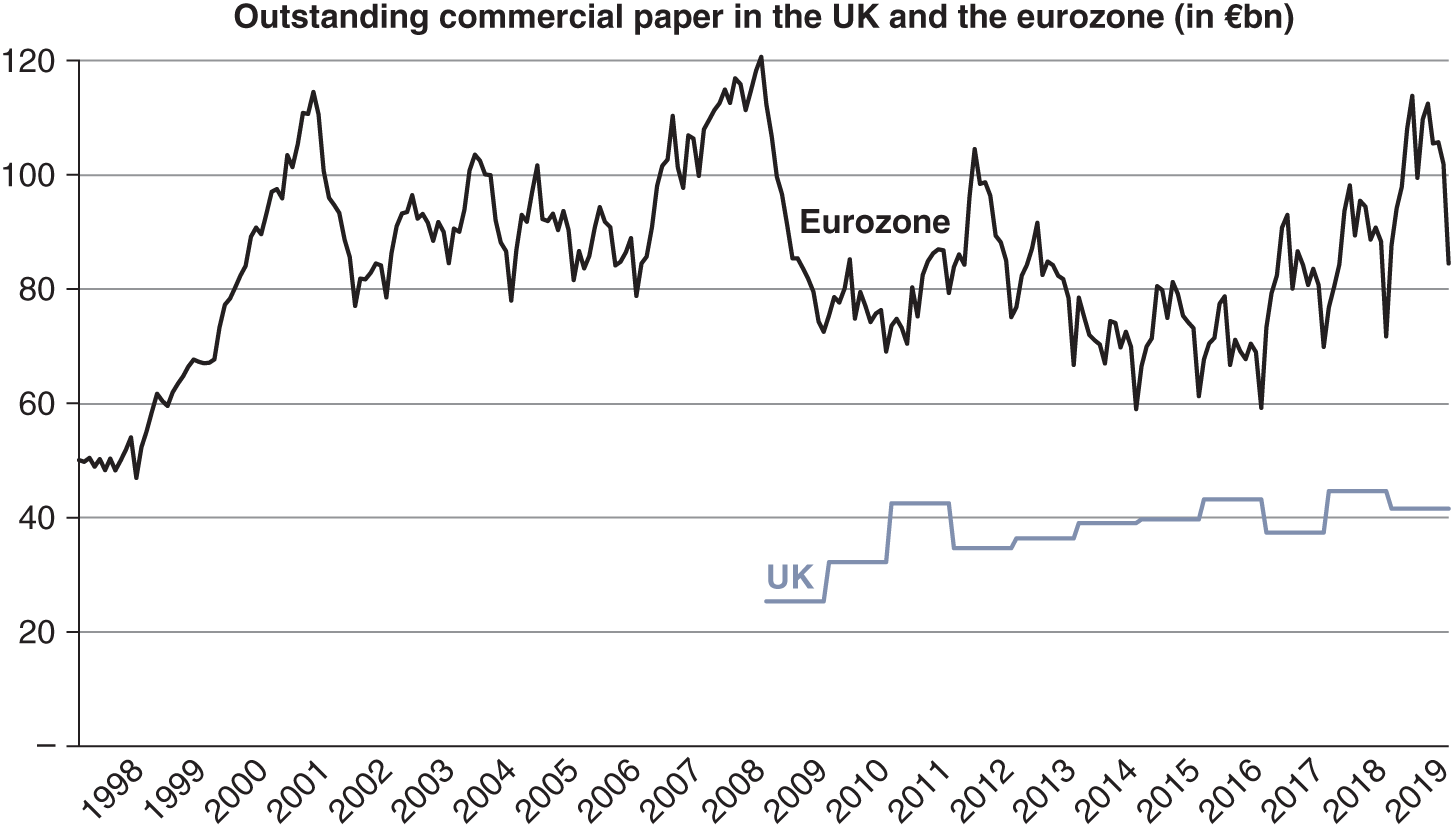
Source: Data from ECB
Regardless of their country of origin, companies can issue US commercial paper. Such issues are governed by Regulation 144A defining the terms and conditions of securities issues by foreign companies in the US (see Chapter 25).
2/ LONG-TERM MARKETABLE SECURITIES
These include two types. The first is bonds, which we have seen in the previous chapter; they are listed and potentially subscribed to by international investors. The second usually takes the form of bonds (listed or not) that are subscribed to through a private placement1 by a limited number of institutional investors (insurers, asset managers, pension funds) of a specific country.
There is a market for such products in the US, where there is a specific regulation for such issues, but also in Germany (Schuldschein), France (Euro PP) and in Belgium (mostly to individual investors).
Private placements have become a real alternative for the financing of large (ArcelorMittal, BASF, Rolls-Royce) or mid-sized (Vilmorin, Copenhagen Airport) or even smaller (Touax) groups. The transaction usually consists in the issue of a bond (sometimes a loan) in dollars or euros with a fixed rate. These financings generally have a long maturity (7 to 15 years, with the bulk of the issue with a 6- to 7-year maturity). Most investors keep their investment until maturity (buy and hold). As there is no liquidity constraint, the issues (or each tranche within an issue) can therefore be of reduced size (compared to a standard bond issue).
Private placements are appealing for groups that are willing to diversify their financing sources and have access to long-term financing without the need for a rating. The documentation can include some stringent covenants, and investors in such products may show much less flexibility than banks when it comes to renegotiation.
The increasing constraints on bank solvency have led to reduced loan offerings, in particular outside the domestic market. Financings outside the banking circuit have therefore developed (shadow banking), and the increasing success of private placements is just an illustration thereof.
Section 21.2 BANK DEBT PRODUCTS
Banks have developed a number of credit products that, contrary to market financing, are tailored to meet the specific needs of their clients.
Business loans (i.e. loans not linked to a specific asset, which we will see in the next section) have two key characteristics: they are based on interest rates and take into account the overall risk of the company.
The credit line will either be negotiated with a single bank, in which case the term bilateral loan is used, or with a number of banks (usually for larger amounts) and the firm will then put in place a club deal or a syndicated loan.
For companies, these loans are often a backup mechanism to meet any kind of cash payment.
Business loans are based on interest rates – in other words, cost, and the cheapest loan on offer usually wins the company’s business. They rarely come with ancillary services such as debt recovery, and are determined according to the maturity schedule and margin on the market rate.
These loans take into account corporate risk. The bank lending the funds agrees to take on the company’s overall risk as reflected in its financial health. A profitable company will always obtain financing as long as it adopts a sufficiently prudent capital structure. In fact, the financial loan is guaranteed by the corporate manager’s explicit compliance with a certain number of criteria, such as ratios, etc. If the loan is accompanied by a pricing or rating grid, the interest rate margin charged changes during the course of the credit in line with changes in the economic and financial situation of the company as measured by ratios or its rating. If it improves, the credit margin will fall; if it deteriorates, it will rise.
Financial brokers have started to develop their activities between SMEs and commercial banks by acting as intermediaries.
1/ TYPES OF BUSINESS LOANS
Overdrafts on current accounts are the corporate treasurer’s means of adjusting to temporary cash shortages but, given their high interest charges, they should not be used too frequently or for too long. Small enterprises can only obtain overdrafts against collateral, making the overdraft more of a secured loan.
Commercial loans are short-term loans that are easy to set up and therefore very popular.
The bank provides the funds for the period specified by the two parties. The interest rate is the bank’s refinancing rate plus a margin negotiated between the two parties. It generally ranges from 0.10% to 1.50% per year depending on the borrower’s creditworthiness, since there are no other guarantees.
Commercial loans can be made in foreign currencies either because the company needs foreign currencies or because the lending rates are more attractive.
Bridge loans are loans set up in anticipation of future revenues that will ensure their repayment: capital increase, bond issue, sale of a subsidiary, etc. Necessarily short-term, and often used for large amounts, it has evolved in parallel with financial transactions, particularly mergers and acquisitions. Its margin increases sharply over time (step ups) to encourage the borrower to refinance or dispose of planned assets.
Alternatively, the firm can put in place a revolving credit facility (RCF), which is a confirmed short-term or mid-term credit line. When the line is put in place, the firm will not have debt on its balance sheet, but it will have the capacity to draw on the credit line when it needs it. On the undrawn amount, the corporate will only pay a commitment fee. In addition to the spread, a utilisation fee will be added depending on the percentage of credit drawn.
If the firm has to finance a specific investment, it will put in place a term loan that will be less flexible than the RCF. Usually the borrower has the capacity to reimburse by anticipation, but will not be allowed to re-borrow any of the repaid amounts.
Note that loans can be extended to subsidiaries which can then borrow under the terms of the contract.
Syndicated loans are typically set up for facilities exceeding €50m which a single bank does not want to take on alone. The lead bank (or banks, depending on the amounts involved), known as the mandated lead arranger, will arrange the line and commit to undertake the full amount of the credit. It will then syndicate part of the loan to 5–20 banks, which will each lend part of the amount. The mandated lead arranger (known as the documentation agent) will receive an arrangement (or coordination) and underwriting fee and the other banks a lower participation fee (or flat fee).
Firm underwriting by one firm will allow the company to maintain maximum confidentiality with regard to the transaction, which could be crucial, for example in the case of the acquisition of a listed company. This can be achieved by having only one arranging bank that will bear the whole credit risk until the transaction becomes public (it can then syndicate the loan).
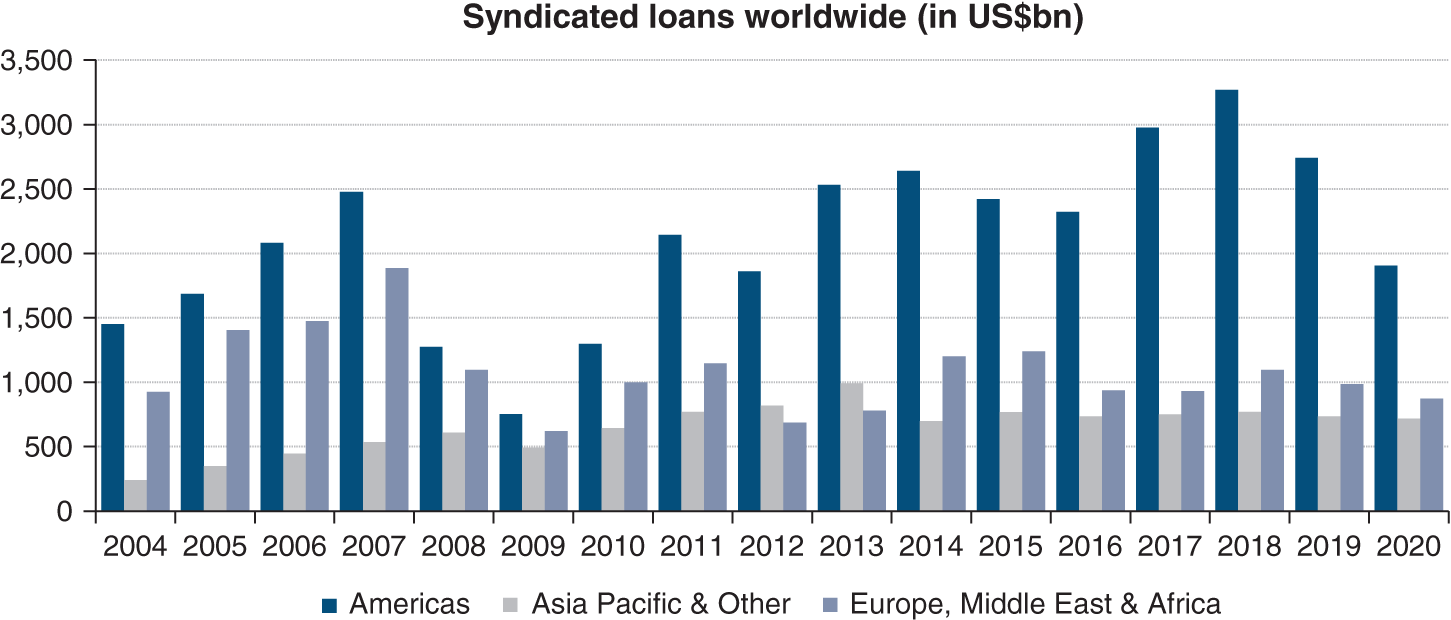
Source: Data from Thomson
When the loan is put in place with the house banks of the firm with no further syndication of the loan, we use the term club deal.
Much like the bond market, products promoting the environmental or societal virtues of the underlying company are emerging on the bank debt market. These are called impact loans. Certain large companies (Danone, Bel, Philips, etc.) have set up green RCFs (green loans) whose margin depends (marginally) on compliance with environmental objectives or criteria. Whilst the current financial impact for the company is marginal, this could change in an economic context of low liquidity markets, leading lenders to favour virtuous behaviour. In the short term, the corporate impact internally is predominantly psychological, but not necessarily negligible. Whereas €40bn had been lent in 2018, it was over €100bn in 2020.
2/ FEATURES OF THE LOAN DOCUMENTATION
The loan documentation sets out:
- the amount, maturity and purpose of the loan (i.e. the use of funds);
- the way the amount will be cashed in by the firm (one single payment, upon request by the firm, etc.), and minimum drawdown amounts;
- the interest rate, fixed or more often floating, periodicity of interest payments, rules for the computation of interest, fees to be paid;
- the reimbursement or amortisation profile;
- the potential early repayment options;
- the early termination events (change of control, …)
- the potential guarantees (by other group companies), pledges;
Banks include a certain number of covenants in the loan agreements, chiefly regarding accounting ratios, financial decisions and share ownership, which we will look at in detail in Section 39.2.
Two clauses are generally unavoidable:
- Pari passu clauses are covenants whereby the borrower agrees that the lender will benefit from any additional guarantees it may give on future credits.
- Cross default clauses specify that if the company defaults on another loan, the loan which has a cross default clause will become payable even if there is no breach of covenant or default of payment on this loan.
The agreement can also include a clause allowing banks to cancel the contract in the event of a material adverse change (MAC). The execution of such clauses (as well as “market disruption” clauses) is very complex from a legal point of view, but also from a commercial point of view.
Standardised legal documentation for syndicated loans has developed in Europe, led by the Loan Market Association (LMA) in London.
There exists a clear cyclicality on the loan market. After a period of high liquidity (2004–2007) marked by very favourable borrowing terms (both in terms of legal documentation and spreads), banks drastically tightened the terms and conditions of their loans after 2008 due to the weakening of their loan portfolios and the reduced market liquidity. Since 2013, lending conditions have become increasingly borrower-friendly and quite light.
Section 21.3 ASSET-BASED FINANCING
Unlike the previous financing tools which expose the lender to the company, the following financing tools only expose the lender to one of the company’s assets.
1/ FACTORING
Factoring is a credit transaction whereby a company holding an outstanding trade bill sells it to its bank or a specialised financial institution in exchange for the payment of the bill, less interest and commissions. Factoring companies or factors specialise in buying a given portion of a company’s trade receivables at a discount to the face value. The factoring company then collects the invoice payment directly from the debtors.
Factoring actually may include one or several of the following services to the firm:
- financing at an attractive interest rate;
- externalisation of receivables recovery;
- insurance against unpaid bills;
- off-balance-sheet financing.
Factoring is like discounting with additional services!
Banks increasingly offer non-recourse discounting services, which consist of an outright purchase of the trade receivables without recourse in the event of default. This technique removes contingent liabilities from the bank’s on- and off-balance-sheet accounts.
A factoring contract mentions:
- The scope of the contract (nature of the product, geography, type of debtors).
- The share of invoices available for financing (typically the bank will retain 8% to 15% of the invoices to cover the risk of unpaid invoices or litigation).
- The cap on financing and its features.
- The financing fee charged for the early availability of funds and that evolves in line with a money market index (EONIA, €ster of 3-month Euribor in Europe) plus a spread of up to 2.5%.
- The factoring fee that pays for the services and guarantee provided by the factor; this is computed as a percentage of invoices sold (between 0.2% and 2%). Its level depends on certain factors such as the nature and risk of clients, the statistics of unpaid invoices, the geographical spread of invoices, the average DSO (days sales outstanding), the number of customers and invoices and the average amount of invoices.
- Whether the contract allows for possible recourse to the company or not (if so, the firm will have a debt towards the factor after a pre-agreed period).
Large groups sometimes suggest that their suppliers put in place a reverse factoring line, whereby the supplier will get early payment of the invoice through a bank. The logic is the same as factoring, except that it is provided by the client. It is often used by clients in order to force lengthier payment terms (to the extent permitted by the applicable jurisdictions).
2/ DISCOUNTING
There are several short-term financing techniques that bridge the cash flow gap between invoicing and collection and are backed by the corresponding trade receivable. They are the counterpart to trade credit (inter-company credit), which is widely used in some countries (Continental Europe).
Discounting is a financing transaction whereby a company remits an unexpired commercial bill of exchange to the bank in return for an advance of the amount of the bill, less interest and fees.
The discounting bank becomes the owner of the bill and, ordinarily, is repaid when it presents the bill to its customer’s customer for payment. If, at maturity, the bill remains unpaid, then the bank turns to the company and asks them to pay. The company assumes the bankruptcy risk of its customer (such discounting is called discounting with recourse).
In principle, a company uses discounting to obtain financing based on the credit it extends to its own customers, which may be better known to the banking system than the company is. In this way, the company may be able to obtain better financing rates.
In discounting, the bank does not finance the company itself, but only certain receivables in its portfolio, i.e. the bills of exchange. For the bank, the risk is bound by a double guarantee: the credit quality of its customer backed by that of the issuer of the bill of exchange.
Under most accounting principles (including IFRS and US GAAP), discounted bills are reintegrated into accounts receivable and the bank advances are reported as debt.
For this reason, banks now also offer non-recourse discounting, which is a straight sale of customer receivables, under which the bank has no recourse to its customer if the bill remains unpaid at maturity. This technique allows the company to remove the receivables from its balance sheet and from its off-balance-sheet commitments and contingencies.
3/ INVENTORY FINANCING
Inventory financing is a form of pawn financing in which the firm retains ownership of inventory in which the lender has rights only in the event of the firm’s default.
All inventories are potentially concerned, except for those subject to retention of title and perishable inventories. The lender may request that the inventories securing its loan be physically transferred to the warehouses of a third party pledgor or isolated in a dedicated area (retention-of-title financing). Otherwise, they remain in the company. The financing is generally half of the net book value of the inventories concerned, bearing in mind that part of the company’s inventory is not concerned so as not to hinder its daily operations and logistics.
It is a preferred method of financing for financially weak companies to whom lenders would refuse to lend without this security.
Very old in certain sectors (agri-food, where it takes the form of a promissory note authorised by the company), inventory financing has a lower cost than an overdraft because it is well collaterised. However, it is cumbersome in terms of administrative procedures (contracts covering the financing, the pledges with a specialist collateral taker, audits, control and monitoring of the stock). The financing expires with the sale of the inventory and its exit is often through a discounting or factoring of the receivables from the buyers of the inventory. It is therefore a form of short-term financing with some exceptions (wine sector).
4/ FINANCIAL LEASES
While banks rarely offer long-term loans (more than five years) on the basis of a company’s intrinsic qualities alone, this is not the case for loans backed by a separate guarantee of the company’s assets through a suitable legal structure. Such an asset considerably limits the risk of insolvency and makes it possible to fix the price of the credit for a long period. Financial leasing enhances the value of the collateral provided by the borrower and is structured around this collateral.
Leasing is a contract for the lease of an asset over a fixed period of time between a company (industrial or commercial) and a bank or specialised institution that owns the asset, with a promise to sell (option to buy) the asset to the lessee at the end of the contract.
The interest of leasing for the “lender” is to have a loan secured by an asset legally distinct from the company’s assets. This technique can also be used in complex arrangements to play on the tax variable.
A company can thus use part of its operating fixed assets (land, buildings and other fixed assets) in a leasing system enabling it, if necessary, to buy back the asset at maturity for a contractually fixed value.
Two main types of leasing can be distinguished:
- equipment leasing concerns capital goods, machinery and tools. The company generally chooses its equipment from the supplier. It then goes to a leasing company which buys the goods from the supplier instead of the firm and leases them to the latter under an irrevocable commitment over a specified period. At the end of this period, the company has the option of renouncing the lease, renewing the contract, or acquiring the equipment for a price that takes into account the payments made during the lease period;
- real estate leasing concerns operations whereby a company leases real estate for professional use (offices, factories, hangars, etc.) owned by a leasing company with the possibility of becoming the owner of all or part of the leased property, at the latest at the end of the lease. Linked to the depreciation period of the leased asset, the duration of the real estate leasing contract is generally between 10 and 20 years.
The lessor and the lessee are bound by an agreement that sets out the conditions under which one of the parties may terminate its commitment.
While in the company’s financial statements leasing is often off-balance sheet since the company is not the legal owner of the asset, in the consolidated financial statements the economic reality prevails over the legal analysis. In the vast majority of cases, the asset is on the balance sheet and a corresponding debt is shown as a financial liability.
Finally, let us mention the long-term financial lease without purchase option (operating lease), which is widely used in certain sectors (IT, transport, etc.). This is a real lease of the property without the company having the option to acquire it after a certain period of use.2 This has nothing to do with leasing, where the initial intention of the borrower is ultimately to be able to acquire the asset financed in this way.
5/ SALE AND LEASE BACK
Sale and lease back is a procedure by which a company that owns a factory, an office block, a machine, etc. sells it to a leasing company or an investor, which immediately places it at the company’s disposal through an ordinary rental agreement or an equipment or real-estate leasing agreement, depending on the nature of the asset sold.
These transactions are described further in Chapter 52.
6/ SECURITISATION
Trade receivables or inventories are acquired by an SPV (special purpose vehicle) so as to pool risks and take advantage of the law of large numbers. The SPV finances itself by issuing securities to outside investors: equity, mezzanine debt, subordinated debt, senior debt, commercial paper, etc., so as to offer different risk–return profiles to investors. The SPV, such as a debt securitisation fund, receives principal payments emanating from the receivables it bought from the companies and uses the proceeds to cover its obligations on the securities it has issued.
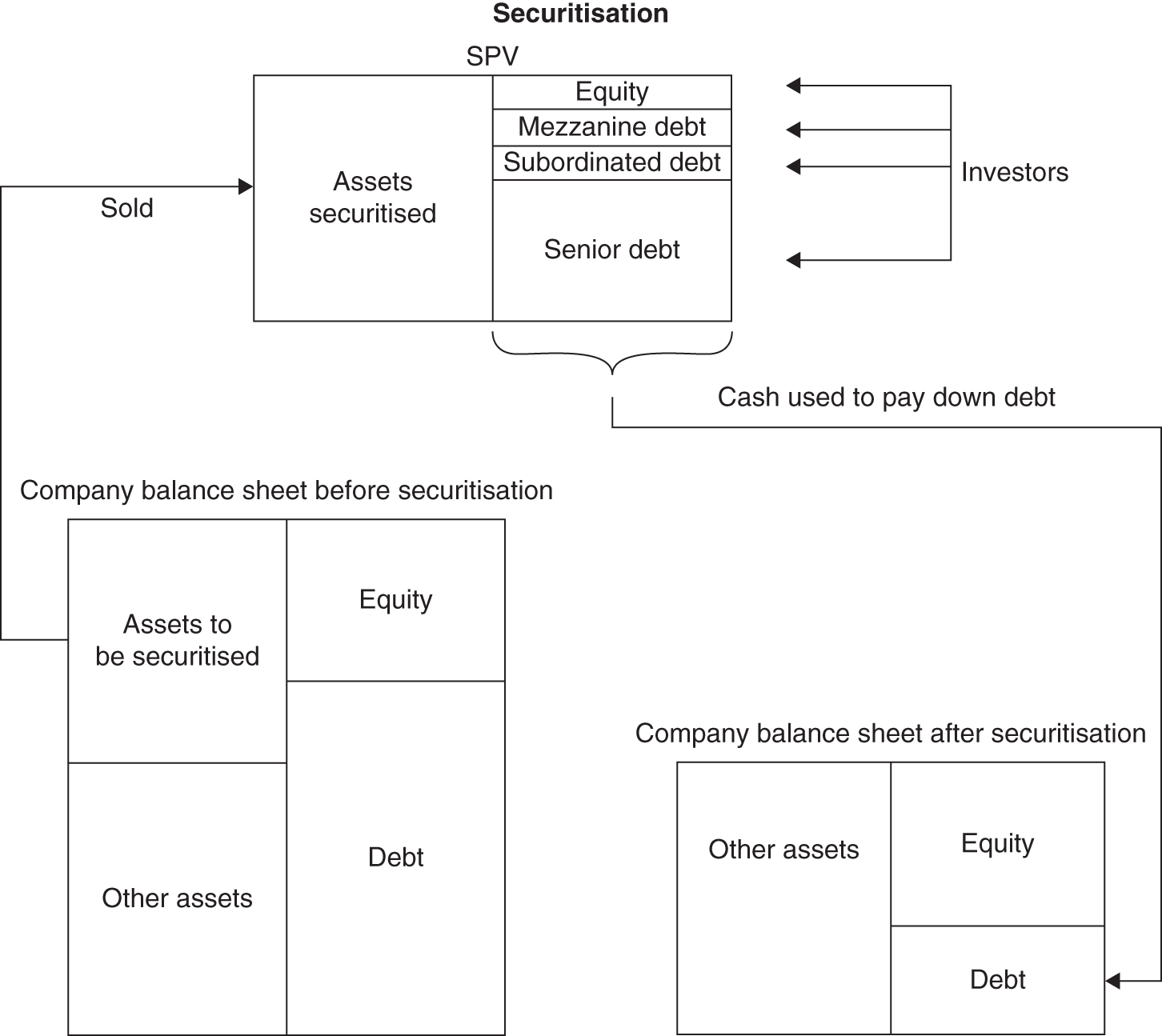
To boost the rating of the securities, the SPV buys more receivables or inventories than the volume of securities to be issued, the excess serving as enhancement. Alternatively, the SPV can take out an insurance policy with an insurance company. The SPV might also obtain a short-term line of credit to ensure the payment of interest in the event of a temporary interruption in the flow of interest and principal payments.
Once isolated, certain assets are of higher quality than the balance sheet as a whole, thus allowing the company to finance them at preferential rates. That said, the cost of these arrangements is higher than that of straight debt, especially for a high-quality borrower with an attractive cost of debt. Hence, they are hard to put in place for less than €50m, except if the platform is syndicated between several firms.
For example, ArcelorMittal securitises its account receivables and Avis its rental fleet, while Glencore does the same thing with its lead, nickel, zinc, copper and aluminium inventories.
The introduction before 2008 of subprime loans in some securitisation conduits to boost performance brought many of the securitisation vehicles and, in turn, the technique into disrepute. In Europe and in the USA, securitisation arrangers now have to retain 5% of the credit risk of securitised assets for their own account. This provides an incentive for them to take a close look at the quality of the assets and not to “wash their hands” of them once the deal is set up and distributed, to the detriment of the final investors and the credibility of the securitisation itself.
7/ BONDS AND GUARANTEES AND EXPORT CREDIT
Bonds and guarantees are not credit lines as the bank does not provide the funds unless the firm defaults (in which case the bank will pay instead of the firm). They are off-balance-sheet commitments.
For the firm, a bank guarantee generally allows it to defer payment or not to provide a down payment (rents, customer advance payment).
Bid bonds are issued by the bank of a company that responds to a call for tenders to ensure that it will honour its business commitments if it is selected. Performance bonds are issued by a bank to guarantee the proper performance of a contract (construction, etc.) within a certain timeframe. Finally, warranty bonds are issued from the commissioning of an installation to cover any defects found after delivery. They are used in the real-estate sector or for capital goods (construction of factories or power plants).
A corporate can ask a bank to issue a financial guarantee or letter of credit to secure a payment (representation and warranties, litigation). They also make it possible to obtain loans from another bank or other body more easily or on better terms, or to conclude a contract which, without the guarantee provided by the guarantor, could not have been envisaged.
The documentary credit ensures the successful completion and settlement of a commercial contract, most often between an exporter and an importer of different nationalities. The banks of the two trading partners guarantee their respective customers, which limits the risk of unpaid delivery or goods paid for but not delivered.
After signing the commercial contract between an importing buyer and an exporting seller, it is up to the buyer to initiate the issuance of the documentary credit by contacting its bank (issuing bank), which passes on to a correspondent bank the opening of a documentary credit payable on its coffers against the presentation of a list of documents predefined by the buyer. The seller will have the assurance of being paid when the bank has received and recognised the required documents as being in conformity.
There are several types of payment procedures (at sight, by deferred payment, by negotiation or discount or by acceptance of a draft), but their basis remains the same: to establish a relationship of trust between business partners who do not know each other.
The documentary credit is a method of payment, of guaranteeing payment, but also often facilitates financing (because it allows discounting), the precise terms of which are defined by the “Rules and Practices” of the International Chamber of Commerce (ICC).
The stand-by letter of credit (SBLC) is subject to the same operating rules as the documentary credit, defined by the “Rules and Practices” issued by the ICC. It is used to cover a current flow of transactions between a client and its supplier for an outstanding amount up to the limits predefined in the letter of credit.
Buyer’s credit or export credit is used to finance export contracts of goods and/or services between an exporter and the buyer importing the goods/services. The banks granting the buyer’s credit undertake to provide the borrower with the funds needed to pay the supplier directly according to the terms specified by the contract.
The borrower, in turn, gives the bank an irrevocable mandate to pay the funds only to the supplier. The agreement stipulates the interest rates, duration and repayment conditions of the loan, and any bank fees or penalties that may arise if the borrower fails to meet its obligations.
The credit agreement also specifies that the transaction is purely financial, since the borrower must repay the funds notwithstanding any disputes that may arise in the course of its business with the exporter. The advantages to the supplier are:
- insurance against payment default;
- the cost of the credit is not deducted from the contract while the risk level remains acceptable to the bank;
- the portion of the contract that must be paid upon maturity is not on the balance sheet.
The credit risk taken by the bank setting up a buyer credit is partially covered by export credit agency under certain conditions of duration, rates, etc., which have been accepted by the signatory states of the “consensus” agreements (OECD countries). These agreements specify the rules for financing export contracts for capital goods and/or services benefiting from official support in order to neutralise the financing criterion in the evaluation of commercial offers. In addition to the guarantee of an export credit agency, official support applies to the terms of export financing, in particular the duration and rate of credit, which makes it very attractive compared to market financing.
Certain types of buyer’s credit can also be used to finance major projects and thus resemble project financing, which we will discuss now.
8/ PROJECT FINANCING
Bankers’ imaginations know no bounds when creating specialised bank financing packages that combine funding with accounting, tax, legal or financial advantages. Sometimes lenders take the global risk of the group in the form of subordinated debts (see Chapter 24). In other cases they may only be taking the risk of one project of the group, which, most of the time, is isolated into a separate entity.
(a) Principle and techniques
Project financing is used to raise funds for large-scale projects with costs running into the hundreds of millions of euros, such as oil extraction, mining, oil refineries, the purchase of methane tankers, the construction of power plants or bridges, etc.
Lenders base their decision to extend such financing on an assessment of the project itself rather than the borrower, and on the projected cash flows generated by the project that will repay the credit. They rely on the project’s assets as collateral for the debt.
This type of financing was first used in the early 1930s by American banks to extend financing to oil prospectors who could not offer the guarantees required for standard loans. The banks drew up loan contracts in which a fraction of the oil still in the ground was given as collateral and part of the future sales were set aside to repay the loan.
With this financial innovation, bankers moved beyond their traditional sphere of financing to become more involved, albeit with a number of precautions, in the actual risk arising from the project.
But it is all too easy to become intoxicated by the sophistication and magnitude of such financial structures and their potential returns. Remember that the bank is taking on far more risk than with a conventional loan, and could well find itself at the head of a fleet of super oil tankers of uncertain market value. Lastly, the parent company cannot completely wash its hands of the financial risk inherent in the project, and banks will try to get the parent company’s financial guarantee, just in case.
When considering project financing, it is essential to look closely at the professional expertise and reputation of the contractor. The project’s returns, and thus its ability to repay the loan, often depend on the contractor’s ability to control a frequently long and complex construction process in which cost overruns and missed deadlines are far from rare. Project financing is not just a matter of applying a standard technique. Each individual project must be analysed in detail to determine the optimal financing structure so that the project can be completed under the best possible financial conditions.
The financiers, the future manager of the project and the contractor(s) are grouped in a pool taking the form of a company set up specifically for the project. This company is the vehicle for the bank financing.
Clearly, project financing cannot be applied to new technologies which have uncertain operating cash flows, since the loan repayment depends on these cash flows. Similarly, the operator must have acknowledged expertise in operating the project, and the project’s political environment must be stable to ensure that operations proceed smoothly. Only thus can investors and banks be assured that the loan will be repaid as planned.
In addition to investors and banks, two other players can take on an important role in project finance:
- international financial organisations such as the World Bank and regional development banks like the EBRD,3 especially if the project is located in a developing country. These institutions may lend funds directly or guarantee the loans extended by the other banks;
- export-facilitating organisations like Bpifrance in France, Hermès in Germany or SACE in Italy, which underwrite both the financial and the commercial risks arising on the project.
(b) Risks and how they are hedged
The risks on large projects arise during three quite distinct stages:
- when the project is being set up;
- during construction;
- during operations.
Risks arise as soon as the project is in the planning stage. Analysing a major project can take up to several years and requires considerable expertise and numerous technical and financial feasibility studies. All this can be quite costly. At this stage, no one is sure that the project will actually materialise. Moreover, when there is a call for tenders, the potential investors are not even sure that their bid will be retained.
But, of course, the greatest risk occurs during construction, since any loss can only be recouped once the facilities are up and running!
Some of the main risks incurred during the construction phase are:
- Cost overruns or delays. These are par for the course on large projects that are complex and lengthy. Such risks can be covered by specific insurance that can make up for the lack of income subject to the payment of additional premiums. Any claims benefits are paid directly to the lenders of the funds, or to both borrowers and lenders. Another method is for the contractor to undertake to cover all or part of any cost overruns and to pay an indemnity in the event of delayed delivery. In exchange, the contractor may be paid a premium for early completion.
- Non-completion of work, which is covered by performance bonds and contract guarantees, which unconditionally guarantee that the industrial unit will be built on schedule and with the required output capacity and production quality.
- “Economic upheavals” imposed by the government (e.g. car factories in Indonesia, dams in Nigeria, with initial strong support by local governments, which was withdrawn later on because of cash shortages or a change of government) and arbitrary acts of government, such as changes in regulations.
- Natural catastrophes that are not normally covered by conventional insurance policies.
As a result, the financing is released according to expert assessments of the progress made on the project.
Risk exposure culminates between the end of construction and the start of operations. At this point, all funds have been released but the activity that will generate the flows to repay them has not yet begun and its future is still uncertain. Moreover, a new risk emerges when the installations are delivered to the client, since they must be shown to comply with the contract and the client’s specifications. Because of the risk that the client may refuse to accept the installations, the contract usually provides for an independent arbitrator, generally a specialised international firm, to verify that the work delivered is in conformity with the contract.
Once the plant has come on stream, anticipated returns may be affected by:
- Operating risks per se: faulty design of the facilities, rising operating or procurement costs. When this occurs, the profit and loss account diverges from the business plan presented to creditors to convince them to extend financing. Lenders can hedge against this risk by requiring long-term sales contracts, such as:
- take or pay: these contracts link the owner of the facilities (typically for the extraction and/or transformation of energy products) and the future users whose need for it is more or less urgent. The users agree to pay a certain amount that will cover both interest and principal payments, irrespective of whether the product is delivered and of any cases of force majeure;
- take and pay: this clause is far less restrictive than take or pay, since clients simply agree to take delivery of the products or to use the installations if they have been delivered and are in perfect operating condition.
- Market risks. These risks may arise when the market proves smaller than expected, the product becomes obsolete or the conditions in which it is marketed change. They can be contained, although never completely eliminated, by careful study of the sales contracts, in particular the revision and cancellation clauses which are the linchpin of project financing, as well as detailed market research.
- Foreign exchange risks are usually eliminated by denominating the loan in the same currency as the flows arising on the project or through swap contracts (see Chapter 51).
- Abandonment risk arises when the interests of the industrial manager and the bankers diverge. For example, the former may want to bail out as soon as the return on capital employed appears insufficient, while the latter will only reach this conclusion when cash flow turns negative. Here again, the project financing contract must lay down clear rules on how decisions affecting the future of the project are to be taken.
- Political risks, for which no guarantees exist but which can be partly underwritten by state agencies.
Section 21.4 OTHER DEBT PRODUCTS
Since mid-2010, regulatory relaxations and new technologies have enabled the emergence of debt financing that involves neither banks nor markets.
Crowdlending allows companies, predominantly SMEs, to contract debt in the form of bonds from individuals on specialised Internet platforms such as October. Amounts per issuer range from a few tens of thousands of euros to €8m per 12-month period.
Some investment funds have specialised in granting loans directly to companies to finance them globally or some of their assets.
SUMMARY
QUESTIONS
ANSWERS
BIBLIOGRAPHY
NOTES
- 1 See Section 25.6.
- 2 See Section 7.12 for the accounting and financial treatments of operating leases.
- 3 European Bank for Reconstruction and Development.
Chapter 22. SHARES
Chapter 22
SHARES
One of a kind, or one of many?
As we saw in Chapter 4, the capital that is injected or left in the business by investors, which is exposed to the various risks of commercial or industrial ventures, and for which in return they receive the profits of, is called equity.
A share or a stock is a security that is not redeemed – the investment can only be realised through a disposal – and whose revenue flows are uncertain. It is in compensation for these two disadvantages that shareholders have a say in managing the company via the voting rights attached to their shares.
The purpose of this chapter is to present the key parameters used in analysing stocks and show how the stock market operates. For a discussion of stock as a claim option on operating assets, refer to Chapter 34, and to find out more about stock as a claim on assets and commitments, see Chapter 31 on company valuation.
Section 22.1 BASIC CONCEPTS
This section presents the basic concepts for analysing the value of stocks, whether or not they are listed. Remember that past or future financial transactions could artificially skew the market value of a stock with no change in total equity value. When this happens, technical adjustments are necessary, as explained in Section 22.5 of this chapter. We will then assume that they have been done.
1/ VOTING RIGHTS
Shares are normally issued with one voting right each. For our purposes, this is more of a compensation for the risk assumed by the shareholder than a basic characteristic of stock.
A company can issue shares with either limited or no voting rights. These are known under different names, such as preference shares, savings shares or simply non-voting shares.
At the other extreme, companies in some countries, such as the US and Sweden, issue several types of shares (“A” shares, “B” shares, etc.) having different numbers of voting rights. Some shareholders use this to strengthen their hold on a company, as we will see in Chapter 41.
2/ EARNINGS PER SHARE (EPS)
EPS is equal to net attributable profit divided by the total number of shares issued. EPS reflects the theoretical value creation during a given year, as net profit belongs to shareholders.
There is no absolute rule for presenting EPS. However, financial analysts generally base it on earnings restated from non-recurring items, as shown below:
ArcelorMittal’s 2021 EPS was estimated in mid-2021 to be $4.99 (it was −$0.64 in 2020).
Some companies have outstanding equity-linked securities, such as convertible bonds, warrants and stock options. In this case, in addition to standard EPS, analysts calculate fully diluted EPS. We will show how they do this in Section 22.5.
3/ DIVIDEND PER SHARE (DPS)
Dividends are generally paid out from the net earnings for a given year, but can be paid out of earnings that have been retained from previous years. Companies sometimes pay out a quarterly (in the USA) or half-year (in the UK) dividend.
In 2021 ArcelorMittal paid a $0.30 dividend on 2020 results (it did not pay a dividend in 2020 on its 2019 results).
Some shares – like preference shares – pay out higher dividends than other shares or have priority in dividend payments over those other shares. They are generally non-voting shares.
4/ DIVIDEND YIELD
Dividend yield per share is the ratio of the last dividend paid out to the current share price:
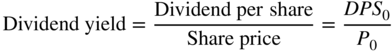
The dividend yield on ArcelorMittal is 1% (dividend of $0.30 on a share with a price of $26.4).
The average yield on stocks listed on European stock markets is currently about 3%.
DIVIDEND YIELD – PAN-EUROPEAN SECTORS (AS OF 1 JANUARY)
| Years | Automotive | Biotechnology | Chemistry | Defence | Financial Institutions | Food | Oil & Gas | Real Estate | Telecom | Utilities |
|---|---|---|---|---|---|---|---|---|---|---|
| 1990 | 2.4% | 1.1% | 4.0% | 6.6% | 2.7% | 3.1% | 4.6% | 3.3% | 4.4% | 4.7% |
| 1995 | 0.8% | 0.4% | 3.1% | 0.3% | 3.1% | 3.5% | 4.0% | 4.7% | 4.1% | 4.3% |
| 2000 | 2.4% | 0.1% | 2.6% | 2.7% | 2.1% | 2.7% | 2.5% | 2.8% | 1.0% | 2.8% |
| 2005 | 2.5% | 0.5% | 2.4% | 2.5% | 2.7% | 1.9% | 2.5% | 2.9% | 1.9% | 3.1% |
| 2010 | 1.1% | 0.5% | 3.9% | 2.8% | 3.1% | 2.4% | 4.6% | 3.5% | 5.8% | 5.6% |
| 2015 | 2.2% | 0.6% | 3.6% | 2.4% | 3.3% | 2.7% | 5.3% | 2.9% | 4.1% | 5.1% |
| 2016 | 2.2% | 0.5% | 3.6% | 2.3% | 3.8% | 2.7% | 5.8% | 2.7% | 4.3% | 4.8% |
| 2017 | 2.4% | 0.6% | 3.1% | 2.1% | 3.9% | 2.9% | 4.7% | 3.0% | 4.7% | 4.8% |
| 2018 | 2.5% | 0.5% | 2.8% | 1.7% | 3.4% | 2.5% | 4.5% | 2.8% | 4.3% | 4.4% |
| 2019 | 3.6% | 0.6% | 4.6% | 2.0% | 4.6% | 2.8% | 4.9% | 2.7% | 5.0% | 4.3% |
| 2020 | 3.3% | 0.4% | 4.1% | 1.6% | 4.2% | 2.2% | 4.9% | 2.4% | 5.1% | 3.7% |
| 2021 | 2.3% | 0.5% | 3.6% | 1.2% | 3.2% | 2.6% | 6.7% | 2.4% | 4.4% | 3.2% |
Source: Factset, Datastream
5/ PAYOUT RATIO
The payout ratio is the percentage of earnings from a given year that is distributed to shareholders in the form of dividends. It is calculated by dividing dividends by earnings for the given year:
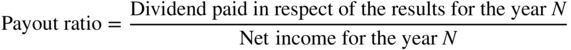
When the payout ratio is above 100%, a company is distributing more than its earnings; it is tapping its reserves. Conversely, a payout close to 0% indicates that the company is reinvesting almost all its earnings into the business. In 2018, European companies paid out an average of about 45% of their earnings.
It will be clear that the higher the payout ratio, the weaker future earnings growth will be. The reason for this is that the company will then have less funds to invest. As a result, fast-growing companies such as SolarWorld and Google pay out little or none of their earnings, while a mature company would pay out a higher percentage of its earnings. Mature companies are said to have moved from the status of a growth stock to that of an income stock (also called a yield stock), i.e. a company that pays out in dividends a large part of its net income, such as a utility.
The dividend is legally drawn on parent company profits. However, it should be assessed on the basis of consolidated net attributable profit – the only meaningful figure, as in most cases the parent company is merely a holding company.
2021 ArcelorMittal’s payout ratio is not relevant as the company will pay a dividend whereas it was loss making (EPS of –$1.20) in 2020.
6/ BOOK VALUE OF EQUITY (OR NET ASSET VALUE) PER SHARE
Book value of equity per share is the accounting estimate of the value of a share. While book value may appear to be directly comparable to equity value, it is determined on an entirely different basis – it is the result of strategies undertaken up to the date of the analysis and corresponds to the amount invested by the shareholders in the company (i.e. new shares issued and retained earnings).
Book value may or may not be restated. This is generally done only for financial institutions and holding companies.
7/ COST OF EQUITY (EXPECTED RATE OF RETURN)
According to the CAPM (see Chapter 19), the cost of equity is equal to the risk-free rate plus a risk premium that reflects the stock’s market (or systematic) risk.
8/ SHAREHOLDER RETURN (HISTORICAL RATE OF RETURN)
In a given year, shareholders receive a return in the form of dividends (dividend yield) and the increase in price or market value (capital gain):
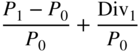
Total shareholder return (TSR) is calculated in the same way, but over a longer period. It reflects the IRR of the investment in the stock.
9/ LIQUIDITY
A listed security is said to be liquid when it is possible to buy or sell a large number of shares on the market without it having too great an influence on the price. Liquidity is a typical measure of the relevance of a share price. It would not make much sense to analyse the price of a stock that is traded only once a week, for example.
A share’s liquidity is measured mainly in terms of free float, trade volumes and analyst coverage (number of analysts following the stock, quality and frequency of brokers’ notes).
(a) Free float
The free float is the proportion of shares available to purely financial investors, to buy when the price looks low and sell when it looks high. Free float does not include shares that are kept for other reasons, i.e. control, sentimental attachment or “buy and hold” strategies.
Loyalty is (unfortunately) not a financial concept and a skyrocketing share price could make sellers out of loyal shareholders, thus widening the free float.
Free float can be measured either in millions of euros or in percentage of total shares.
(b) Volumes
Liquidity is also measured in terms of volumes traded daily. Here again, absolute value is the measure of liquidity, as a major institutional investor will first try to determine how long it will take to buy (or sell) the amount it has targeted. But volumes must also be expressed in terms of percentage of the total number of shares and even as a percentage of free float. Liquidity is generally considered good when more than 0.2% of the free float is traded each day.
10/ MARKET CAPITALISATION
Market capitalisation is the market value of company equity. It is obtained by multiplying the total number of shares outstanding (number of shares issued less the number of treasury shares1, see Section 7.19) by the share price.
However, rarely can the majority of shares be bought at this price at the same time, for example, in an attempt to take control and appoint new management. Most often, a premium must be paid (see Chapters 31 and 45).
It is a mistake to take only the shares in free float in determining market capitalisation. All shares must be included, as market cap is the market value of company equity and not of the free float.
By way of illustration, you will find in the appendix to this book the top twenty market capitalisations of the world’s major economies.
On 6 May 2021, ArcelorMittal had a market cap of $34,920m.
Section 22.2 MULTIPLES
In order to understand the level of stock prices, investors must make some comparisons with comparable investments (similar stocks). By doing so, they can arbitrage between stocks, taking into account their belief about the companies’ qualities and the level of their prices. To achieve this objective, investors normally relate the stock price to a financial item.
There are two basic categories of multiples:
- those which allow for a direct estimate of the market capitalisation. In this section, we will refer specifically to the price to earnings ratio (P/E);
- those which are independent of the capital structure of the company. These multiples allow for the estimate of the value of the entire firm (firm or enterprise value) or, similarly, the market value of the capital employed. The EBIT multiple (EV/EBIT) and the EBITDA multiple (EV/EBITDA) will be presented in this section. Since capital employed is financed by equity and net debt, the enterprise value must then be allocated between creditors (first) and shareholders. The following formula shows how to derive the value of equity from the enterprise value:
1/ EBITDA AND EBIT MULTIPLES
(a) The principle
Investors interested in estimating the enterprise value of a company frequently find that the stock market believes that a fair value for similar companies could be, for example, eight times their EBIT (or operating profit). With a pinch of salt, the investor can then decide to apply the same multiple to the EBIT of the company they are considering.
Investors name this ratio the EBIT multiple:
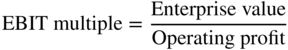
If the operating profit remains unchanged, and disregarding corporate income taxes and discounting, these figures imply that investors must wait eight years before they can recover their investment. Conversely, if the operating profit increases, they will not have to wait so long.
In practice, when applying the multiple, financial analysts prefer using the operating profit of the current period or of the next period.
Where the comparison is made using companies with significant different corporate income tax rates (because they belong to different countries, for example), it is more appropriate to consider an operating profit net of taxes (net operating profit after tax, or NOPAT). This result can easily be obtained by multiplying the operating profit by (1 – the observed corporate tax rate). This is rarely done.
Similarly, EBITDA multiple can be computed as:
(b) The multiple drivers
Although the EBITDA/EBIT multiples are ratios that summarise a lot of information, their value is basically determined by three factors: the growth rate of the operating profit, the risk of capital employed and the level of interest rates.
- The growth rate of the operating profit. There is a certain degree of correlation between the multiple and the expected growth of the operating profit. This is no surprise. Investors will be more willing to pay a higher price if the operating profit is expected to grow at a high rate (as long as the firm creates value, i.e. the investments generate a sufficient return). They are now buying with a high EBITDA/EBIT multiple based on current EBITDA or operating profit but with a more reasonable EBITDA/EBIT multiple based on future EBITDA or operating profit that is expected to be much higher.
The reverse is also true: investors will not be ready to pay a high EBITDA/EBIT multiple for a company, the EBITDA or operating profit of which is expected to remain stable or increase slowly. Hence the low multiples for companies with low growth prospects.
The reader should also not forget that behind the growth of the EBITDA/operating profit is the growth of both revenues and EBITDA/operating margins.
The following graph shows the relation between the medium-term growth rate of the operating profit of some European companies and their multiples.
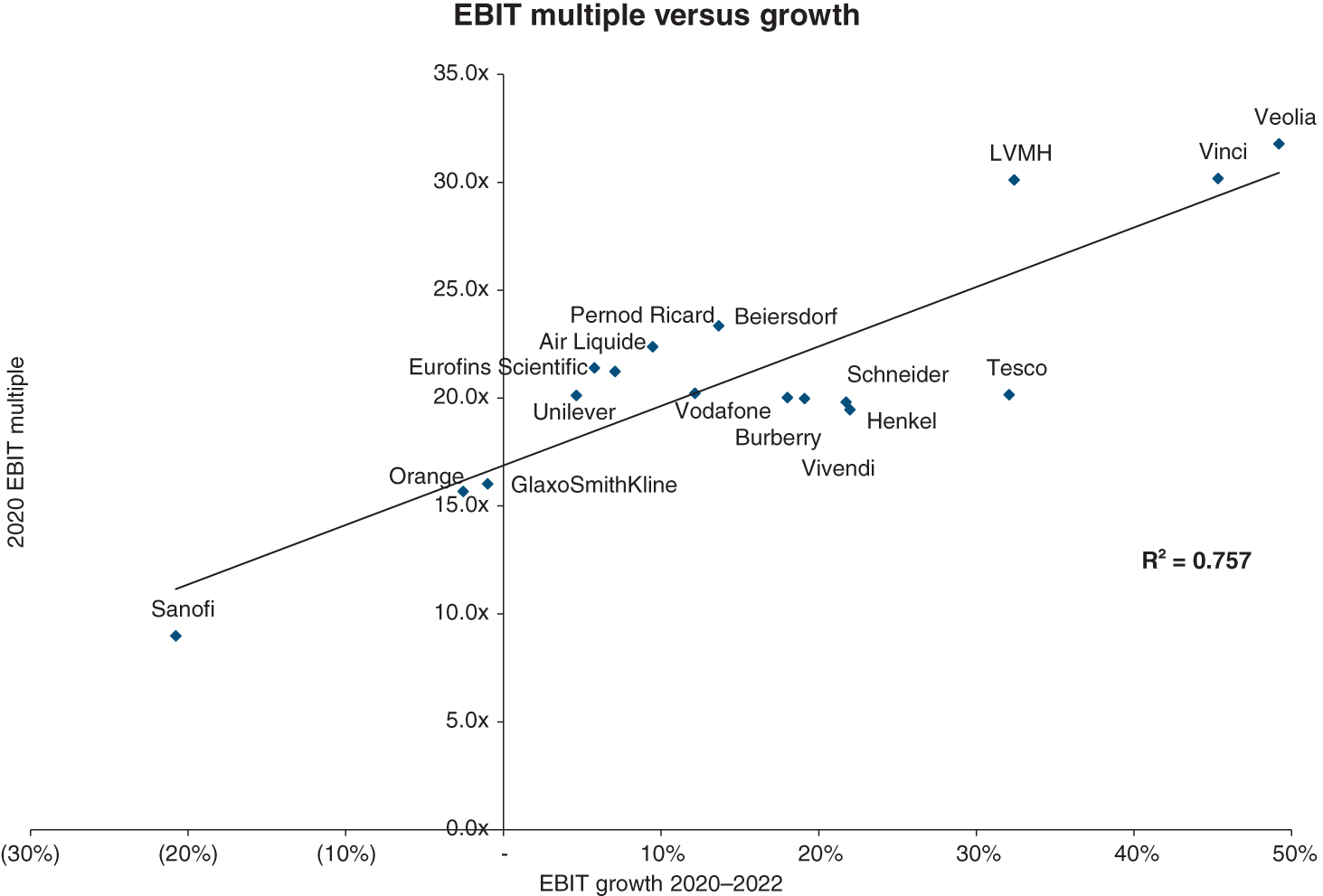
Source: Data from Exane BNP Paribas
- The risk of the capital employed. The link between growth rate and multiples is not always verified in the market. Sometimes some companies show a low multiple and a high growth rate, and vice versa.
This apparent anomaly can often be explained by considering the risk profile of the company. Analysts and investors in fact do not take the expected growth rate for granted. Thus, they tend to counterweight the effects of the growth rate with the robustness of these estimates.
- The level of interest rates. There is a strong inverse correlation between the level of interest rates and the EBITDA and EBIT multiples. This link is rather intuitive: our reader is, in fact, perfectly aware that high interest rates increase the returns expected by investors (think, for example, about the CAPM equation!), thus reducing the value of any asset.
Generally speaking, we can say that the level of the multiple can be frequently explained – at a specific moment – by the current level of interest rates in the economy.
The EBITDA and EBIT multiples allow us to assess the company valuation compared to the overall market.
2/ PRICE TO EARNINGS (P/E)
(a) The principle
Even if the EBITDA and EBIT multiples have become very popular in the investor and analyst community, a ratio simpler to compute has been used for a while to determine share prices. The P/E (price/earnings ratio), which, when multiplied by the earnings per share (EPS), provides an estimate for the value of the share.
P/E is equal to:
Another way to put this is to consider the aggregate values:
EPS reflects theoretical value creation over a period of one year. Unlike a dividend, EPS is not a revenue stream.
As an illustration, the following table shows the P/E ratios of the main markets since 1990. We can see the impact of the 2000 bubble on P/Es for technology, media, and telecommunications groups but also the impact of shifts in the automobile industry (electric, autonomous cars) in 2019.
While there is no obligation to do so, P/E is based on estimated earnings for the current year. However, forward earnings are also considered; for example, P/EN +1 expresses the current market value of the stock divided by the estimated earnings for the following year. For fast-growing companies or companies that are currently losing money, P/EN +1 or P/EN +2 are sometimes used, either to give a more representative figure (and thus avoid scaring the investor!) or because, in the case of loss-making companies, it is impossible to calculate P/E for year N.
The widespread use of P/E (which is implicitly assumed to be constant over time) to determine equity value has given rise to the myth of EPS as a financial criterion to assess a company’s financial strategy. Such a decision might or might not be taken on the basis of its positive or negative impact on EPS. This is why P/E is so important, but it also has its limits, as we will demonstrate in Chapters 26, 27 and in Section IV.
HISTORICAL P/E RATIOS – PAN-EUROPEAN SECTORS (AS OF 1 JANUARY)
| Years | Automotive | Biotechnology | Chemistry | Defence | Financial Institutions | Food | Oil & Gas | Real Estate | Telecom | Utilities |
|---|---|---|---|---|---|---|---|---|---|---|
| 1990 | 6.7 | 21.7 | 8.3 | 6.9 | 16.1 | 14.1 | 11.2 | 24.8 | 12.8 | 11.1 |
| 1995 | 13.4 | 30.4 | 13.5 | 14.3 | 14.1 | 12.9 | 17.3 | 20.4 | 12.7 | 13.4 |
| 2000 | 13.2 | 180.5 | 18.4 | 19.0 | 19.3 | 17.1 | 38.5 | 21.2 | 51.7 | 17.3 |
| 2005 | 12.6 | 25.6 | 24.9 | 32.6 | 15.8 | 17.8 | 15.4 | 19.6 | 20.5 | 13.9 |
| 2010 | 52.5 | 19.0 | 20.4 | 10.4 | 13.8 | 11.8 | 18.4 | 13.0 | 12.3 | 11.2 |
| 2015 | 8.6 | 25.0 | 14.9 | 17.2 | 13.4 | 22.3 | 11.0 | 17.1 | 17.0 | 13.6 |
| 2016 | 9.7 | 40.3 | 13.4 | 17.1 | 11.9 | 16.3 | 16.8 | 17.8 | 20.2 | 14.0 |
| 2017 | 9.3 | 31.5 | 19.0 | 19.7 | 12.5 | 24.2 | 25.1 | 17.1 | 13.5 | 13.7 |
| 2018 | 9.0 | 42.5 | 17.9 | 27.3 | 12.8 | 25.5 | 21.7 | 18.2 | 15.5 | 13.4 |
| 2019 | 6.2 | 22.8 | 10.0 | 21.5 | 10.1 | 18.9 | 11.8 | 13.9 | 15.3 | 13.8 |
| 2020 | 8.9 | 37.4 | 8.1 | 21.4 | 11.6 | 27.2 | 15.9 | 19.6 | 17.5 | 13.2 |
| 2021 | 22.8 | 42.4 | 22.5 | 24.1 | 11.8 | 19.8 | 85.4 | 21.0 | 15.0 | 20.5 |
Source: Data from Factset, Datastream
P/E is conceptually similar to the EBIT multiple, and even more so to the NOPAT multiple. The latter is a division of enterprise value by after-tax operating profit, while P/E is a division of market value of equity by net profit.
Hence, many of the things we have said about the EBIT multiple also apply to P/E:
- Another way of understanding P/E is to note that it expresses market value on the basis of the number of years of earnings that are being bought. Thus, an equity value of 100 and earnings of 12.5 means the P/E is 8. This means that if EPS remains constant, the investor will have to wait eight years to recover their investment, while omitting corporate income taxes and discounting. If the EPS rises (falls), the investor will have to wait less (more) than eight years.
- In an efficient market, the greater the EPS growth, the higher the P/E and vice versa (on condition that the firm creates value, i.e. has a higher ROE than the rate of return required by shareholders).
- The greater the perceived risk, the lower the P/E and vice versa.
- P/E is inversely proportional to interest rates: all other factors being equal, the higher the interest rates, the lower the P/Es and vice versa, again assuming efficient markets.
P/E is used in the same way as the EBITDA or EBIT multiple. To value a company, it is useful to set it alongside other companies that are as comparable as possible in terms of activity, growth prospects and risk, and then apply their P/E to it.
P/E reflects a risk that the EBIT multiple does not – financial structure – which comes on top of the risk presented by the operating assets.
(b) P/E and investors’ required rate of return
Inverse P/E, also called earnings yield, is sometimes mistakenly used in approximating investors’ required rate of return. This should only be done in those very rare cases where earnings growth is nil and the company pays out 100% of its earnings. Here is our reasoning:
Then:
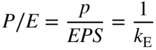
and thus:
The P/E of a company with an EPS of 12 that is trading at 240 would then be:
The inverse P/E is just 5%, whereas the required return nowadays is probably about 8%.
All in all, the inverse P/E reflects only an immediate accounting return for a new shareholder who has bought the share for V and who has a claim on EPS:
- A very low return means that shareholders expect EPS growth to be strong enough to ultimately obtain a return commensurate with their required rate of return.
- A very high rate means that immediate return is uncertain and shareholders expect negative EPS growth to ultimately bring accounting return closer to their required rate of return.
- A normal rate, i.e. in line with the required rate of return, means that EPS growth is expected to be nil, and the investment is considered a perpetual annuity.
3/ OTHER MULTIPLES
Apart from the EBIT multiple and the P/E, investors and analysts sometimes use the following multiples.
(a) Sales multiple
Sometimes the value of the firm is assessed in proportion to its sales, and the ratio enterprise value/sales is then computed. This ratio is often used to derive the value of shops or very small companies. For example, a rule of thumb holds that within the food industry, businesses are worth twice the amount of their sales, whereas a telecoms company is worth three times its sales.
Using such multiples implies that the compared firms have the same type of margin. It implies somehow a normative return over sales for firms in a certain sector.
We believe that sales multiples should not be used for mid-sized or large companies as they completely disregard profitability. They have often been used in the past, in times of bull markets, to value emerging technology, for example, as such companies did not show a positive EBIT!
The same type of criticism can be levelled against multiples of numbers of subscribers, numbers of clicks, etc., or other multiples of volume of activity. These multiples not only assume a comparable return over sales but also the same revenue per unit.
(b) Free cash flow multiple
The ratio of enterprise value to free cash flow, or EV/FCF, is a concept similar to the multiple of operating income mutatis mutandis. It represents the number of times free cash flow is capitalised by the enterprise value.
This ratio should be a much better indicator than the EBIT multiple, whose accounting nature of the denominator makes it susceptible to manipulation. Indeed, free cash flow is the cash flow that the firm can redistribute to its fund providers, shareholders and lenders, after financing its investments. However, it is of little significance for companies with weak or negative cash flows because they are in a strong growth phase or at the bottom of the cycle.
In other words, this ratio only makes sense for mature groups whose investments are stable, making free cash flow very significant. The inverse of this ratio is called free cash flow yield.
(c) Price to book ratio (PBR)
The PBR (price to book ratio) measures the ratio between market value and book value:
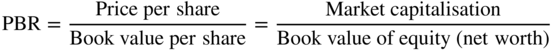
The PBR can be calculated either on a per share basis or for an entire company. Either way, the result is the same.
It may seem surprising to compare book value to market value, which, as we have seen, results from a company’s future cash flow. Even in the event of liquidation, equity value can be below book value (due, for example, to restructuring costs, accounting issues, etc.).
However, there is an economic link between book value and market value, as long as book value correctly reflects the market value of assets and liabilities.
It is not hard to show that a stock’s PBR will be above 1 if its market value is above book value, when the ROE is above the required rate of return (kE). The reason for this is that if a company consistently achieves 15% ROE, and the shareholders require only 10%, then a book value of 100 would mean an equity value of 150, and the shareholders will have achieved their required rate of return:
However, the PBR will be below 1 if the ROE is below the required rate of return (kE).
Theoretically, a sector cannot show equity value below book value for long, as sector consolidation will soon intervene and re-establish a balance, assuming that markets are efficient. Nor can a sector have equity value higher than book value for long, as new entrants will be attracted to the sector and bring down the abnormally high returns. Market equilibrium will sooner or later have been re-established.
As an illustration, here are the PBRs seen on the main European markets since 1990:
PBR – PAN-EUROPEAN SECTORS (AS OF 1 JANUARY)
| Years | Automotive | Biotechnology | Chemistry | Defence | Financial Institutions | Food | Oil & Gas | Real Estate | Telecom | Utilities |
|---|---|---|---|---|---|---|---|---|---|---|
| 1990 | 1.2 | nm* | 1.5 | 0.9 | 1.5 | 1.8 | 1.7 | 1.2 | 1.5 | 1.3 |
| 1995 | 1.2 | nm* | 1.5 | 1.3 | 1.1 | 1.7 | 1.9 | 1.0 | 1.7 | 1.5 |
| 2000 | 1.8 | 5.4 | 2.2 | 2.2 | 2.0 | 1.8 | 2.6 | 0.9 | 4.2 | 2.2 |
| 2005 | 1.1 | 3.8 | 1.7 | 1.7 | 1.8 | 3.9 | 2.9 | 1.3 | 3.0 | 2.2 |
| 2010 | 0.9 | 3.4 | 2.0 | 1.6 | 1.1 | 3.5 | 1.8 | 1.0 | 2.3 | 1.6 |
| 2015 | 1.2 | 5.2 | 2.1 | 2.7 | 1.0 | 3.7 | 1.0 | 1.2 | 2.4 | 1.2 |
| 2016 | 1.2 | 6.7 | 2.0 | 3.6 | 1.0 | 3.7 | 1.0 | 1.3 | 2.6 | 1.3 |
| 2017 | 1.1 | 6.2 | 2.4 | 3.8 | 0.9 | 3.7 | 1.3 | 1.1 | 2.3 | 1.4 |
| 2018 | 1.2 | 5.3 | 2.6 | 3.9 | 1.1 | 4.0 | 1.4 | 1.3 | 2.6 | 1.5 |
| 2019 | 0.9 | 4.1 | 1.6 | 3.9 | 0.9 | 3.7 | 1.3 | 1.1 | 2.3 | 1.5 |
| 2020 | 0.9 | 5.1 | 1.6 | 5.6 | 1.0 | 5.0 | 1.2 | 1.3 | 2.3 | 1.8 |
| 2021 | 1.1 | 5.8 | 2.0 | 5.6 | 0.9 | 5.1 | 1.1 | 1.3 | 2.0 | 2.2 |
* nm = not meaningful
Source: Data from Factset, Datastream
Section 22.3 KEY MARKET DATA
We are now able to fill in the blanks of the chart below, but it will only make sense if you have first assessed the company’s strategy and finances.
We have filled in the data for ArcelorMittal, whose free float is significant (c. $18bn) and is covered by 20 analysts.
ArcelorMittal’s share price is highly dependent on changes in raw material prices, in particular steel and iron ore, the price of which has decreased significantly between 2014 and 2016, and again between 2018 and 2019 as a result of trade tensions between China and the United States. As a result, ArcelorMittal’s share price was halved between end 2014 and end 2015, before being multiplied by 3.5 since its low of February 2016, following which it then crashed by 50% from its highs of early 2018 and was again multiplied by 3 from a low point in May 2020. This is a cyclical investment!
In 2018, the payment of a symbolic dividend started again, after having stopped in 2016, given its negative free cash flows. Payment of dividend was again suspended in 2020 and resumed in 2021.
As we noticed earlier, ArcelorMittal does not create value, its ROE (9.4% in 2018) being negative below the return required by shareholders (c. 12% given the risk). Its market capitalisation is therefore below the book value of equity (even if lowered in 2015 by exceptional impairment).
Liquidity is very high, with over 1% of capital exchanged on average every day.
KEY MARKET DATA ON ARCELORMITTAL
| Past | Current | Future | |||
|---|---|---|---|---|---|
| In $ | 2019 | 2020 | 2021 | 2022 | 2023 |
| Adjusted share price | |||||
| High | 24.24 | 19.25 | 26.37 | ||
| Low | 12.53 | 6.46 | 17.58 | ||
| Average or last | 17.54 | 19.16 | 26.37 | ||
| Absolute data | |||||
| Number of fully diluted shares (m) | 1,021 | 1,080 | 1,080 | ||
| Market capitalisation (m) | 17,908 | 20,693 | 28,480 | ||
| Equity, group share (m) | 38,521 | 38,280 | 43,885 | 46,054 | 48,165 |
| Value of net debt (m) | 19,997 | 14,000 | 11,437 | ||
| Enterprise value (m) | 39,999 | 40,690 | 42,480 | ||
| Multiples | |||||
| Fully diluted EPS | –2.40 | –0.68 | 5.10 | 3.51 | 3.07 |
| EPS growth | n.s. | n.s. | n.s. | –31% | –13% |
| P/E | n.s. | n.s. | 5.2 | 7.5 | 8.6 |
| Operating profit (m) | 1,202 | 451 | 8,334 | 5,664 | 4,872 |
| EBIT multiple | 35.3 | n.s. | 5.1 | 7.5 | 8.7 |
| Price/book ratio (PBV) | 0.5 | 0.5 | 0.5 | ||
| Dividend | |||||
| Dividend per share (DPS) | 0.30 | 0.00 | 0.30 | 0.43 | 0.47 |
| DPS growth | n.s. | n.s. | n.s. | 43% | 9% |
| Net yield | 1.7% | 0.0% | 1.1% | ||
| Payout | –12% | n.s. | 6% | 12% | 15% |
| Return | |||||
| Beta (β) | 1.9 | 2.4 | 2.1 | ||
| Risk premium: rM – rF | 6.8% | 10.3% | 8% | ||
| Risk-free rate: rF | –0.4% | –0.5% | –0.5% | ||
| Required rate of return: kE | 12.5% | 24.2% | 16.3% | ||
| Return on equity: rE | –6.4% | –1.9% | 12.6% | ||
| Actual return (capital gains and dividends) | –15% | 9% | 39% | ||
| Liquidity | |||||
| Free float | 62.4% | 64.4% | 64.4% | ||
| Share of capital traded daily | 0.55% | 0.54% | 0.62% | ||
| Number of analysts covering the stock | 24 | 21 | 20 | ||
Section 22.4 HOW TO PERFORM A STOCK MARKET ANALYSIS
In order to perform a stock market analysis, we advise readers to follow the following battle plan tailored by Marc Vermeulen:

Readers who are not new to corporate finance are advised to follow on from this chapter by reading Chapter 31, which is the logical continuation of this chapter.
Section 22.5 ADJUSTING PER SHARE DATA FOR TECHNICAL FACTORS
1/ REWRITE HISTORY, IF NECESSARY
“Let’s not mix apples with oranges.” This old saying applies to the adjustment of per share data after the detachment of rights and for free share awards and rights issues which, from a technical point of view, can modify the value of a stock.
(a) Free share awards
Suppose a company decides to double its equity by incorporating its reserves, and issues one new share for each existing share. Each shareholder is then the owner of twice as many shares without having paid additional funds and with no change to the company’s financial structure. The unit value of the shares has simply been divided into two.
Naturally, the company’s equity value will not change, as two shares will be equal to one previously existing share. However, the share price before and after the operation will have to be adjusted to obtain a comparable series.
In this case, simply divide the shares existing after the free share award by two. The adjustment coefficient is 1/2.
More generally, if new shares are issued for N already existing shares, then the adjustment coefficient is as follows:
(b) A rights issue with an exercise price below the current share price
This is the second reason we might have to adjust past per share data. We will go further into detail in Chapter 25, which deals with share offerings.
To subscribe to the new shares, investors must first buy one or more preemptive subscription rights detached from previously existing shares, whose price is theoretically such that it doesn’t matter whether they buy previous existing shares or use the rights to buy new ones. The detachment of the right from the existing shares makes an adjustment necessary.
For a rights issue, the adjustment coefficient is:
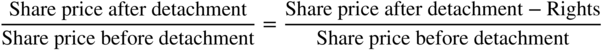
If P is the price of the already existing share, E the issue price of the new shares, the number of new shares and N the number of already existing shares, then the adjustment coefficient will be equal to:
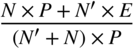
To make the adjustment, simply multiply all the share data (e.g. price, EPS, DPS, BV/S) before the detachment by this coefficient.
As you have seen, the adjustment consists in rewriting past stock performance to make it comparable to today and tomorrow, and not the reverse.
2/ THE IMPACT OF FUTURE TRANSACTIONS
When equity-linked securities (convertible bonds, mandatory convertibles, bonds with warrants attached, stock options, etc.) have been issued, financial managers must factor these potential new shares into their per share data. Here again, we must adjust in order to obtain an average number of outstanding shares.
As there is at least potential dilution, we have to assume full conversion in calculating the per share data (EPS, BV/S, etc.) on a fully diluted basis. This is easy to do for convertible bonds (CBs). Simply assume that the CBs have been converted. This increases the number of shares but lowers financing costs, as interest is no longer paid on the CBs.
For warrants (or stock options), two methods can be used. The first method, called the treasury method, is commonly used: it assumes investors will exercise their in-the-money2 warrants and the company will buy back its own shares with the proceeds. The company thus offsets some of the dilution caused by the exercise of the warrants. This is the method recommended by the IASB.
The following example will illustrate the method: on 1 September 2016, Loch Lomond Corporation decided to issue 100,000 equity warrants exercisable from 1 January 2019 to 1 January 2023 at one share at €240 per warrant.
In 2021, EPS is €10m (net income 2021) divided by 1,000,000 (number of shares), i.e. €10.
As of 31 December 2021, Loch Lomond’s share price is €300, all the warrants are in the money and thus are assumed exercised: 100,000 new shares are issued. The exercise of the warrants raises the following sum for the company: 100,000 × €240 = €24,000,000.
The company could use this money to buy back 80,000 of its own shares trading at €300. Fully diluted EPS can be computed as follows:
Note that only in-the-money diluting securities are restated; out-of-the-money securities are not taken into account.
The second method, called the investment of funds method, assumes that all investors will exercise their warrants and that the company will place the proceeds in a financial investment. Let’s go back to that last example and use this method.
In this method, we assume all warrants are exercised by investors and the proceeds are invested at 0.2% after taxes pending use in the company’s industrial projects. Fully diluted EPS would be as follows:
As can be seen, the two methods produce different results as a direct consequence of the different uses of the cash proceeding from the exercise of warrants.
The treasury method can be considered to be the closest to the financial markets, as the main figure it uses is the company’s share price. However, the treasury method assumes that the best investment for a company is to buy back its own shares.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTES
Chapter 23. OPTIONS
Chapter 23
OPTIONS
The haunted house, or how to pay for being frightened!
Options are more complex than shares or bonds. Moreover, in their daily use they have more to do with financial management than finance. However, we will see that many financial products (warrants, stock options) can be analysed as options or as the combination of an option and a less risky asset. Have some fun by discovering the options hidden in any financial product!
A convertible bond can be seen as a combination of a conventional bond and an option. An undrawn revolving credit facility can be analysed as an option on a loan.
We will also examine how options theory can be applied to major financial strategy decisions within a company.
The purpose of this chapter is not to make you a wizard in manipulating options or to teach you the techniques of speculation or hedging with options, but merely to show you how they work in practice.
Section 23.1 DEFINITION AND THEORETICAL FOUNDATION OF OPTIONS
1/ SOME BASIC DEFINITIONS
There are call (buy) options and put (sell) options. The asset that can thereby be bought or sold is called the underlying asset. This can be either a financial asset (stock, bond, Treasury bond, forward contract, currency, stock index, etc.) or a physical one (a raw material or mining asset, for example).
The price at which the underlying asset can be bought or sold is called the strike price. The holder of an option may exercise it (i.e. buy the underlying asset if they hold a call option or sell it if they hold a put option) either at a given date (exercise date) or at any time during a period called the exercise period, depending on the type of option held.
A distinction is made between US-style options (the holder can exercise their right at any moment during the exercise period) and European-style options (the holder can only exercise their right on the exercise date). Most listed options are US-style options, and they are found on both sides of the Atlantic, whereas most over-the-counter (OTC) options are European-style.
Here are two examples:
Let’s say Peter sells Helmut a call option on the car manufacturer BMW having an €85 strike price and maturing in nine months. For nine months (US-style option) or after nine months (European-style option), Helmut will have the right to buy one BMW share at a price of €85, regardless of BMW’s share price at that moment. Helmut is not required to buy a share of BMW from Peter, but if Helmut wants to, Peter must sell him one for €85.
Obviously, Helmut will exercise his option only if BMW’s share price is above €85. Otherwise, if he wants to buy a BMW share, he will simply buy it on the market for less than €85.
Now let’s say that Paul buys from Clara put options on \$1m in currency at an exchange rate of €1.1/\$, exercisable six months from now. Paul may in six months’ time (if it’s a European-style option) sell \$1m to Clara at €1.1/\$, regardless of the dollar’s exchange rate at that moment. Paul is not required to sell dollars to Clara but, if he wants to, Clara must buy them from him at the agreed price.
Obviously, Paul will only exercise his option if the dollar is trading below €1.1.
The above examples highlight the fundamentally asymmetric character of an option. An option contract does not grant the same rights or obligations to each side. The buyer of any option has the right but not the obligation, whereas the seller of any option is obliged to follow through if the buyer requests.
The value at which an option is bought or sold is sometimes called the premium. It is obviously paid by the buyer to the seller, who thereby obtains some financial compensation for a situation in which they have all the obligations and no rights.
Hence, a more precise definition of an option would be:
When the option matures, we can show the payouts for the buyer and the seller of the call option in the following way:
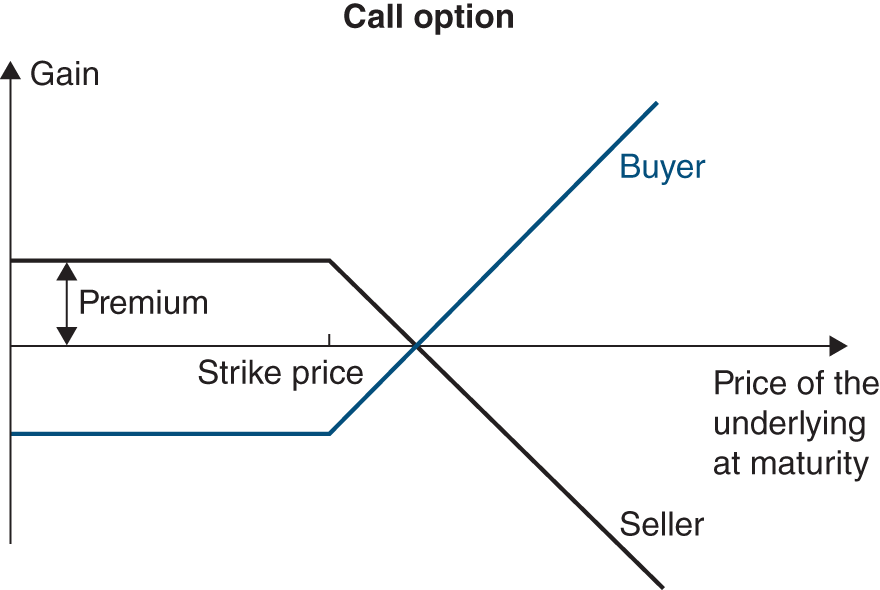
At maturity, if BMW is trading at €90, Helmut will exercise his option and buy his BMW share at €85. He can then sell it again if he wishes, and make €5 in profit (minus the premium he paid for the option).
Similarly, for the put option:
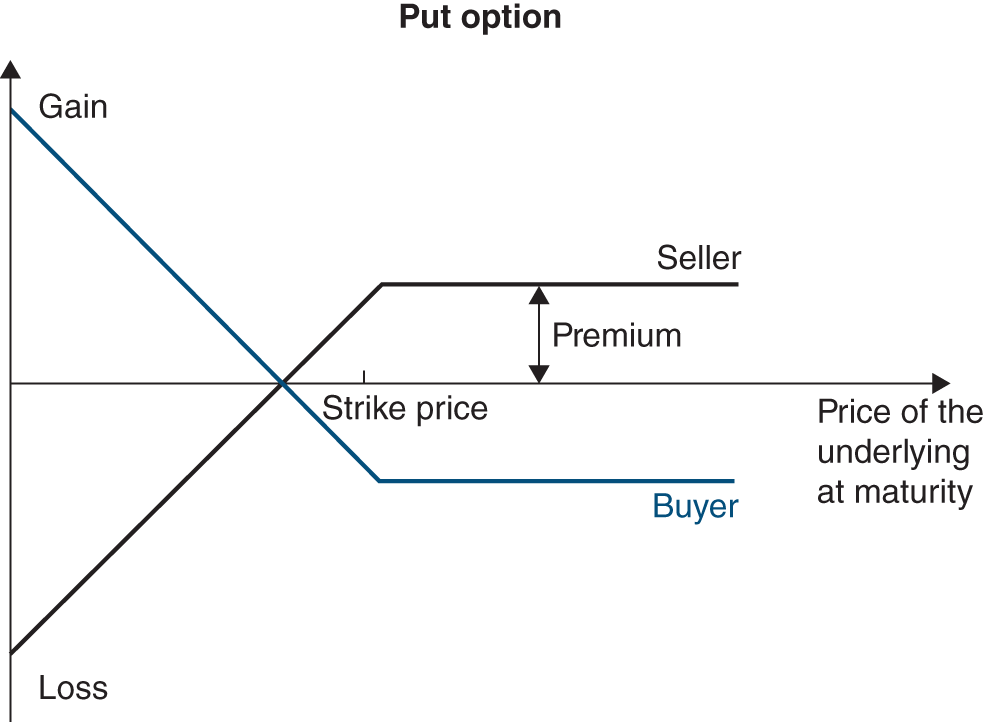
This diagram highlights the asymmetry of risk involved: the buyer of the option risks only the premium paid, while his potential profit is almost unlimited, while the seller’s gain is limited to the value of the premium received, but his loss is potentially unlimited.
2/ THE THEORETICAL BASIS OF OPTIONS
In a risk-free environment, if we knew today with certainty what would happen tomorrow, options would have no interest.
If the future were known with certainty there would be no risk and all financial assets would bring in the same return, i.e. the risk-free rate. What purpose would an option have, i.e. the right to buy or sell, if we already knew what the price would be at maturity? What purpose would a call option on Siemens serve, at a strike price of €170, if we already knew that Siemens’ share price would be below €160 at maturity and that the option would therefore not be exercised? And if we knew that, at maturity, Siemens’ share price would be €250, the price of the option would be such that it would offer the risk-free rate, just like Siemens’ shares, since the future would be known with certainty.
Options might therefore be called pure financial products, as they are merely remuneration of risk. There is no other basis to the value of an option.
Section 23.2 MECHANISMS USED IN PRICING OPTIONS
Let’s suppose that Felipe buys a call option on Diageo at a £30 strike price, maturing in nine months, and simultaneously sells a put option on the same stock at a £30 strike maturing in nine months. Assuming the funds paid for the call option are largely offset by the funds received for the sale of the put option, what will happen at maturity?
If Diageo is trading at above £30, Felipe will exercise his call option and pay £30. The put option will not be exercised, as his counterparty will prefer to sell Diageo at the market price.
If at maturity Diageo is trading below £30, Felipe will not exercise his call option, but the put option that he sold will be exercised and Felipe will have to buy Diageo at £30.
Hence, regardless of the price of the underlying asset, buying a call option and selling a put option on the same underlying asset, at the same maturity and at the same strike price, is the same thing as a forward purchase of the underlying asset at maturity at the strike price.
In other words:
Assuming fairly valued markets, we can thus deduce that at the end of the exercise period:
It looks like this on a chart:
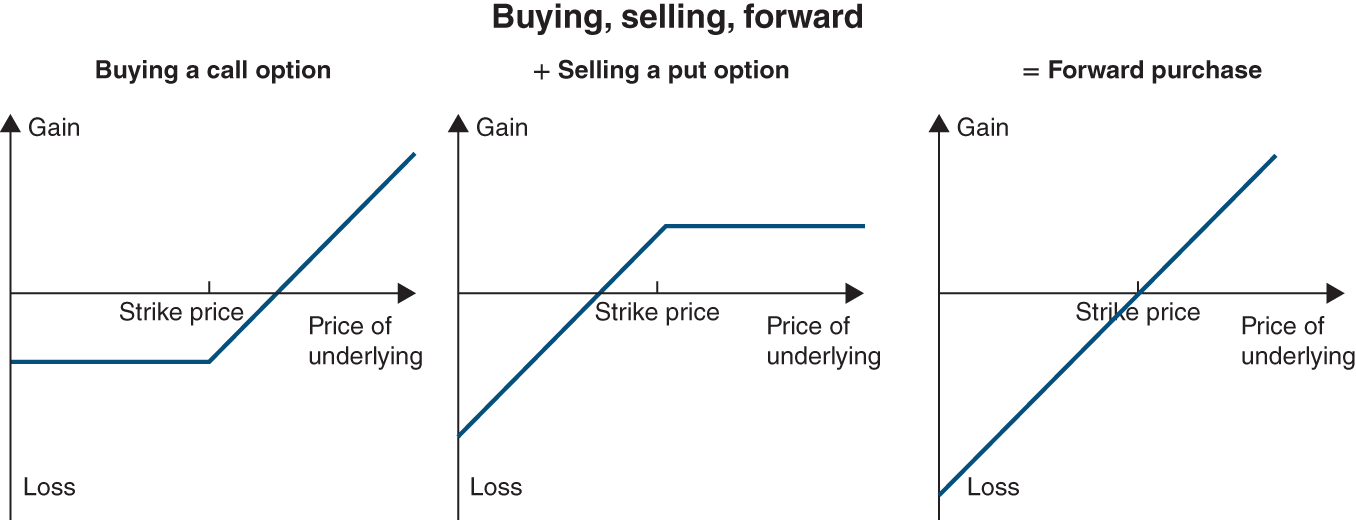
We can see that the profit (or loss) of this combination is indeed equal to the difference between the price of the underlying asset at maturity and the strike price.
Let’s now consider the following transaction: Evgueni wants to buy Diageo stock, but does not have the funds necessary at his immediate disposal. However, he will be receiving £30 in nine months, enough to make the purchase. He can thus borrow the present value of £30, nine months out, and buy Diageo.
At maturity, the profit (or loss) on this transaction will thus be equal to the difference between the value of the Diageo shares and the repayment of the £30 loan.
So we are back to the previous case and can thus affirm that in value terms:
This equation shows that we can “manufacture” a synthetic call option based on a put option and vice versa, as long as we can buy and sell the underlying asset and place or borrow funds.
We have used a stock for the underlying asset, but the above statement applies to any underlying asset (currencies, bonds, raw materials, etc.).
Section 23.3 ANALYSING OPTIONS
1/ INTRINSIC VALUE
Intrinsic value is the difference (if it is positive) between the price of the underlying asset and the call option’s strike price. For a put option, it’s the opposite. The intrinsic value of a put option is the difference, if positive, between the exercise price of the put option and the price of the underlying asset. And if the difference is not positive, then the intrinsic value is null. In the rest of this chapter, unless otherwise mentioned, we will use call options as examples.
By definition, intrinsic value is never negative.
Let’s take a call option on sterling, with a strike price of €1.15/£ and maturing at end-December. Let’s say that it is now June and that the pound is trading at €1.26.
What is the option’s value? The holder of the option may buy a pound for €1.15, while the pound is currently at €1.26.
This immediate possible gain is none other than the option’s intrinsic value, which will be billed by the seller of the option to the buyer. The option will be worth at least €0.11.
Technically, a call option is said to be:
- out of the money when the price of the underlying asset is below the strike price (zero intrinsic value);
- at the money when the price of the underlying asset is equal to the strike price (zero intrinsic value);
- in the money when the price of the underlying asset is above the strike price (positive intrinsic value).
The reader will have understood that a put option is said to be:
- out of the money when the price of the underlying asset is above the strike price (zero intrinsic value);
- at the money when the price of the underlying asset is equal to the strike price (zero intrinsic value);
- in the money when the price of the underlying asset is below the strike price (positive intrinsic value).
2/ TIME VALUE
Now let’s say we are in October, sterling is trading at €1.04. The option would be out of the money (€1.04 is less than the €1.15 strike price) and the holder would not exercise it. Does this mean that the option is worthless? No, because there is still a chance, however slight, that sterling will move over €1.15 by the end of December. This would make the option worth exercising. So the option has some value, even though it is not worth exercising right now. This is called time value.
For an in-the-money call option, i.e. whose strike price (€1.15) is below the value of the underlying asset (let’s now assume that £1 = €1.27), intrinsic value is €0.12. But this intrinsic value is not all of the option’s value. Indeed, we have to add time value, which ultimately is just the anticipation that intrinsic value will be higher than it is currently. For there is always a probability that the price of the underlying asset will rise, thus making it more worthwhile to wait to exercise the option.
In more concrete terms, time value represents “everything that could happen” from now until the option matures.
Hence:
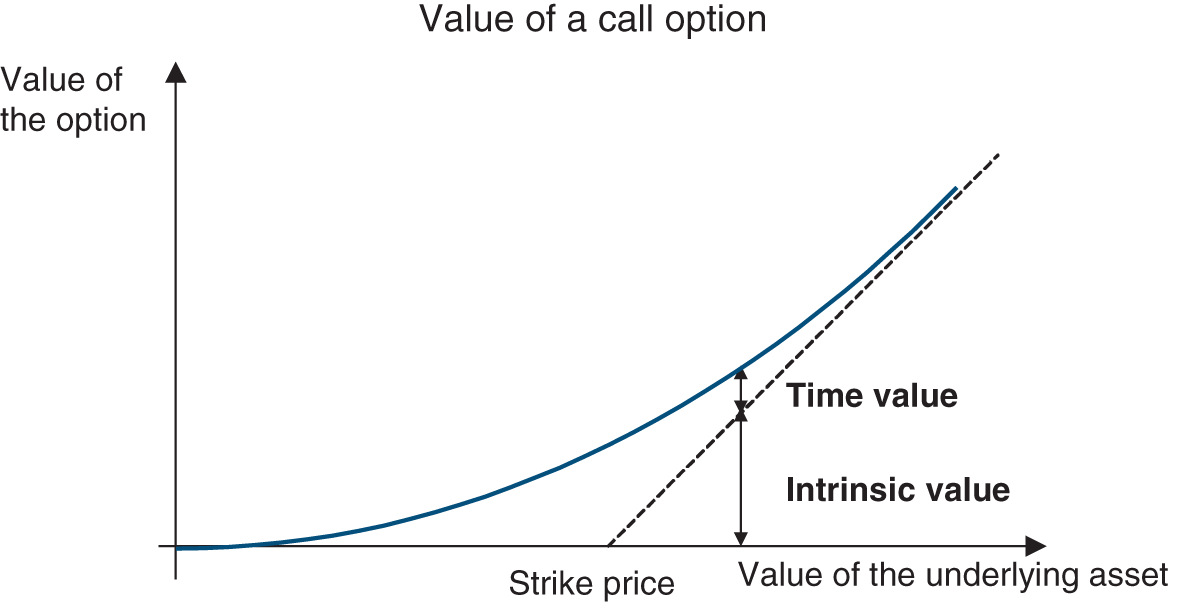
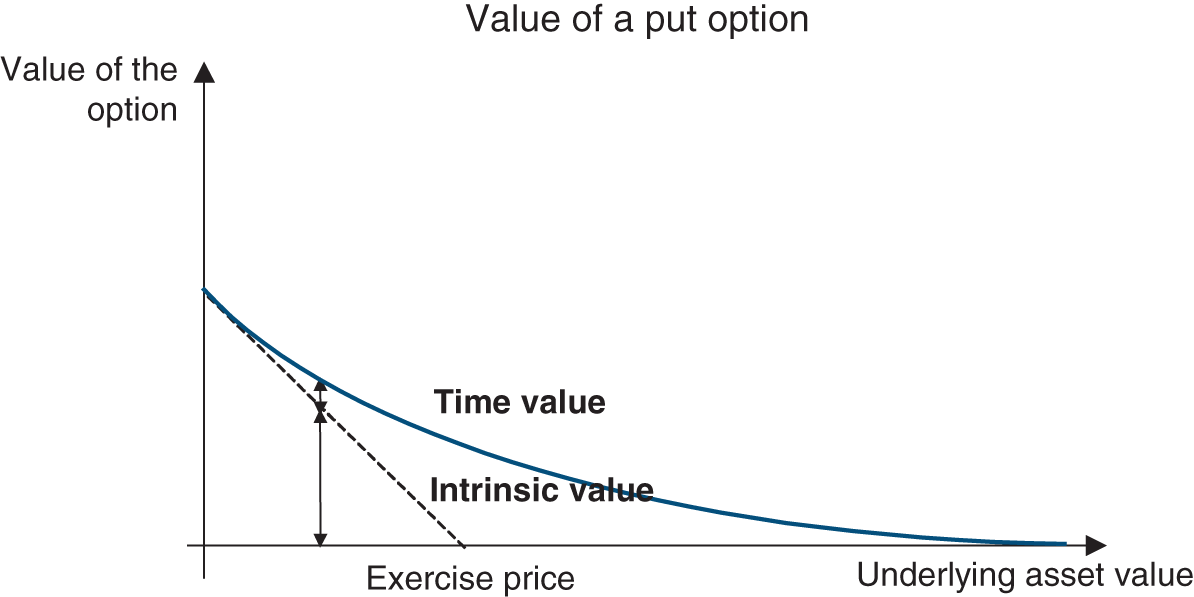
Time value diminishes with the passage of time, as the closer we get to the maturity date, the less likely it is that the price of the underlying asset will exceed the strike price by that date. Time value vanishes on the date the option expires.
This means that an option is worth at least its intrinsic value, but is there an upper limit on the option’s value?
In our example, the value at maturity of the call option on sterling is as follows:
- If sterling is trading above €1.15, the option is worth the current price of sterling less €1.15, i.e. its intrinsic value, which is below the value of the underlying asset.
- If sterling is below or equal to €1.15, the option will be worthless (i.e. no intrinsic value) and therefore even further below the price of the underlying asset.
This means that if the option’s value is equal to the price of the underlying asset, then all operators will sell the option to buy the underlying asset, as their gain will be greater in any case.
Section 23.4 PARAMETERS TO VALUE OPTIONS
There are six criteria for determining the value of an option. We have already discussed one of them, the price of the underlying asset. The other five are:
- the strike price;
- the volatility of the underlying asset;
- the option’s maturity;
- the risk-free rate;
- the dividend or coupon, if the underlying asset pays one out.
1/ PRICE OF THE UNDERLYING ASSET
As we saw earlier, all other criteria being equal, the value of a call option will be higher with a higher price of the underlying asset.
Symmetrically, the value of a put option will be lower with a higher price of the underlying asset.
2/ STRIKE PRICE
This is just common sense: the higher a call option’s strike price, the less chance the price of the underlying asset will exceed it. It is thus normal that the value of this call option is lower. However, the price of the put option will rise as the underlying asset can be sold at a higher price.
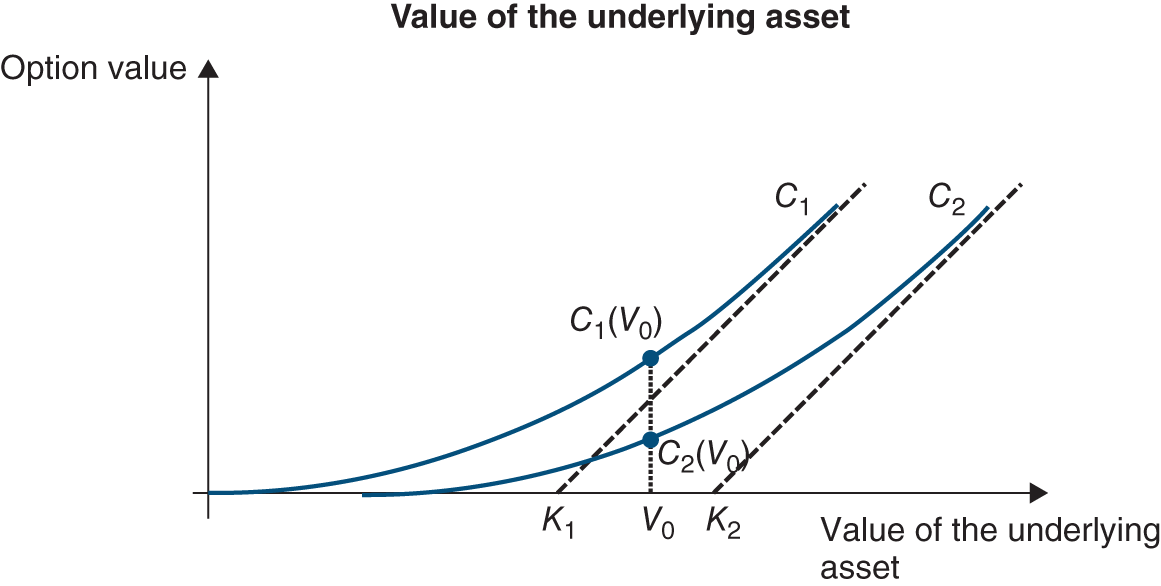
For the same value of the underlying asset, the value of a call option varies in the opposite direction to the strike price. The value of C2 is less than that of C1 as its exercise price is higher (K2 > K1)
3/ VOLATILITY IN THE VALUE OF THE UNDERLYING ASSET
Here again, this is easy to understand: the more volatile the underlying asset, the more likely it is to rise and fall sharply. In the first case, the return will be greater for the holder of a call option; in the second case, it will be greater for the holder of a put option. As an option is nothing more than pure remuneration of risk, the greater that risk is, the greater the remuneration must be, and thus the option’s value.
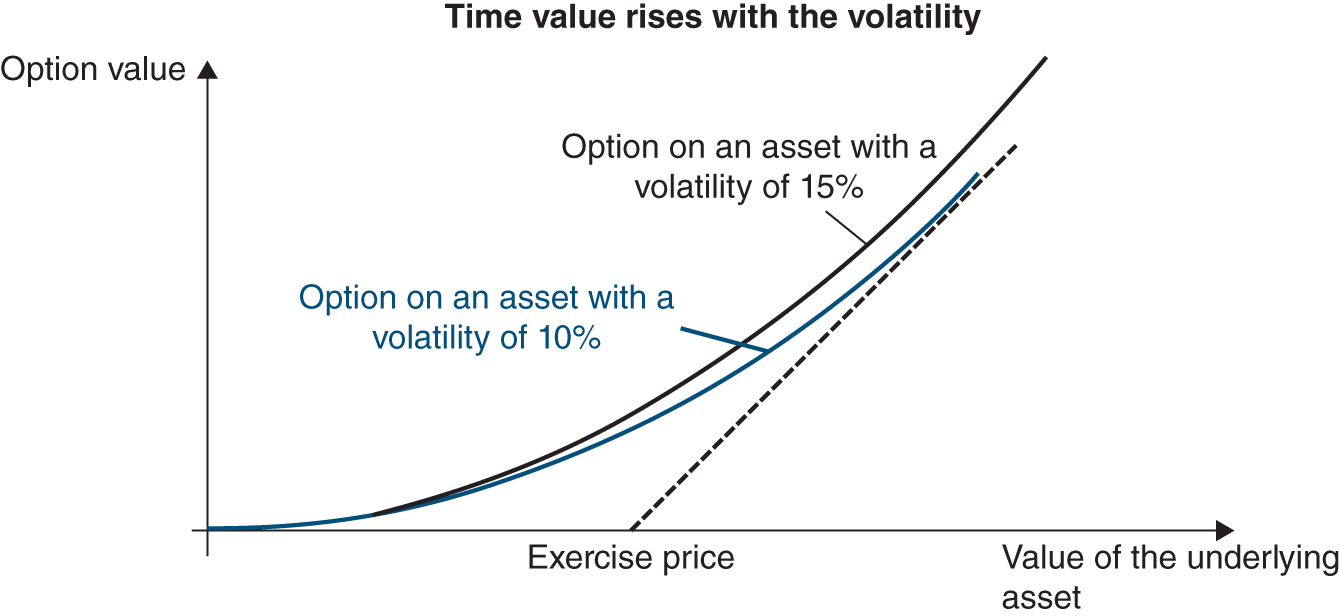
4/ THE TIME TO MATURITY
You can easily see that the further away maturity is, the greater the likelihood of fluctuations in the price of the underlying asset. This raises the option’s value.
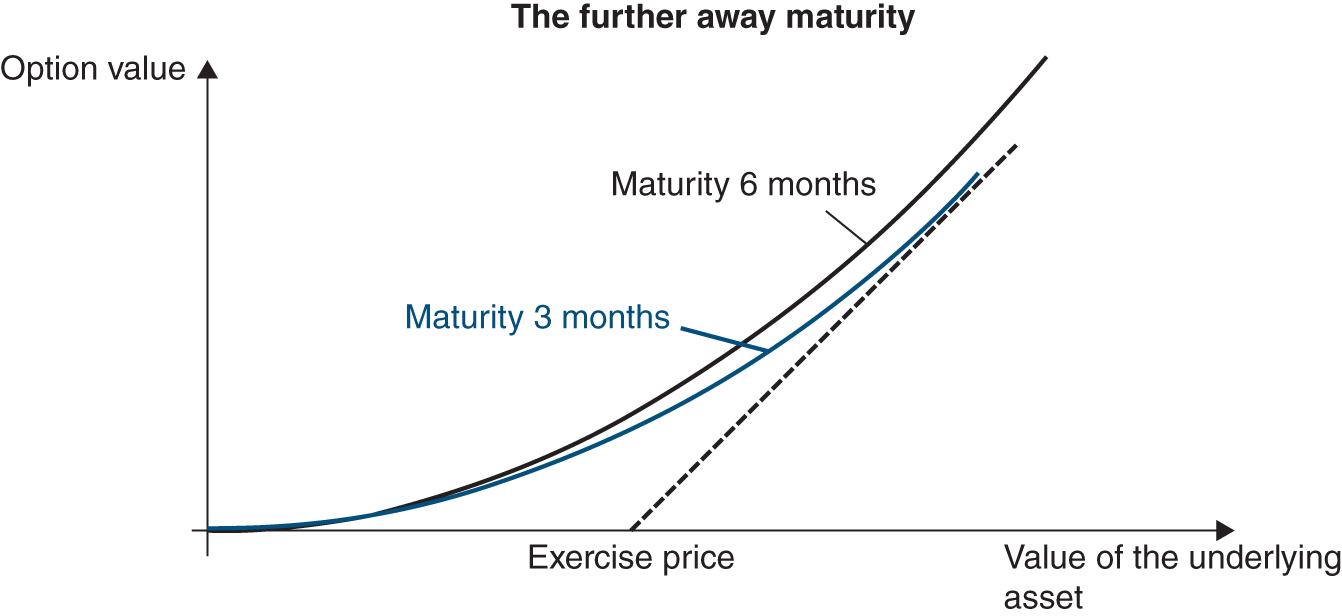
5/ THE RISK-FREE RATE
The buyer of the call option pays the premium, but pays the strike price only when exercising the option. Everything happens as if she was buying on credit until “delivery”. Consequently, the further away the maturity date on an option, the further away the payment of the acquisition price of the underlying asset. The holder of a call (put) option will thus have a cash advantage (disadvantage) that depends on the level of the risk-free rate.
Interest rates have much less influence on the value of an option than the other five factors.
6/ DIVIDENDS OR COUPONS
When the underlying asset is a stock or bond, the payment of a dividend or coupon lowers the value of the underlying asset. It thus lowers the value of a call option and raises the value of a put option. This is why some investors prefer to exercise their calls (on US-style options) before the payment of the dividend or coupon.
We can summarise the change in price of the option depending on the change in criterion in the following table:
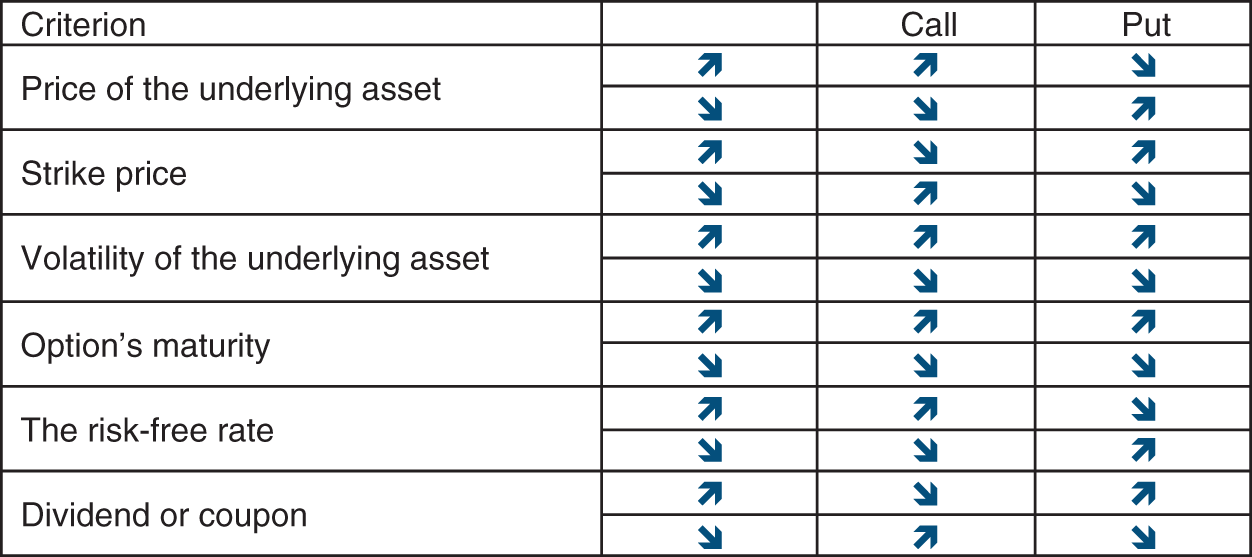
Section 23.5 METHODS FOR PRICING OPTIONS
1/ REASONING IN TERMS OF ARBITRAGE (BINOMIAL METHOD)
To model the value of an option, we cannot use discounting of future cash flow at the required rate of return as we have for other financial securities, because of the risk involved. Cash flow depends on whether or not the option will be exercised and the risk varies constantly. Hence, the further the option is into the money, the higher its intrinsic value and the less risky it is.
Cox et al. (1979) thus had the idea of using arbitrage logic in comparing the profit generated with options, with a direct position on the underlying asset.
Let’s take the example of a call option with a €105 strike price on a given stock (currently trading at €100) and for a given maturity.
Let’s also assume that there are only two possibilities at the end of this period: either the stock is at €90 or it is at €110. At maturity, our option will be worth its intrinsic value, i.e. either €0 or €5, or €0 or €20 if we held four options, for example, instead of just one.
We can try to obtain the same result (€0 or €20) in the same conditions using another combination of securities (a so-called replicating portfolio). If we achieve this result, the portfolio of four call options and this other combination of securities should have the same value. If we can determine the value of this other combination of securities, we will have succeeded in valuing the call option.
To do so, let’s say you borrow (at 5%, for example) a sum whose value (principal and interest) will be €90 at the end of the period concerned, and then buy a share for €100 today.
At the end of the period:
- either the share is worth €110, in which case the combination of buying the share and borrowing money is worth €110 − €90 = €20; or
- the share is worth €90, in which case the replicating portfolio is worth 90 − 90 = 0.
Since the two combinations – the purchase of four call options on the one hand, and borrowing funds and buying the share directly on the other hand – produce the same cash flows, regardless of what happens to the share price, their values are identical. Otherwise, arbitrage traders would quickly intervene to re-establish the balance. So what is the original value of this combination? Let’s look at it this way: €14.3 corresponds also to the value of the four call options. We thus deduce that the call option at a €105 strike is worth €3.58. We have valued the option using arbitrage theory.
“Delta” is the number of shares that must be bought to duplicate an option. In our example, four calls produce a profit equivalent to the purchase of one share. The option’s delta is therefore 1/4, or 0.25.
Hence:
Our example above obviously oversimplifies in assuming that the underlying asset can only have two values at the end of the period. However, now that we have understood the mechanism, we can go ahead and reproduce the model in backing up two periods (and not just one) before the option matures. This is called the binomial method, because there are two possible states at each step. By multiplying the number of periods or dividing each period into sub-periods, we can obtain a very large number of very small sub-periods until we have a very large number of values for the stock at the option’s maturity date, which is more realistic than the simplified schema that we developed above.
Here is what it looks like graphically:
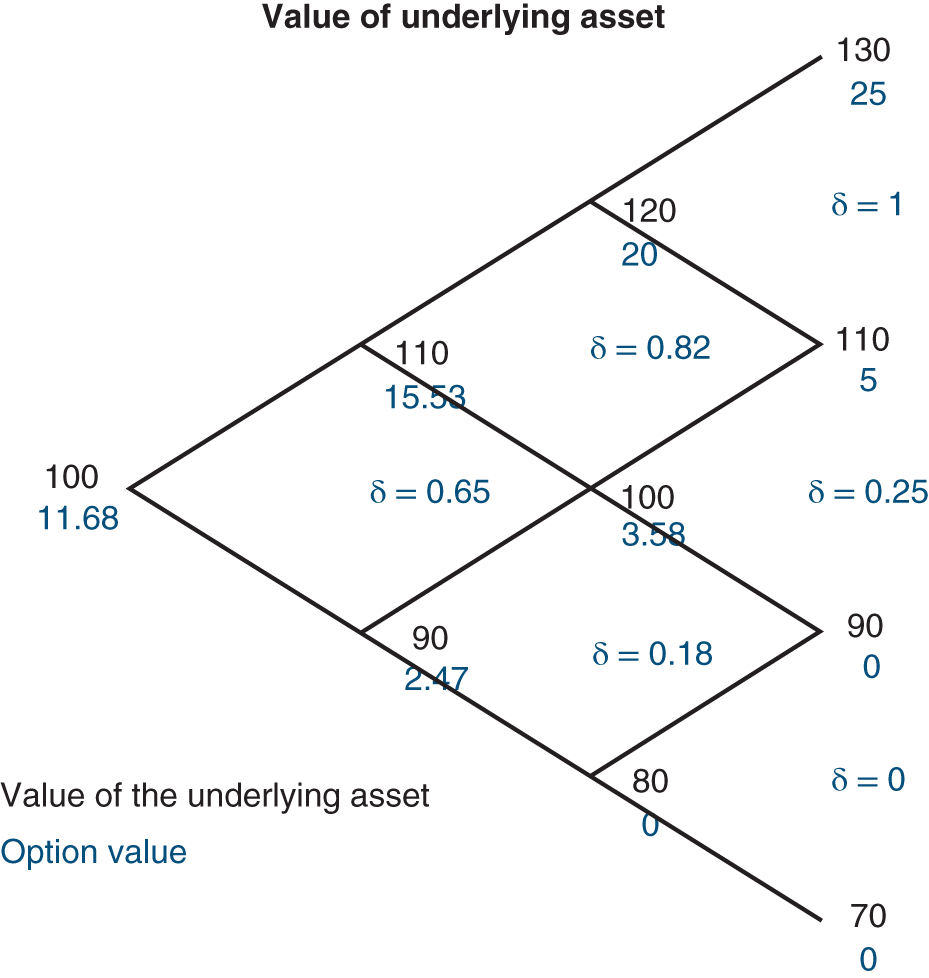
2/ THE BLACK–SCHOLES MODEL
In a now famous article, Fisher Black and Myron Scholes (1972) presented a model for pricing European-style options that is now very widely used. It is based on the construction of a portfolio composed of the underlying asset and a certain number of options such that the portfolio is insensitive to fluctuations in the price of the underlying asset. It can therefore return only the risk-free rate.
The Black–Scholes model is the continuous-time (the period approaches 0) version of the discrete-time binomial model. The model calculates the possible prices for the underlying asset at maturity, as well as their respective probabilities of occurrence, based on the fundamental assumption that this is a random variable with a log-normal distribution.
For a call option, the Black–Scholes formula is as follows:
with:
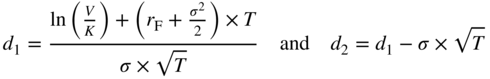
where V is the current price of the underlying asset, N(d) is a cumulative standard normal distribution (average = 0, standard deviation = 1), K is the option’s strike price, e is the exponential function, rF is the continual annual risk-free rate, s the instantaneous standard deviation of the return on the underlying asset, T the time remaining until maturity (in years) and ln the Naperian logarithm.
In practice, the instantaneous return is equal to the difference between the logarithm of the share price today and yesterday’s share price:
To cite an example: the value of a European-style nine-month call, with a strike price of €100, share price today of €90, a 3.2% risk-free rate and a 20% standard deviation of instantaneous return, is €3.3.
The formula for valuing the put option is as follows:
The reader should notice that N(d1) is the option’s delta, while ![]() represents the present value of the strike price.
represents the present value of the strike price.
Hence:
The Black–Scholes model was initially designed for European-style stock options. The developers of the model used the following assumptions:
- no dividend or coupon payout throughout the option’s life;
- constant volatility in the underlying asset over the life of the option, as well as the interest rate;
- liquidity of the underlying asset so that it can be bought and sold continuously, with no intermediation costs;
- that market participants behave rationally!
More complex models have been derived from Black and Scholes to surmount these practical constraints. The main ones are those of Garman and Kohlhagen (1983) for currency options and Merton (1976), which reflects the impact of the payment of a coupon during the life of a European-style option.
US-style options are more difficult to analyse and depend on whether or not the underlying share pays out a dividend:
- If the share pays no dividend, then the holder of the option has no reason to exercise it before it matures. They will sell their option rather than exercise it, as exercising it will make it lose its time value. In this case, the value of the US-style call option is thus identical to the value of a European-style call option.
- If the share does pay a dividend, then the holder of the call may find it worthwhile to exercise their option the day before the dividend is paid. To determine the precise value of such an option, we have to use an iterative method requiring some calculations developed by Roll (1977). However, we can simplify for a European-style call option on an underlying share that pays a dividend: the Black–Scholes model is applied to the share price minus the discounted dividend.
Of the six criteria of an option’s value, five are “given” (price of the underlying asset, strike price, maturity date, risk-free rate and, where applicable, dividend); only one is unknown: volatility.
From a theoretical point of view, the volatility should be the anticipated volatility and it would have to be constant for the Black–Scholes model to be applied. In practice, this is rarely the case: market operators adjust upward and downward the historical volatility that they calculated (over 20 days, one month, six months, etc.) to reflect their anticipation of the future stability or instability of the underlying asset. However, several classes of options (same underlying, different maturity or strike price) can be listed for the same underlying asset. This allows us to observe the implied volatility of their quoted prices and thus value the options of another class.
This is how anticipated volatility is obtained and is used to value options. This practice is so entrenched that options market traders trade anticipation of volatility directly.
Anticipated volatility is then applied to models to calculate the value of the premium.
The Black–Scholes model can thus be used “backwards”, i.e. by taking the option’s market price as a given and calculating implied volatility. The operator can then price options by tweaking the price on the basis of their own anticipation. They buy options whose volatility looks too low and sell those whose implied volatility looks too high.
It is interesting to note that, despite these simplifying assumptions, the Black–Scholes model has been de facto adopted by market operators, each of them adapting it to the underlying asset concerned.
3/ MODEL RISK
Options markets, whether organised (listed) or not (over-the-counter), have developed considerably since the mid-1970s, as a result of the need for hedging (of currency risks, interest rates, share prices, etc.), an appetite for speculation (an option allows its holder to take a position without having to advance big sums) and the increase in arbitrage trading.
In these conditions, a new type of approach to risk has developed on trading floors: model risk. The notion of model risk arose when some researchers noticed that the Black–Scholes model was biased, since (like many other models) it models share prices on the basis of a log-normal distribution. We have seen empirically that this type of distribution significantly minimises the impact of extreme price swings.
If returns actually followed a Gaussian distribution, the Dow Jones would change daily by more than 7% only once in 300,000 years. In the 20th century there were 53 such changes, and there have been 5 in 2020!
This has given rise to the notion of model risk, as almost all banks use the Black–Scholes model (or a model derived from it). Financial research has uncovered risks that had hitherto been ignored.
An anomaly in the options market highlights the problems of the Black–Scholes model. When we determine the implied volatility of an underlying asset (the only factor not likely to be observed directly) based on the price of various options having the same underlying asset, we can see that we do not find a single figure. Hence, the implied volatility on options far out-of-the-money or far in-the-money is higher than the implied volatility recalculated on the basis of at-the-money options. This phenomenon is called the volatility smile (because when we draw volatility on a chart as a function of strike price, it looks like a smile).
Section 23.6 TOOLS FOR MANAGING AN OPTIONS POSITION
Managing a portfolio of options (which can also be composed of underlying assets or the risk-free asset) requires some knowledge of four parameters of sensitivity that help us measure precisely the risks assumed and develop speculative, hedging and arbitrage strategies.
1/ THE IMPACT OF FLUCTUATIONS IN THE UNDERLYING ASSET: DELTA AND GAMMA
We have already discussed the delta, which measures the sensitivity of an option’s value to fluctuations in the value of the underlying asset. For calls and puts that are significantly out of the money, the value of the option may not change much when the underlying asset moves up or down. As the price of the underlying asset moves to a level substantially above the strike for calls or below the strike for puts, the option becomes more valuable and more sensitive to changes in the underlying asset.
Mathematically, the delta is derived from the option’s theoretical value vis-à-vis the price of the underlying asset and is thus always between 0 and 1, either positive or negative. Whether it is positive or negative depends on the type of option.
We have seen that, when using the Black–Scholes formula, the delta of a call option is equal to N(d1). The delta of a put option is equal to N(d1) − 1. This relationship is prized by managers of options portfolios, as it links the option’s value and the value of the underlying asset directly. Indeed, we have seen that the delta is, above all, an underlying equivalent: a delta of 0.25 tells us that a share is equivalent to 4 options. But above all, managers use the delta as an indicator of sensitivity: how much does the option’s value vary in euros when the underlying asset varies by one euro?
The delta of a call option that is far in-the-money is very close to 1, as any variation in the underlying asset will show up directly in the option’s value, which is essentially made up of intrinsic value.
Similarly, a call option that is far out-of-the-money is composed solely of its time value and a variation in the underlying asset has little influence on its value. Its delta is thus close to 0.
The delta of an at-the-money call option is close to 0.5, indicating that the option has as much chance as not of being exercised.
This is expressed in the following table:
| Out-of-the-money | At-the-money | In-the-money | |
|---|---|---|---|
| Call option | 0 < delta < 0.5 | delta = 0.5 | 0.5 < delta < 1 |
| Put option | −0.5 < delta < 0 | delta = −0.5 | −1 < delta < −0.5 |
The delta can also express probability of expiration in-the-money for options close to maturity and whose underlying asset is not too volatile: a delta of 0.80 means that there is an 80% probability that the option will expire in-the-money.
Unfortunately, the delta itself varies with fluctuations in the underlying asset and with the passing of time. Changes in the delta of an option create either a risk or an opportunity for investors and traders. Hence, the idea of measuring the sensitivity of delta to variations in the value of the underlying asset: this is what gamma does. Mathematically, it is none other than a derivative of the delta vis-à-vis the underlying asset, and is often called the delta of the delta!
The gamma of an option is largest near the strike price. A zero-gamma options position is completely immune to fluctuations in the value of the underlying asset.
2/ THE IMPACT OF TIME: THETA
Options are like people: they run down with time. Even if there is no change in the underlying asset price, the passage of time alone shows up in gains or losses for the option’s holder as a result of the decrease in the time value of the option.
Mathematically speaking, the theta is equal to the opposite of the derivative of the theoretical value of the option with respect to time. Theta measures how much an option loses in value if no other factors change.
3/ THE IMPACT OF VOLATILITY: VEGA
Vega is the derivative of the theoretical value of the option with respect to implied volatility. Vega is always positive for a call option, as for a put option, as we have seen that the time value of an option is an increasing function of volatility.
All other factors being equal, the closer an option is to being in the money (with maximum time value), the greater the impact of an increase in volatility.
While each of the tools presented here is highly useful in and of itself, combining them tells us even more. In practice, it is impossible to create a position that is neutral on all criteria at once. No return is possible when taking no risk. No pain, no gain! Hence, a delta-neutral position and a gamma-negative position must necessarily have a positive theta in order to be profitable.
4/ IMPLIED VOLATILITY
From 1990, the CBOE (Chicago Board Options Exchange) has calculated the VIX, an index of the implied volatility of the Standard & Poor’s 100, using at-the-money options with a maturity shorter than one month. The options on the S&P 100 are sufficiently liquid to consider this index representative of the implied volatility on the market.
The following graph shows the evolution of VIX from its initial launch.
Source: Data from FactSet, Bloomberg & Datastream
We will see in the following chapters the many applications of options in corporate finance:
- to raise financing (see Chapter 25);
- to resolve conflicts between management and ownership or between ownership and lenders (see Chapter 34);
- to hedge risks and invest (see Chapter 51);
- to choose investments (see Chapter 30);
- to value assets (see Chapter 31);
- to value the equity of a company (see Chapter 34);
- to take over a company (see Chapter 45).
This gives you an idea of the importance of options.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
Chapter 24. HYBRID SECURITIES
It’s a kind of magic
Before we begin the study of these different products, we caution the reader to bear in mind the following points:
- Some types of securities offer a lower interest rate in exchange for other advantages to the holder, and therefore give the impression of lowering the cost of financing to the company. It is an error to think this way. In markets in equilibrium, all sources of financing have the same cost if one adjusts for the risk borne by the investor.
- To know whether a source of financing is cheap or dear, one must look past the apparent cost to the overall valuation of the financing. Only if securities have been issued at prices higher than market value can one say that the cost of financing is indeed lower.
- With the exception of products that exactly match a particular market demand, sophisticated hybrid securities are costly to issue and sell. As such, they are a signal to investors that the company, or its majority shareholder, is having trouble attracting investors, perhaps because it is experiencing other difficulties.
- By emphasising the fundamental asymmetry of information between issuer and investor, agency theory and signalling theory are both very useful for explaining the appeal of products of this kind.
- Lastly, it must not be forgotten that corporate finance is not immune to fashion. Investors have a great appetite for novelty, especially if it gives them the feeling of doing high finance!
Section 24.1 WARRANTS
1/ DEFINITION
A warrant is a security that allows the holder to subscribe to another newly issued security (share, bond or even another warrant) during a given period, in a proportion and at a price fixed in advance.
Subscription warrants may be attached to an issue of shares or bonds, in which case the issue is said to be one of “shares cum warrants” or “bonds cum warrants” or “convertible bonds cum warrants”. Attached warrants to buy shares may be called an “equity sweetener” or “equity kicker”. Warrants can also be issued and distributed to existing shareholders at no charge. Once securities with attached warrants have been issued, the whole is split into its two component parts: the shares or bonds become traditional securities and the warrants take on a life of their own. The warrants are traded separately after issue.
As an illustration, Marlin issued free equity subscription. A warrant allowed the holder to subscribe to one Marlin share at NZ\$1.28 on 20 May 2022. In June 2021 the Marlin warrants were trading at NZ\$0.24, whereas Marlin shares were trading at NZ\$1.45.
As liquidity in the stock and bond markets has increased, financial institutions have taken the opportunity to issue warrants on existing securities independently of the company that issued the underlying shares. These securities are also called covered warrants because the issuing institution covers itself by buying the underlying securities on the market.
Warrants ordinarily involve a transaction between one investor and another and therefore play no direct role in financing a business. There being no limits to the imagination, some players have not hesitated in creating warrants on baskets of existing securities (such as indices). Thus, a warrant on a basket of different shares gives one the right to acquire, during a given period of time, a lot consisting of those shares, in proportions and at an overall price fixed in advance.
2/ VALUE
Conceptually, a warrant is similar to a call option sold by a company on shares in issue or to be issued. The exercise price of this option is the price at which the holder of the warrant can acquire the underlying security; the expiry date of the option is the same as the expiry date of the warrant.
A warrant, however, has a few particular characteristics that must be taken into account in its valuation:
- It normally has a long life (typically two to three years but sometimes much more, six years for Prologue), which increases its time value and makes it more difficult to accept the assumption of constancy in interest rates and volatility used in the Black–Scholes model.
- The underlying asset is more likely to pay a periodic return during the time the warrant is held:
- For an equity warrant, the payment of dividends on the underlying share lowers the value of that share and thereby reduces the value of the warrant. More generally, any transaction that changes the value of the share affects the value of the warrant.
- For a debt warrant, the price of the underlying bond varies over time and, as we saw in Chapter 20, the closer a bond comes to maturity, the more its market price tends towards its redemption price. Its volatility gradually declines, making the Black–Scholes model, which assumes constant volatility, inapplicable as stated.
- Lastly, in the case of subscription warrants, the dilution associated with exercise of the warrants entails a gradual change in the value of the underlying security. When investors exercise warrants, the number of outstanding shares increases and the issuing firm receives the strike price as a cash inflow. When investors exercise call options, no change in outstanding shares occurs as call options are options on shares that already exist and not on new shares to be issued; hence, the firm receives no cash.
To get round these difficulties, traders use models derived from the binomial and Black–Scholes models, taking into account the fact that the exercise of warrants can create more shares and thus affect the stock price.
3/ THEORETICAL ANALYSIS
Agency theory offers an almost “psychological” approach to these securities. They are seen as a preferred means of resolving conflicts between shareholders, lenders and managers.
Take a bond with attached equity warrant as an example. A hybrid security of this kind may seem unnatural since it combines a low-risk asset (bond) with a high-risk asset (share).
However, there is something in it for each of the parties.
The company’s managers benefit from the flexibility that warrants provide, since the company can set bounds on the date of the capital increase (by setting the subscription period of the warrant) and the amount of funds that will be raised (by setting the exercise price and the number of warrants per bond at appropriate levels). The amount of funds raised in the form of bonds can be completely different from the amount potentially raised later in the form of shares. Furthermore, the company may be able to use the funds from both sources for several years, since the warrants may be exercised before the bonds are paid off.
A company that wants to accomplish the capital increase part of the issue quickly will set an exercise price barely above, or even below, the current price of the share. If it chooses, it can also move up the beginning of the subscription period. If it prefers to bring in a greater amount of funds, it will increase the number of warrants per bond (which must then have a lower yield to maturity if equilibrium is to be maintained) and potentially raise the exercise price of the warrants.
Because it entails selling an option, though, the opportunity cost of a warrant can be substantial. Take the case of a company that has sold for €10 the right to buy one share at €100. Suppose that at the time this warrant becomes exercisable the shares are trading at €210. A straight capital increase without a rights issue at a very slight discount to the share price would bring in, say, €205 per share, whereas exercise of the warrants will bring in €110 per share all told. The opportunity cost is €95 per share.
Stock market history has shown that exercise of warrants can never be taken for granted. After the steep decline in stock markets in 2007/2009, firms that issued warrants before this period have a very low probability of being able to raise equity thanks to these warrants.
The holders of bonds with attached equity warrants, if they keep both securities, are both creditors and potential shareholders. As creditors, they benefit from a small but relatively certain yield; as potential shareholders, they have hopes of realising a capital gain.
In a context of rising interest rates and falling share prices, however, holders of bonds cum warrants suffer the downside risks of both debt and equity securities, instead of combining their advantages.
On the other hand, the holders of the bonds may be different from the holders of the warrants. The bonds may end up with investors preferring a fixed-rate security, while the warrants go to investors seeking a more volatile security.
In appearance only, existing shareholders retain their proportionate equity stake in the company. The warrant mechanism makes for gradual dilution over time. An issue of bonds with equity warrants allows existing shareholders to maintain their control over the company with a smaller outlay of funds, since they can buy the warrants and resell the bonds. If they do this, the securities they end up holding will be much riskier overall because the bonds will no longer be there to cushion fluctuations in the value of the warrants.
The dilution problem is postponed. When the warrants are exercised, they may have risen in value to such an extent that existing shareholders can pay for virtually all of their proportionate share of the capital increase by selling their warrants in order to finance their share subscription.
4/ PRACTICAL USES
Warrants are increasingly widely used in corporate finance:
- By a company in difficulty that wants to raise fresh capital. Before going ahead with a capital increase, the company decides to make a bonus distribution of warrants to existing shareholders. In practice, the shareholders are giving themselves these warrants. They can then speculate more readily on the company’s turnaround. This was the case for CGG in 2018.
- When creditors are cancelling debts due to them, shareholders may give them equity warrants in return. The value of these warrants is virtually nil at the start, but if the company regains its footing, the warrants will rise in value and make up for some or all of the loss on the cancelled debts. A deal of this kind is the way to reconcile the normally divergent interests of creditors and shareholders. In modern finance, this technique replaces the “return to better fortune” clause in loan agreements.
- In a tender offer for shares of company A in exchange for shares of company B, shareholders of A may be offered not only shares of B but also warrants for shares of B.
- In a leveraged buyout (LBO, see Chapter 47), warrants may be used to offer an additional reward to holders of mezzanine debt or even to management (another instance of an “equity kicker”).
- As a management-incentivisation tool, warrants can be used as an alternative to stock options or performance shares. The key difference lies in the fact that warrants have to be acquired by management (whereas stock options or performance shares are distributed free of charge).
5/ REDEEMABLE WARRANTS
Redeemable warrants are warrants that can be redeemed by the issuer. The company can redeem, at nominal price, the warrants in case the share price exceeds a certain threshold. In practice this means that the company can force the exercise of the warrants after a certain time if conversion conditions are met, as the redeemable warrant holder will prefer exercising rather than being redeemed at nominal price.
This is equivalent to a “soft call” clause in a convertible bond contract (see below).
This product is usually tied to a bond and issued by mid-sized companies to refinance bank loans. Some groups issued bonds cum redeemable warrants subscribed by banks that kept the bonds and sold the warrants to the management, thus partially replicating the management packages of LBOs.
Section 24.2 CONVERTIBLE BONDS
1/ DEFINITION
A convertible bond is like a traditional bond except that it also gives the holder the right to exchange it for one or more shares of the issuing company during a conversion period set in advance.
Source: Data from Dealogic
As an example, in April 2021 the medtech Predilife issued a convertible bond with the following characteristics:
The conversion period is specified in the bond indenture or issue contract. It may begin on the issue date or later. It may run to the maturity date, or a decision may be forced if the company calls the bonds before maturity, in which case investors must choose between converting them into shares or seeing them being redeemed in cash.
The bond may be convertible into one or more shares (612.5 shares for each bond in our example). This ratio, called the conversion ratio,1 is set at the time of issue. The conversion ratio is adjusted for any equity issues or large buy-backs above market price, mergers, asset distributions or distributions of bonus shares in order to preserve the rights of holders of the convertibles as if they were shareholders at the time of issue.
The conversion premium is the amount by which the conversion price exceeds the current market price of the share. A conversion premium is typical. In our Predilife example, the conversion premium is 38%.2 Since Predilife offered no redemption premium, its shares must rise 38% by the maturity date of the bonds for investors to be willing to convert their bonds into shares rather than redeem them for cash. The calculation is slightly different when a redemption premium is involved.
Some convertible bonds are issued with a call provision that allows the issuer to buy them back at a predetermined price. Holders must then choose between redeeming for cash or converting into shares. The indenture may provide for a minimum period of time during which the call provision may not be exercised (“hard non-call” period, usually at least one year) and/or set a condition for exercising the call provision, such that the share price exceeds the conversion price by more than a percentage, most of the time 30%, for more than 10 days (“soft call” provision). The Predilife convertible bond does not have a soft call provision.
In some cases, the issuer may, upon conversion at the holder’s request, provide either newly issued shares or existing shares held in portfolio – for example, following a share buy-back, as is the case for the Predilife bond issuance. In other cases, the issuer has the right to provide the counter value in cash of the shares that were to be given for repayment. This makes it possible to limit the dilution of current shareholders.
As with other debt instruments, convertible bonds can be green if the proceeds are used for energy transition investments (Neoen, EDF), or sustainable (Schneider), if the return paid to investors is increased in case certain ESG objectives are not met (energy consumption, CO2 emissions, increasing gender diversity, etc.).
Convertible bonds must not be confused with the similar-sounding exchangeable bonds, which are pure debt securities from the point of view of investors. We are going to study them in Section 24.4.
2/ VALUE
The value of a convertible bond during its life is the sum of two components:
Convertible bond = bond value + call option
- The value of the straight bond alone is called the bond value of the convertible bond. It is calculated by discounting the future cash flows on the bond at the market interest rate, assuming no conversion. The bond value thus represents a minimum value: the convertible will never be worth less than this floor value, even if the share price falls significantly. It also cushions the impact of a falling share price on the price of the convertible. Bear in mind, though, that investment value is not a fixed number but one that varies as a function of changes in interest rates.
- The option value. To the bond value is added the value of the conversion option. The higher the share value exceeds the redemption price of the convertible bond, the higher the value of the conversion option, and the lower the share value falls below the redemption price of the convertible bond, the lower the value of the conversion option.
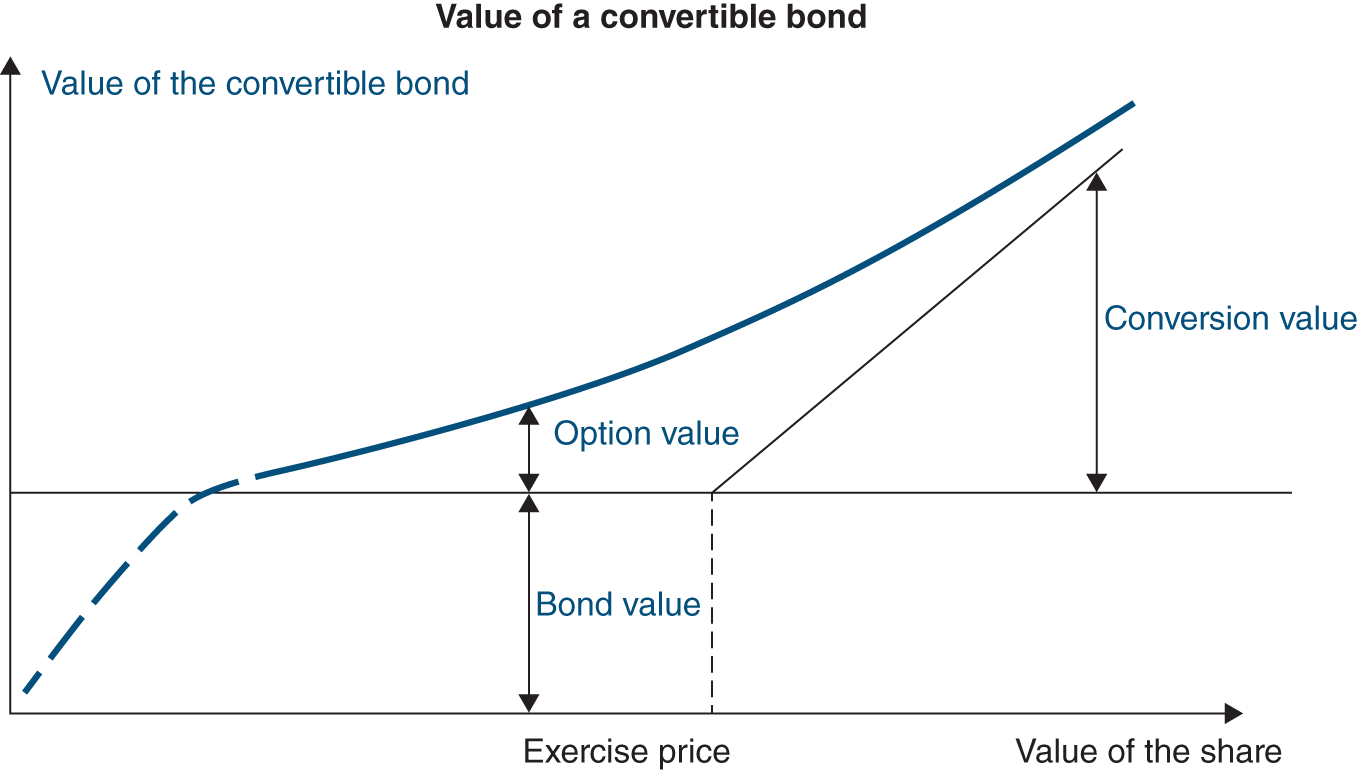
Whenever the share price is well above the redemption value of the convertible bond – as in the “share” zone of the following chart for Rémy Cointreau in summer 2020 – the convertible bond behaves more and more like the share because the probability that it will be converted into shares is very high.
In the “bond” zone, the convertible bond behaves essentially like a bond because, given the level and trend of the share price, the probability of conversion is low. The price of the convertible bond is close to its investment value. This was the case for the Rémy Cointreau convertible bond in the months following its issue in the autumn of 2016.
In the “hybrid” zone, the value of the convertible reflects the simultaneous influence of both the level of interest rates and the price of the underlying security, as for the Rémy Cointreau convertible bond in spring 2020.
There can also be a high-risk zone for the convertible bond if the share price has fallen sharply. Heavy doubts appear as to the company’s ability to repay its debts. The price of the convertible bond adjusts downwards accordingly, until it offers a yield to maturity consistent with the risk of default by the issuer.
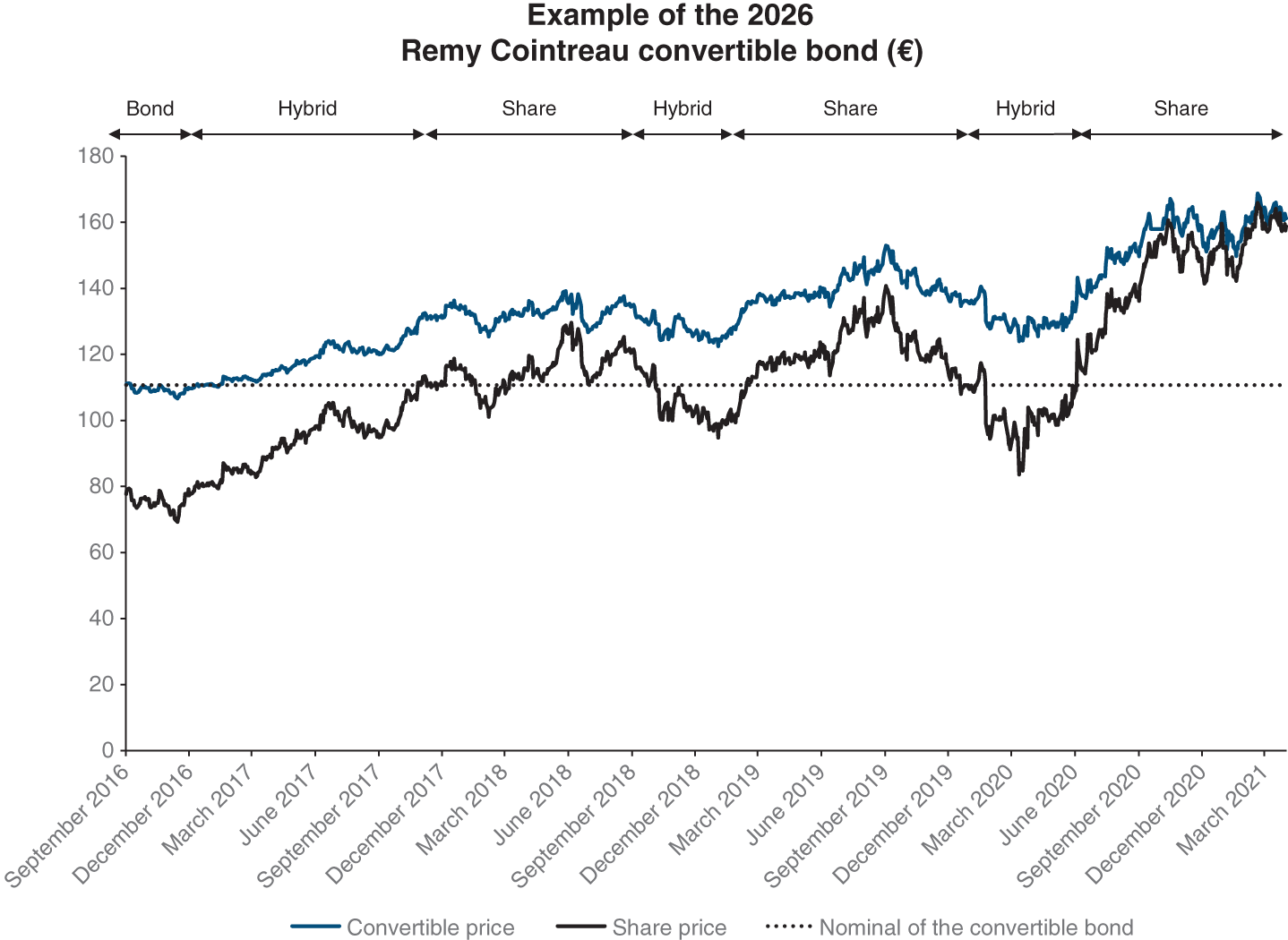
Source: Data from Bloomberg
At issue, the bond value most often represents 85–95% of the value of the convertible bond and the call option 5–15%. The lower the conversion premium, the closer the convertible bond will be to a share since conversion into shares will be very likely. The coupon of the convertible bond may therefore be low. Conversely, the higher the conversion premium, the closer the convertible bond will be to a bond requiring a higher yield. By balancing these characteristics of the convertible bond, the CFO will be able to tailor the convertible bond to the cash flow profile of the company and the dilution appetite of its shareholders.
3/ SYNTHETIC BONDS
In the mid-2010s, peculiar convertible bond issues were implemented with the following principle: the firm issues convertible bonds to investors and acquires call options at the same time (from one or several banks) that mirror the options imbedded in the convertible bonds. The convertible bonds and options have the specificity of offering only a cash settlement (the counter value in cash of the shares being paid in case the option is exercised). For the firm, the bundling of the issuance of a convertible bond and the acquisition of a call replicates the cash flows of a plain vanilla bond exactly. For the company, it is the same as issuing a plain vanilla bond.
This product can be attractive when market appetite for convertible bonds is high. There may then be a true arbitrage opportunity that allows the firm to sell the call option to investors at a higher price than the price it paid the banks. In this case, the yield of the instrument, called an Equity Neutral Convertible Bond (ENCB), will come out as lower than that of a traditional bond. This combination can also be used for firms that do not have access to the bond market.
Companies that have issued synthetic bonds include LVMH, National Grid, Total, Iberdrola, Michelin, and HDFC, amongst others.
4/ THEORETICAL ANALYSIS
Unlike a bond with attached equity warrants, a convertible bond is an indivisible product. The straight bond cannot be sold separately from the call option.
For the investor, the convertible bond is often presented as a miracle product, with downside protection by virtue of its debt component and upside potential by virtue of its equity component.
In much the same fashion, the convertible bond is pitched to issuers as the panacea of corporate finance. Initially, it enables the company to issue debt at an interest rate lower than the normal market rate; at a later point, it may enable the company to issue fresh equity at a price higher than the current share price.
No! There are no miracles in finance. At best, one can find mirages, and this is one. If the company is able to issue bonds at an interest rate below its normal cost of debt, it is because it has agreed to issue shares in the future at a price below the share value at that time – necessarily below, or conversion would not take place. Current shareholders will therefore be diluted on poor terms for them. In addition, the argument of a lower rate is true only in terms of cash, as under IFRS the current interest rate at which the company could issue an ordinary bond must be applied when recording associated interest expenses in the P&L, even if it actually pays a lower interest rate on its convertible bonds.
Similarly, if investors are getting a call option on the share, it is because in return they accept a lower rate of return on the bond than the issuer-specific risk would justify.
The apparent cost of the convertible bond is low only because its true cost is partly hidden. The company is selling investors call options, which they pay for by accepting a lower interest rate on the bonds than the company could normally obtain given its risk.
The cost of a convertible bond may be calculated in intuitive fashion as a weighted average of the cost of equity and the cost of debt. The weighting corresponds to the probability that the convertible will actually be converted. This probability is not hard to estimate if one assumes that returns on the share are normally distributed (then the expected yearly increase in share price is equal to the cost of equity less the dividend yield).
Equilibrium market theory is not of much help in explaining why convertible bonds, which are no more than a combination of two existing products, should themselves exist. Agency theory and signalling theory – together with the “matching hypothesis” – are far more useful in understanding the usefulness of convertibles.
- According to agency theory, a convertible bond is a mode of resolving conflicts between shareholders and creditors. Managers of leveraged companies can be tempted to undertake risky investments that increase shareholder wealth at the creditors’ expense. With this fear in mind, creditors refuse to finance the company except via convertible bonds. Creditors will then have some protection, since the convertible gives them the option of becoming shareholders if there are transfers of value working against them as creditors. A heavily indebted company may have to pass up highly profitable investment projects if it cannot obtain bank financing that would not put too great a strain on its cash flow at the start. With its low apparent interest cost, the convertible bond is an attractive alternative. A convertible bond also helps in resolving conflicts between shareholder-managers and outside shareholders. Shareholder-managers of a company with convertible bonds outstanding will hesitate to divert company resources to private use at the expense of other shareholders, since they know that would increase the probability of having to redeem the convertibles in cash. If the company is already carrying a sufficiently high debt load, redemption could put it in difficulty and threaten the managers’ position, so they are deterred from taking such action.
- The matching hypothesis provides another contribution to the explanation of why convertible bonds exist. A young, fast-growing company or one with limited financial resources will avoid taking on too much debt, as its cash flow is likely to be highly variable and its cost of debt, given its short history, likewise high. In these cases, it makes sense to issue securities whose cash flows match those of the firm.
- A fast-growing company will have little inclination to issue more shares, either because it believes its shares are undervalued or because it fears sending out a negative signal (see Chapter 38). That leaves only convertible bonds. Investors, relieved that the signal associated with a capital increase has not been sent, will welcome an issue of convertibles (e.g. Voltalia). This is what the signalling theory assumes.
Taken together, these three explanations provide good reasons for issues of convertible bonds by smaller companies that are growing rapidly, are already heavily indebted or have assets that are quite risky. We could also add another explanation, which is commonly known as the “backdoor equity” hypothesis. Young, growing firms cannot usually issue debt because of the high financial distress costs. At the same time, they may be unwilling to issue equity if current stock prices are too low. Thus, convertible bonds could offer a good compromise solution. Convertible bonds cause expensive dilution, but it occurs when the firm can afford it!
The market for convertibles is also supplied by large groups (e.g. Safran, Schneider), which use it to raise funds from specialised investors that invest only in convertible bonds. For these large groups, convertibles offer a way of diversifying the investor base and raising money in large quantities more easily. Lastly, groups in financial difficulty will resort to issuing convertibles when the equity market is closed to them (Just Eat).
Section 24.3 PREFERENCE SHARES
The securities called preference shares (a term prevailing in the UK) or preferred shares (a term prevailing in the US) enjoy economic advantages over ordinary shares, typically in return for a total or partial absence of voting rights.
1/ DEFINITION
Preference shares are created on the occasion of a capital increase by the decision of the shareholders at an (extraordinary where applicable) general meeting.
The advantages conferred on preference shares may include:
- a claim to a higher proportion of earnings than is paid out on other shares;
- priority in dividend distributions, meaning the dividend on preference shares must be paid before any ordinary dividend is paid on other shares;
- a cumulative dividend, so that if earnings are insufficient to pay the preference dividend in full, then the amount not distributed becomes payable from future earnings;
- a firm cannot go into default if it misses paying some dividends;
- rating agencies and financial analysts consider preference shares a part of equity (thus improving the rating of the company).
At the same time, there are two important disadvantages in issuing preference shares.
- for the issuer – because it adds a layer of complexity; and
- for the investors – because they may have limited voting rights, although in private companies they may have multiple voting rights.
We should note here that the term “preferred securities” (often shortened to just “preferreds”) is much broader in scope and may encompass convertible bonds and subordinated debt securities as well as preference shares without voting rights. The reader is advised to look closely at the detailed characteristics of any security called a “preferred” and not to assume that it is necessarily a preference share.
Special features can be added to preference shares to make them more attractive to investors or less risky to issuers:
- adjustable-rate preference share: the dividend rate is pegged to an index rate, such as a Treasury bill or Treasury bond;
- participating preference share: the dividend is divided into a fixed and a variable component. The latter is generally set as a function of earnings;
- trust preference share: the dividend on these stocks is tax-deductible like interest expenses. Firms issuing this security get the tax shield of debt and keep leverage low (because preference shares are treated like equity by analysts and rating agencies).
2/ VALUE
It is complex to generalise the valuation formula of preference shares as the term covers products that can have very different features. Preference shares will normally be valued just like ordinary shares (taking into account the potential higher dividend stream). The value of the preference share will be equal to the value of the ordinary share to which you need to:
- add the value of the advantages granted;
- deduct a liquidity discount for public companies (as the preference share will generally have low liquidity). This discount is almost always observed in trading prices;
- potentially deduct the value of the voting right.
As each of these elements is difficult to assess, the value of the preference share will be quite uncertain.
3/ THEORETICAL ANALYSIS
(a) For the company
Preference shares can enable a company, which is in difficulty but has a good chance of recovering, to attract investors by granting them special advantages.
Banks are often issuers of preference shares because these securities are classified by central banks as part of the bank’s own funds for the purpose of determining its net capital. This is so even though the preference share pays a constant annual dividend expressed as a percentage of par value, which gives it a strong resemblance to a debt security. Analysts are not fooled; for their purpose, preference shares are reclassified as debt.
Against these advantages, preference shares also present several drawbacks:
- They cost more than a traditional capital increase: the preference dividend is higher than the ordinary dividend, whereas the preference share itself is usually worth less than the ordinary share because of its lesser liquidity.
- Their issuance entails complications that are avoided with an ordinary capital increase, such as calling a special shareholders’ meeting.
- Furthermore, understanding such issues can be quite difficult. Preference shares frequently trade at a steep discount to theoretical value because holders demand a big premium over market value before they will sell or exchange them.
(b) For current shareholders
For a majority shareholder, issuing preference shares makes sense only if those shares have no voting rights. When this is true, a capital increase can be accomplished without diluting their control of the company. A company with family shareholders may issue preference shares in order to attract outside financial investors without putting the family’s power over the company in jeopardy. For the minority shareholder, this seems to us to be a second-best solution: the only way to strengthen shareholders’ equity when the majority shareholder does not want to follow a capital increase or be diluted. It is just as if the company’s cost of capital had been raised.
The flexibility offered by preference shares is undoubtedly of interest to unlisted companies. Indeed, they make it possible to organise corporate governance between the shareholders involved in management and the financial shareholders. We can therefore see them flourish in private equity (to finance start-up, development, transmission or the acquisition of a company), and in particular LBOs. Today, issuances of new preference shares have virtually disappeared from stock markets, which prefers a single line of listing per company with a large volume of transactions and equality of shareholders. Intesa Sanpaolo thus imposed the merger of its two types of shares in 2018.
Section 24.4 OTHER HYBRID SECURITIES
1/ HYBRID BONDS
Also called deeply subordinated bonds, or simply hybrids, they present the following features:
- Very long maturity (more than 50 years) or no duration (i.e. perpetual). Some hybrids include a hard non-call provision prohibiting the firm from redeeming the issue before a certain date. Generally the interest rate increases in time (step-up), which encourages the firm to redeem the bonds as the price becomes prohibitive (but there is no legal requirement to do so).
- Ranking: in case of liquidation, the securities must rank senior only to share capital.
- Conditional payment of interest: under certain conditions, such as non-payment of dividends to shareholders, payment of the coupon/dividend to investors must be left at the issuer’s entire discretion. In certain cases, the non-payment must be compulsory if some debt ratios are not satisfied.
- No voting rights is attached.
- The issuer may commit to redeeming the issue only by issuing equity or a similar hybrid instrument.
- Depending on the exact features, some issues may be classified as equity under IFRS as there is no commitment to redeem and as payment of interest may be suspended. Nevertheless, IASB is considering changing its stance on this subject.
Conceptually, these are nothing other than very long-term debt securities, whose extremely subordinated nature could lead to them being assimilated, from an accounting point of view, to equity, which in our view is wrong.
Rating agencies adopt a hybrid treatment by restating these issues in one part debt and one part equity (the equity content). So, for example, Moody’s carries out a precise analysis of the terms and conditions of the issue (in accordance with a pre-established table) and classifies the issue in a basket (B, C or D) to which is attached an equity content (25%, 50% or 75%) for investment grade firms. Issues made by non-investment grade issuers are considered as 100% debt by Moody’s.
Industrial groups use hybrid bonds either to diversify their investor base (Orange, Engie which issued a green hybrid) or to secure their rating and strengthen their capital structure (Arkema, Unibail-Rodamco-Westfield, Abertis).
2/ MANDATORY CONVERTIBLES
Unlike convertible bonds, for which there is always some risk of non-conversion, mandatory convertibles are necessarily transformed into equity capital (unless the issuing company goes bankrupt in the meantime) since the issuer redeems them by delivering shares; no cash changes hands at redemption.
The value of a bond redeemable in shares is the present value of the interest payments on it plus the present value of the shares received upon redemption. In pure theory, this is equal to the value of the share increased by the present value of the interest and decreased by the present value of the dividends that will be paid before redemption. The discount rate for the interest is the required rate of return on a risky debt security, while the discount rate for the dividends is the company’s cost of equity.
Under IFRS, their issue value is broken down between the present value of interest shown as debt and the balance in shareholders’ equity.
Mandatory convertibles are not a very attractive product on the financial markets (there is no suspense, unlike the convertible bond!), so it is not very common there. Rather, it is used in very specific arrangements for unlisted companies, often with tax or legal concerns. In 2020, ArcelorMittal issued a mandatory convertible for which the conversion parity was linked to the share price. This issue has allowed to differ the dilution of the Mittal family in the capital.
For tax purposes, bonds redeemable in shares are treated as bonds until they are redeemed, and subsequently as shares.
They have been issued by a number of companies, large and small, to raise capital, including Texas Instruments, General Motors, Citicorp, Lafarge, AXA and Sears.
3/ EXCHANGEABLE BONDS
An exchangeable bond is a bond issued by one company that is redeemable in the shares of a second company in which the first company holds an equity interest. Thus, while a convertible bond can be exchanged for specified amounts of common stock in the issuing firm, an exchangeable bond is an issue that can be exchanged for the common stock of a company other than the issuer of the bond.
At maturity, two cases are possible. If the price of the underlying shares has risen sufficiently, then holders will exchange their bonds for the shares; the liability associated with the bonds will disappear from the issuer’s balance sheet, as well as the underlying shares. If the price has not risen enough, then holders will redeem their bonds for cash and the issuer will still have the underlying shares. In neither case will there be any contribution of equity capital. An exchangeable bond is therefore like a collateralised loan with a call option for the holder on securities held in the company’s portfolio.
For the investor, a bond issued by company X that is exchangeable for shares of company Y is very close to a convertible bond issued by Y. The only thing separating these two financial instruments is the default risk of X versus that of Y.
By way of example, in February 2021 Bigben issued a bond exchangeable for shares in Nacon (for a total of 10.67% of Nacon). Bonds are exchangeable with shares with a premium of 16% for five years. This issue raised €87m for the group at an apparent interest rate of 1.70%. The quid pro quo is obviously twofold: for one thing, Bigben cannot be sure of having unloaded a part of its holding in Nacon; for another, if it does succeed in disposing of that stake, it will have let it go at a price below its market value. But on the face of it, Bigben has obtained long-term financing with a low interest rate.
For the investor, a bond issued by Bigben that is exchangeable for Nacon shares and a convertible bond issued by Nacon are very similar financial instruments; only the risk of default differentiates them (Bigben or Nacon).
SUMMARY
QUESTIONS
EXERCISE
ANSWERS
BIBLIOGRAPHY
NOTES
Chapter 25. SELLING SECURITIES
Chapter 25
SELLING SECURITIES
Get ’em while they’re hot!
Now that we have studied the properties of the various financial securities, let’s see how companies sell them to investors. Bank finance was beautiful in its simplicity – whenever a company needed funds, it turned to its bank. Now that direct financing has become more common, companies can raise funds from a great many investors whom they do not necessarily know. That means they have to market their financing!
Section 25.1 GENERAL PRINCIPLES IN THE SALE OF SECURITIES
1/ THE PURPOSE OF OFFERINGS
The offering must be in line with this objective. The price of a security is equal to its present value, as long as all publicly available information has been priced in. This is the very basis of market efficiency. Conversely, asymmetric information is the main factor that can keep a company from selling an asset at its fair value.
Investors must therefore be given the information they need to make an investment decision. The company issuing securities and the bank(s) handling the offerings must provide investors with information. Depending on the type of offering, this can be in the form of:
- a mandatory legal written document called a prospectus, required by the exchange regulator (containing descriptive information: a reference document about the company, as well as a document detailing the transaction in question);
- presentations by management via meetings/conference calls with investors or electronic roadshows;
- valuations and comments by financial professionals on the deal and the issuer via notes by financial analysts and presentations to the bank’s sales teams, for example.
A firm underwriting commitment by the bank(s) handling the transaction can provide additional reassurance to investors, because if the bank is willing to arrange and underwrite the offering, it must believe that the offering will succeed and that the price is “fair”. After all, investors are also clients to whom the bank regularly offers shares.
Investor information needs and the complexity of the deal depend on the following:
- The amount of information that is already available on the issuing company itself. Clearly, an initial public offering of shares in a company unknown to the market will require a big effort to educate investors on the company’s strategy, business, financial profile and perhaps even the sector in which it operates. This information is already contained in the share price of a publicly traded company, as that price reflects investor anticipation. This is why it is generally easier to offer shares in a company that is already listed.
- Investor risk. Investors need more information for shares than for bonds, which are less risky.
- The type and number of investors targeted. In addition to regulatory restrictions, it is generally more difficult for a European company to sell its securities in the US than in Europe, especially if the company and its industry are not known outside its home country (sometimes the opposite can occur, as in the oil services sector, for example). Meanwhile, a private placement with a few investors is simpler than a public offering, market authorities imposing a lower level of information for transactions targeting only professional investors.
2/ THE ROLE OF BANKS
The bank(s) in charge of an offering have four roles, the complexity of which depends on the type of offering:
- Arranging the deal, i.e. choosing the type of offering on the basis of the goal sought: volume of securities to offer and in what form and timetable, choosing the market for the offering, contacts with market authorities, preparation of legal documents in liaison with specialised attorneys.
- Circulation of information: an offering is often an opportunity for an issuer to report on its recent activity, prospects and strategy. The consistency of this information is checked by the bank and the lawyers in charge of the deal during a phase called “due diligence”, which consists of interviews with the company’s management. Information is also gathered by the brokerage arm of the bank and then put out in research notes written by the bank’s financial analysts. The bank also organises meetings between the issuer and investors in one or more markets (roadshows or one-to-one meetings).
- Distribution of the paper: the bank’s sales teams approach their regular clients, the investors, to market the securities and take orders. The issue price is then set by the bank in liaison with the issuer or seller, and the securities are allocated to investors. An equilibrium price is established in the “after-market” phase. In the days after that, the bank may intervene in the market in order to facilitate exchanges of blocks among investors.
- Underwriting: in some cases the bank provides the issuer (or seller) with a guarantee that the securities will find buyers at the agreed price. The bank thus assumes a certain market risk. The magnitude of this risk will depend on the type of guarantee and on the timing of the commitment.
Most offerings, especially public offerings,1 require a syndicate made up of several banks. Depending on how involved it is in the deal, and in particular the degree of guarantee, any one bank may play the role of:
- global coordinator, who coordinates all aspects of an offering; the global coordinator is also lead manager and usually serves as lead and book-runner as well. For fixed-income issues, the global coordinator is called the arranger;
- the lead manager is responsible for preparing and executing the deal. The lead helps choose the syndicate. One (or more) leads also serve as book-runners. The lead also takes part in allocating the securities to investors;
- joint-leads play an important role, but do not usually serve as book-runners;
- co-leads may underwrite a portion of the securities but have no role in structuring the deal;
- co-managers play a more limited role in the transaction, normally just underwriting a small portion of securities. Sometimes co-managers will provide no underwriting commitment and have no placement role, they will merely associate their names with the transaction. This being called “check collecting”.
For some transactions (a block trade of already existing shares or a bond issue), the banks may buy the securities from the seller (or issuer) and then sell them to investors. This is called a bought deal. Unsold securities go onto the bank’s balance sheet.
A firm underwriting agreement carries less of a commitment than a bought deal. A firm underwriting is a commitment by the bank to buy the securities only if the offering fails to attract sufficient investor interest. In some cases, the bank may be released from its commitment in the event of force majeure like a market crash or a war declaration. A failure of the placement, not justified by a case of force majeure, is not a sufficient reason for the bank to withdraw.
Before agreeing to underwrite more complex deals, banks may wish to have some idea of investors’ intentions. They do so via a process called book-building, which occurs at the same time that information is sent out and the securities are marketed. Volumes and potentially prices from potential investors are listed in the book. This helps determine if the transaction is feasible and, if so, at what price. Only after the book-building process do banks choose whether or not to underwrite the deal. Book-building allows the banks running the transaction to limit significantly their risk, by assuring them that investors are willing to buy the securities.
In simpler transactions such as the placement of blocks or the issue of convertible bonds, the bank will almost always get feedback from a limited number of investors on their interest in the transaction and on the pricing. Market soundings are regulated by a European Directive (market abuse regulation, MAR).
In some cases, the bank does not pledge that the transaction will go through successfully, only that it will make its best efforts to ensure that this happens. This is rare in a formal documented offer, as investor confidence could be sapped if there is no formal pledge that the deal will go through. As a result, best efforts is the rule only in offerings by smaller companies or in very special cases (companies in financial distress, for example).
In some transactions, the bank’s commitment is halfway between an initial bought deal and a post-book-building bought deal. When a block of existing shares is being sold, a bank may make a “back-stop” or floor underwriting commitment, i.e. go through the book-building process but guarantee the seller a minimum price.
There are three techniques for adjusting the offering to investor actual behaviour during (or just after) the transaction: extension clause, greenshoe and clawback.
The extension clause allows shareholders wanting to sell shares or the company issuing new shares to sell more shares than initially planned if demand turns out to be strong. The option is disclosed in the prospectus and can be exercised at the time of the allocation. The size of the transaction can be increased by 15% in the case of a share issue and 25% in the case of a secondary placement.
To stabilise the price after the transaction, the issuer or seller may give the bank the option of buying a number of shares over and above the shares offered to investors (as many as 15% more in a capital increase and 25% more for block trades of existing shares). This is called a greenshoe (named after the first company to use it). The bank allocates all the securities to investors, including the greenshoe shares, i.e. more than the official offering. These additional shares are borrowed by the bank:
- If the price falls after the offering, the bank buys shares on the market up to the limit of the greenshoe. This supports the price. It then has 30 days to resell these shares if the price moves back up. If the price doesn’t rise, the bank repays the loan using the shares it bought to support the price. In this case the greenshoe is not exercised.
- If the price moves up, the bank can resell the shares or, if the price rises immediately after the transaction, the bank no longer has the shares so it will pay back the loan by exercising the greenshoe. The company will thus have sold more shares than originally planned.
Greenshoes are used for secondary offerings (i.e. sale of existing shares), new share issues (the lead bank receives, free of charge, warrants that it may or may not exercise) or convertible bond issues (when it takes the form of a simple extension of the issue, decided two or three days after its launch).
An offering targeted at several categories of investors (institutional, retail, employees, etc.) will be split into several tranches reserved for each of them. The clawback clause gives the company some flexibility in the size of each tranche. Hence, if institutional demand is very heavy and retail demand very light, the clawback allows the shares initially allocated to retail investors to be reallocated to institutional investors.
If a large shareholder sells part of his shares through the transaction, the placement will be eased if this shareholder commits not to sell additional shares over a certain period of time (unless the bank coordinating the transaction gives the green light). This is called a lock up and lasts between a few months and a year.
To simplify the transaction, the bank may advise the company to target a limited number of investors, thus avoiding the rules governing a public offering, including supervision by market authorities, obligation to present information, etc. This is called a private placement and is possible on all types of products. Private placements are in particular often used in offerings to US investors (generally under rule 144A), as the offering would otherwise be subject to extremely strict restrictions. They are also used in Europe for some bond placements.
3/ ISSUE DISCOUNTS
Studies show that when a company is floated, its stock often rises by an average of about 10–15% over its issue price, depending on the country, the timing and how the rise is calculated. Meanwhile, shares in a company that is already listed are usually offered at a discount ranging from 2–5%, although the range varies profoundly according to different countries.
This discount is theoretically due to the asymmetry of information between the seller and the investors or intermediaries. One side knows more about the company’s prospects, while the other side knows more about market demand. The transaction is therefore possible. It’s all a matter of price! Selling securities generally sends out a negative signal, so the seller has to price his securities slightly below their true value to ensure the deal goes through and that investors are satisfied.
The IPO discount could be due to the fact that there are both informed and uninformed investors. Uninformed investors cannot distinguish which issues are really attractive and thus are exposed to the winner’s curse. This is why an average discount is offered, to guarantee an appropriate return for uninformed investors who will be receiving many shares of a “bad deal” and few shares of a “good deal”. Others suggest that the discount is a way of remunerating the banks underwriting the deal. The discount makes the issue easier to market, reduces risk and allows them to meet institutional client demand.
The issue discount is another way to persuade investors to invest in a transaction that appears to carry some risk.
For bonds, the investor will generally get a slightly better yield to maturity (5 to 20 basis points) on a new issue than on the secondary market of an existing issue with similar conditions. This premium will be called the new issue premium (NIP), a premium in rate being equivalent to a discount in price.
So much for the major principles. Let’s now look at how the main types of securities are offered. As you will see, the methods converge towards two main techniques: bought deals and book-building.
Section 25.2 INITIAL PUBLIC OFFERINGS
The purpose of this section is not to analyse the motivations, strategic or otherwise, of an IPO (that will be seen in Chapter 44) but simply to describe how it works.
1/ HOW AN IPO WORKS
IPOs are surely the most complex of transactions, taking many months to put in place. They involve selling securities, about which prior information is extremely limited, to a large number of investors, including institutional and retail investors and employees.
An IPO can include a primary tranche (i.e. shares newly issued by the company) and/or a secondary tranche (i.e. disposal of existing shares by an existing shareholder). The techniques are the same for both tranches and, in fact, existing shares and new shares are bundled up in the same lot of shares to be offered. They are fungible.
However, the techniques vary depending on whether the shares are being offered to institutional investors, retail investors or employees.
2/ HOW IPOS ARE MADE
A number of techniques exist for floating a company. However, in the past few years, IPOs on regulated markets have almost all been in the same form: that of an underwritten deal with institutional investors and a retail public offering with retail investors.
(a) Book-building
Offerings of securities to institutional investors are most often implemented through a book-building. This is the main tranche in almost all IPOs. Under this system, one or more banks organise the marketing and sale of securities to investors via a phase of book-building. The price set after book-building will serve as a basis for setting the price of the retail public offering. Other techniques are used for the other tranches (employees and retail investors, in particular).
The initial review phase is handled by the banks. This consists of assessing and preparing the legal and regulatory framework of the deal (choice of market for listing, whether to offer shares in the US, etc.); structuring the deal; supervising documentation (due diligence, prospectus) and underwriting and execution agreements; preparing financial analysis reports; designing a marketing campaign (i.e. the type and content of management presentations, programme of meetings between management and investors).
Then comes the execution phase, with the publishing of financial analysis notes by syndicate banks. This is a pre-marketing period lasting one to two weeks prior to the effective launch of the operation. The notes are presented to investors during “warm-up” meetings, which help test investor sentiment. Analysts’ research notes cannot be published during the blackout period that precedes the launch. The terms of the transaction, particularly the price range or maximum price, are set on the basis of conclusions from this pre-marketing exercise.
The marketing campaign itself then begins, and the offering is under way. During this period, full information is distributed via draft prospectuses (certified by market authorities), which may be national or international in scope. The prospectus includes all information on the company and the transaction. The offering is marketed within a price range of about 15% or with a maximum price. Company managers are mobilised during this period for numerous meetings with investors (roadshows) or for one-on-one meetings. The information given to investors is mainly on company results, markets and strategy.
In the meantime, investor intentions to subscribe in terms of volumes and prices are recorded in an order book, on the basis of the preliminary price range.
After this period, which can last 5–15 days, the sale price of the existing shares and/or newly issued shares is set. The price reflects market conditions, overall demand as reflected in the order book and the price sensitivity that investors may have expressed.
Not until after this phase might banks enter into a firm underwriting agreement. The shares are then immediately allocated, thus limiting the bank’s risk. After allocation, investors are theoretically committed. However, up to the actual settlement and delivery of the shares (three days after the transaction), banks still face counterparty risk. There is also business risk in the form of an institutional investor who decides not to take delivery of the shares after all (an agreement is normally found between the bank and the investor). In sum, the only risks the syndicate takes is that of a market crash between the moment the price is set and the moment when the shares are allocated, and that of stabilising the price for around a month after the transaction by buying shares on the market.
The guarantee given by the bank to the company is also implicitly a comforter for the market. The bank determines a value after review of internal information. This partly resolves the problem of asymmetry of information. The signal is no longer negative, because a bank with access to internal information is taking the risk of buying the shares at a set price if the market does not.
A standardised press release (with the issue price) is sent out after the price is set and the subscription period is closed. The lead bank knows the quantity and quality of demand. The book-runner allocates the new shares to investors in concert with the issuer and/or seller, who can thus “choose” its shareholders to a certain extent.
The shares are allocated on the basis of certain criteria determined in advance. Allocation is discretionary but not arbitrary. The goal may be to favour US, European or local investors. Generally, the main goal in allocation is to have a balance between investors with different investment timing in order to ensure a stable aftermarket. The banks may steer the issuer to what it believes are quality investors, thus limiting excessive flowback, i.e. the massive sale of securities immediately after the offering.
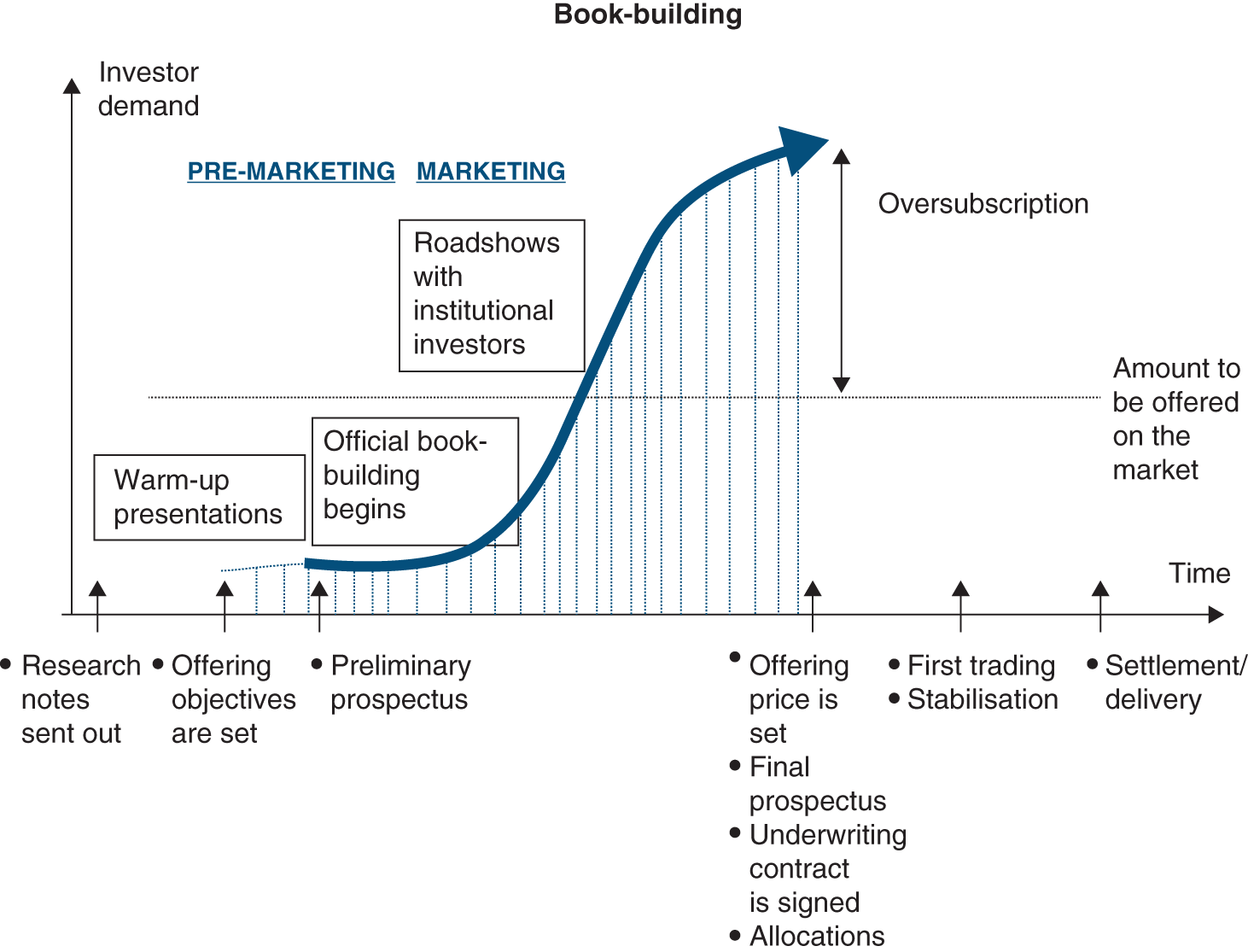
Book-building offers several advantages, including greater flexibility. For one thing, the price can be adjusted as necessary during the marketing phase, which can sometimes last several weeks. Moreover, shareholders can still be chosen via discretionary allocation of shares.
(b) How shares are offered to retail investors
In an underwritten deal, shares are allocated at the discretion of the lead, based on the order book, as well as on criteria announced in advance. However, when shares are being sold to retail investors, the issue is centralised by the market itself.
- The retail public offering
In a retail public offering, a price range is set before the offering, but the exact price is set after the offering. The final price reflects market demand. French market authorities, for example, require a marketing period lasting at least three days, after which a draft prospectus is issued with the characteristics of the deal. Based on a price range, financial intermediaries collect orders from investors. The issue price is set jointly by the issuer and the syndicate lead, and is generally equal to the underwriting price.2 The final prospectus is then approved by the market authorities.
With the agreement of the market authorities, the banks can adjust the price if they have previously reserved the right to do so but, in general, they must begin the process anew if the new price is outside of the initial range. Shares are allocated on the basis of orders if supply is equivalent to demand and can be reduced on the basis of predetermined criteria. Allocation of shares to the various categories of buyers is done on the same basis as the fixed-price offer.
Normally, at least 1% of the order is filled, but there may be provision for a minimum number of shares per order, so that broker fees do not end up swallowing any potential gain. Similarly, there are sometimes several categories of orders with different allocation priorities.
- Fixed-price offering
Under a fixed-price offering, a certain number of shares are offered to the public at a pre-set price, which is generally identical to the price offered to institutional investors. The price is set after the book-building phase and is independent of market conditions. It is applied regardless of the number of shares requested. If it is far below what the market is willing to pay, the price will rise sharply in the days after the IPO and primary market buyers will have a capital gain to show for their initiative.
The only difference between a fixed-price offering and a retail public offering is how the price is set.
- Minimum-price offering
Under this technique, a number of shares are offered to the public at a certain price, under which they will not be sold. The local stock exchange centralises orders, in which buyers must specify a floor price, and tries to find a sufficiently wide price range at which orders can be allocated in a certain proportion (about 6%) if there is sufficient demand.
In a minimum-price offering, some orders may be shut out entirely, and orders at very high prices are paradoxically eliminated. This explains why the first quoted price is above the pre-set minimum price. If demand is too strong to quote the shares, trading is declared “limit up” and resumes at a higher price, or another technique is used for the initial quotation.
- An ordinary full listing
The principle of an ordinary full listing is simple: the shares are offered on the basis of the market’s normal trading and quoting conditions. A minimum sale price is set, but buy orders are not centralised by the local stock exchange. Quotation is possible at a price normally no higher than 110% of the minimum price; at least 6% of the buy orders are filled (4% in exceptional cases). As in a minimum-price offering, trading may be suspended “limit up” and resumed at a higher price. In addition, orders may have to be covered by sufficient funds (the goal being to discourage speculation).
3/ US LISTINGS FOR NON-US COMPANIES
Companies normally list their shares on their domestic stock market, where they are better known. However, they may wish to tap foreign investors to widen their shareholder base and could thus seek a foreign listing.
This decision is not so unusual – over 3,000 foreign companies are listed in the US!
Since the American markets (NYSE and Nasdaq) are traditionally the preferred alternative for companies wanting to list, we focus our attention on US listing.
(a) Private placements
Under rule 144A, companies may opt for private placement of their shares, but they may only do so with US qualified institutional buyers (QIBs). QIBs are then prohibited from selling their shares on the open market for two years, but can trade with other QIBs via the PORTAL system. Private placements are simply a means of gaining access to US investors, but do not allow a company to register its shares with the Securities and Exchange Commission (SEC, the US market regulator) or to quote them in the US.
This is the least restrictive way to raise capital on US markets, as private placements are not registered with the SEC and come under the 12g3-2(b) waiver. All the issuing company has to do is translate the information that it has provided to its domestic market.
(b) Indirect listing via ADR
ADRs, also known as DRs or GDRs,3 are negotiable instruments issued by a US bank and representing the shares that it has acquired in a foreign company listed on a non-US market – something like tracking stocks, except they are not issued by the company itself. ADRs are traded on a regulated market (Nasdaq or NYSE) or an over-the-counter (OTC) market.
The ADR shares can be established either for existing shares already trading in the secondary market of the home country, or as part of a global offering of new shares.
There are three types of ADR depending on whether the company wishes to be listed on an organised market and raise funds in the US. The disclosure requirements will be more or less onerous depending on the type of ADR.
Nearly 3,000 ADRs are listed from 90 countries, including Sanofi, Telefónica, Korea Electric Power, ArcelorMittal, BP, Alibaba, JD.com, Teva and many others.
(c) Full listing
Companies can also list their ordinary shares in both their home countries and directly in the US. This gives them access to institutional investors whose by-laws do not allow them to buy shares outside the US.
The main difference between ordinary registered shares and ADRs is that ordinary registered shares carry lower transaction costs as there is no depositary. They are also more liquid and less subject to arbitrage trading between domestic shares and ADRs.
Full listing is a relatively long and complex process suitable only for very large companies (UBS, Deutsche Telekom, Repsol YPF, etc.).
Section 25.3 ICOS
An ICO, or initial coin offering, is a fund-raising process for a start-up, frequently in the technology sector and linked to blockchain cryptography. The name is derived from IPO (initial public offering) for marketing purposes, and is similar only in name as it differs quite significantly from the IPO process. To avoid scams, of which there were many during the initial ICO buzz of 2017/2018, market authorities have actively implemented regulations to govern the ICO process.
Start-ups seeking to raise capital will provide in exchange not shares but “tokens”, issued with blockchain technology, which can then be traded on specialised platforms. There are several categories of tokens:
- Utility tokens (the most widespread today) that will give access to a good or service in development by the company raising the funds.
- Security tokens that resemble financial securities in that they give access to all or part of the company’s income and/or dividends.
- Community tokens (the first to appear) that give their holders the opportunity to participate in the governance of the project financed by the company.
- Asset tokens that represent rights over underlying assets.
A company wishing to carry out an ICO presents its project and the characteristics of its tokens in a document entitled a “white paper” (the equivalent of the prospectus for an IPO). One of the difficulties with ICOs is the valuation of the token. Depending on the characteristics of the token, its value will depend more on the use that will be made of it, or on the income derived from this use.
Section 25.4 CAPITAL INCREASES
A financial approach to capital increases is developed in Chapter 38.
1/ THE DIFFERENT METHODS
The method chosen for a capital increase depends:
- on whether or not the company is listed;
- on how willing current shareholders are to subscribe.
(a) Listed companies
When the large majority of current shareholders are expected to subscribe to the capital increase and it is not particularly necessary or desirable to bring in new shareholders, the transaction comes with pre-emptive subscription rights (the transaction is then called a rights issue). The issue price of the new shares is set and announced in advance and the offering then unfolds over several days. The price is set at a significant discount to the market price, so that the transaction will go through even if the share price drops in the run up to the listing of new shares. To avoid penalising existing shareholders, the issue comes with pre-emptive subscription rights, which are negotiable throughout the transaction period.
However, when current shareholders are not expected to subscribe or when the company wants to widen its shareholder base, there is no issue of pre-emptive subscription rights. The issue price is then not set until a marketing and pre-placement period has been completed, with a very slight discount to the share price at the end of this period. There are no pre-emptive subscription rights, but there may be a period during which current shareholders are given priority in subscribing.
(b) Unlisted companies
In this case, the issue price’s discount will not be dictated by the fear that the share price will fluctuate during the operation (as the company is not listed), but rather by the wish of current shareholders to raise cash by selling the subscription rights they may have received.
If current shareholders do not wish to raise cash, then the company will issue pre-emptive subscription rights at a price about equal to the share price, or may issue shares to identified investors that have been found via a private placement.4
WHICH METHOD SHOULD BE USED FOR A CAPITAL INCREASE?
| Rights issue subscribed to mainly by: | Listed company | Unlisted company |
|---|---|---|
| Current shareholders | Pre-emptive subscription rights Steep discount to the market price | Pre-emptive subscription rights with a steep discount if current shareholders wish to raise cash Pre-emptive subscription rights with no discount or no pre-emptive rights if current shareholders do not want to raise cash |
| New shareholders | Offer without pre-emptive subscription rights (at a slight discount to the current share price) In some cases, a reserved rights issue | Pre-emptive subscription rights with a steep discount if shareholders want to raise cash Reserved rights issue if shareholders do not want cash |
Shares cannot be issued below par value (this is also the case for listed companies). If the share price is below par value, the par value could be reduced by offsetting it against past losses.
2/ RIGHTS ISSUE
A fixed-price rights issue with pre-emptive subscription rights (also called privileged subscription or rights issues) is the traditional issue preferred by small investors (or their representatives). Such issues acknowledge their loyalty or, conversely, allow them to raise a little cash by selling their subscription rights.
In some countries, such as the US and Japan, rights issues are quite rare, while in Continental Europe they generally have to be sold by rights.
Such issues remain open for at least 10 trading days. Banks underwrite them at a price well below the current share price, generally at a discount of 15–30%, but up to 30–50% when a financial crisis increases the volatility of stocks. No bank will guarantee a price near the current market price, because the longer the subscription period, the greater the risk of a drop in price. It is at this price that the banks will buy up any shares that have not found takers.
A steep discount would be a considerable injustice to existing shareholders, as the new shareholders could buy shares at 20% below the current market price. Rights issues resolve this problem by allowing existing shareholders to buy a number of shares proportional to the number they already have. If existing shareholders use all their pre-emptive rights, i.e. buy the same proportion of new shares as they possess of existing shares, they should not care what price the new shares are offered at.
Even when existing shareholders do not wish to subscribe, the pre-emptive subscription rights keep them from being penalised, as they can sell the right on the first day it is detached.
(a) Definition
The subscription right offers the existing shareholder:
- the certainty of being able to take part in the capital increase in proportion with their current stake;
- the option of selling the right (which is listed separately for listed companies) throughout the operation. This negotiable right adjusts the issue price to the current share price.
The subscriber may, thanks to their subscription rights, subscribe unconditionally to an amount equivalent to the pro rata of their holdings in the company. Should they wish to subscribe in a greater quantity, they may do so conditionally, provided that other shareholders do not take up their own rights to the subscription. Otherwise, should they seek certainty with regard to their intentions, they will have to purchase the subscription rights from shareholders who do not wish to participate.
The subscription right is similar to a call option whose underlying asset is the share, whose strike price is the issue price of the new shares and whose exercise period is that of the capital increase. Hence, its theoretical value is similar to that of a call option whose time value is very low, given its short maturity.
If the issue price and the current share price are the same, the subscription right’s market value will be zero and its only value will be the priority it grants.
If the share price falls below the issue price, the rights issue will fail, as nobody will buy a share at more than its market price. The right then loses all value. Fortunately, the reverse occurs more frequently.
(b) Calculating the theoretical value of the subscription right
Let’s take a company that has 1,000,000 shares outstanding, trading at €50 each. The company issues 100,000 new shares at €40 each, or one new share for each 10 existing ones. Each existing share will have one subscription right, and to buy a new share for €40, 10 subscription rights and €40 will be required.
After the new shares have been issued, an existing shareholder who holds one share and has sold his pre-emptive subscription rights must be in the same situation as an investor who has bought 10 pre-emptive subscription rights and one new share. So the share price after the deal should be equal to:
but also:
In our example:
Hence:
The post-deal share price should be equal to:
It is easy to calculate the theoretical value of the subscription right:
where V is the pre-issue share price, E the issue price of the new shares, N′ the number of new shares issued and N the number of existing shares.
We can see that this formula can be used to find the previous result.
The detachment of subscription rights is conceptually similar to a bonus share award. Hence, the existing shareholder may, if they wish, sell some pre-emptive rights and use the cash and remaining rights to subscribe to new shares, without laying out new cash (see the exercise at the end of this chapter).
(c) Advantages and drawbacks of pre-emptive rights
The subscription right is valid for at least 10 trading days – a relatively lengthy amount of time. The issue price therefore has to be well below the share price, so that if the share price does fall during the period, the deal can still go through. In such case, the value of the right (i.e. the difference between the share price and the issue price) will fall but will remain positive, as long as the share price, ex-rights, is above the issue price.
This is a double-edged sword as, once the deal is launched and the rights issued, nothing can delay the capital increase, even if the share price drops significantly during the deal. This is why the initial discount is so significant.
Complicating the transaction further is the fact that shareholders who do not possess a number of shares divisible by the subscription parity must sell or buy rights on the market so that they do. This can be difficult to do on international markets.
Another potential complication is the large proportion of US investors among current shareholders who are sometimes unable to exercise their pre-emptive subscription rights as some are not authorised to invest in options, which subscription rights are.
3/ ISSUE OF SHARES WITHOUT PRE-EMPTIVE SUBSCRIPTION RIGHTS
In issues of shares without subscription rights, the company also turns to a bank or a banking syndicate for the issue. But their role is more important in this case, as they must market the new shares to new investors. They generally underwrite the issue, as described above for IPOs. A retail public offering can be undertaken simultaneously. Alternatively, the bank can simply launch the transaction and centralise the orders without having gone through a book-building phase. The company may issue 10–15% more shares than expected, via a greenshoe, under which warrants are issued to the banks (see 25.1, 2/).
Local regulations tend to limit the flexibility to issue shares without subscription rights, so that the shareholder will not be diluted at an absurdly low price. Therefore, in most countries, regulation fixes a maximum discount to the last price or a minimum issue price as a reference to a price average.
When new shares are issued with no pre-set price, current shareholders can be given first priority without necessarily receiving pre-emptive rights. Indeed, such a priority period is the rule when pre-emptive rights are not issued. However, priority periods have the disadvantage of lengthening the total transaction period, as they generally last a few trading days (this is the minimum amount of time to allow individual shareholders the time to subscribe).
Legally speaking, a public issue of new shares, with or without pre-emptive rights, is considered to have been completed when the banks have signed a contract on a firm underwriting the transaction, regardless of whether or not the shares end up being fully subscribed.
Such issues of shares can be implemented in the form of a private placement to qualified investors (usually for a minor portion of capital).
4/ EQUITY LINES
The way an equity line works is that a company issues warrants to a bank that exercises them at the request of the company when it needs to raise equity. Equity lines smooth the impact of a capital increase over time. The shares issued when the warrants are exercised are immediately resold by the bank.
Equity lines are suitable for young businesses where the stock performance history does not allow conventional rights issues. However, it opens the way to many uncertainties, particularly on the terms imposed on the banks in exercising warrants and reselling the shares.
5/ RESERVED CAPITAL INCREASE
The placement of securities is infinitely simplified if the capital increase is reserved for a single identified investor. The challenge is then simply to reassure shareholders about the fairness of the issue price of the securities, as the reserved capital increase must be voted on at an EGM with, of course, cancellation of preferential subscription rights.
6/ EMPLOYEE STOCK OWNERSHIP PLANS
Employee Stock Ownership Plans (ESOPs) enable employees to acquire shares in the company they work for via a share placement process. The placement of securities is made directly with employees, generally at the same time as the payment of profit-sharing and incentive schemes, which makes it possible to finance all or part of the subscription. The company may also offer more structured share subscription mechanisms (downside protection of the share, upside multiplier).
Section 25.5 BLOCK TRADES OF SHARES
A block is a large number of shares that a shareholder wishes to sell on the market. Normally, only a small fraction of a company’s shares are traded during the course of a normal day. Hence, a shareholder who wants to sell, for example, 5% of a company’s shares cannot do so directly on the market. If he did, he could only do so over a long period and with the risk of driving down the share price. Blocks are sold via book-building and/or bought deals, which were described above.
1/ BOOK-BUILDING AND ACCELERATED BOOK-BUILDING
Like a rights issue or an IPO, a block trade can be done via book-building. However, block trades are “simpler” deals than capital increases or IPOs, the company is already known to the investors as already public and the amount to be placed is smaller. Hence block trades require less marketing. Book-building is faster, top management is less involved or not involved at all, and the deal can sometimes be done within a few hours.
Bigger transactions involving a strategic shift (exit by a controlling shareholder, etc.) may require an intense marketing campaign, and the deal will be managed as if it were a rights issue.
Book-building can come with a public offer of sale when the company wants to allow retail investors to acquire shares, but only for the larger issues. Barring a waiver from Euronext, a retail offering is possible only if it involves at least 10% of the total outstanding shares or at least 20 times the average daily volumes during the previous six months.
Block trades use techniques that are similar to those of IPOs. For example, prices can be set in advance or on the basis of terms set when the offering begins. However, in the latter case, no price range is required (but the price-setting mechanism and the maximum price must be spelled out). In the requisite filings with Euronext, the initiator can reserve the right to withdraw the offer if take-up is insufficient or increase the number of shares on offer by as much as 25% if demand is greater than expected.
2/ BOUGHT DEALS AND BACK-STOPS
When the seller initiates book-building or accelerated book-building, he has no guarantee that the transaction will go through. Nor does he know at what price the deal will be done. To solve this problem, he can ask the bank to buy the shares itself. The bank will then sell them to investors. This is called a “bought deal”.
The bank is then taking a significant risk and will only buy the shares at a discount to the market price. In recent bought deals involving liquid stocks, this discount ranges from 2% to 5%; it was between 10% and 20% mid-2009.
The way it works is this: the seller contacts a few banks one late afternoon after the markets close. They may have mentioned to some banks a few days or weeks beforehand that they might be selling shares, thus ensuring better-quality replies. The seller asks each bank the price it is willing to offer for the shares. Bids must be submitted within a few hours. The seller chooses the bank solely on the basis of price, and the shares are sold that very night. The bank must then organise its sales teams to resell the shares during the night in North America or Asia, taking advantage of the time difference, and then the following morning in Europe.
For the seller, bought deals offer the advantage of being certain that the deal will go through and at the price stated at the moment when it decides whether to sell. There are some disadvantages, however:
- the deal will generally be at a greater discount than in accelerated book-building;
- share performance can suffer, as the bank that has acquired the shares will want to sell them as quickly as possible, even if that means making the price fall.
In a very hot market, the seller may have the best of both worlds in transactions with a back-stop.
- The bank sets up an order book so that the firm can benefit from an increase in share price.
- The bank guarantees a minimum price. If all or part of the placement cannot be made at that price, the bank will buy the shares at the back-stop price.
Banks can be very aggressive when seeking to gain the right to execute such transactions in order to build credentials and comfort their ranking in league tables. A number of large transactions (in particular when governments are sellers) have led to heavy losses for investment banks in charge, leading some banks to leave this market altogether, deemed too risky.
Section 25.6 BONDS
As the bond market develops and becomes more international, investors need benchmarks to measure the risk of default by issuers they do not always know very well. Ratings have thus become crucial in bond offerings. The market for companies that do not have a rating from at least one agency is more complex to tap, as it can be closed from time to time (the market for unrated issuers was also closed for several weeks during the Covid-19 crisis). For an offering in the US, the issuer will need to have at least two ratings.
As we mentioned in Chapter 20, the corporate bond market can be separated between companies having a rating of at least BBB (investment grade) and companies rated BB or lower (below investment grade). When they want to issue bonds, the latter must offer higher interest rates. Such bonds are called “high yield”. The investment grade and high yield markets are separate, not just for the issuers, but also for investors and for the investment banks handling the offering. It should be noted, however, that depending on the situation, some issuers rated BB+ or even BB (known as crossovers) may issue with investment grade type documentation.
1/ INVESTMENT GRADE BONDS
The euro switchover naturally gave rise to a pan-European bond market, and has allowed much larger issues than were previously possible on national markets. €1bn issues are no longer rare, and only issues of €10bn or more are exceptional.
Bond offering techniques have thus evolved towards those used for shares, and market regulations have followed suit. For example, competitive bidding has gradually given way to book-building. Competitive bidding consists of a tender from banks. The issuer chooses the establishment that will head up the offering on the basis of the terms offered (mainly price). It thus takes the risk of giving the lead mandate to a bank that is overly aggressive on price. The reason this is risky is that prices of bonds on the secondary market may fall after the operation begins. Buyers will not like this. Competitive bidding is similar to a bought deal and is often used by state-owned companies.
Other placement techniques exist (but they are usually used by sovereign issuers): Dutch auctions (“reverse auctions”) are one example.
Book-building helps avoid price weakness after launch, as the issue price (or spread) is not pre-set. The lead bank suggests a price range and sounds out investors to see what price they are willing to pay. Presentations to investors, one-on-one meetings and electronic roadshows over the Internet or Bloomberg allow management to present its strategy.
The lead then builds a book of volumes and prices (either rate or spread) offered by each investor interested in the issue. There is little risk of miscalculation, as the issue price is set by the market. The period between when the price is set and the effective delivery of the shares is called the grey market (this is also the case for IPOs and rights issues). Bonds are traded on the grey market without, technically, even existing. Transactions on the grey market are unwound after settlement and delivery and the first official quotations. The lead intervenes on the grey market to maintain the spread at which the issue has been priced.
So there are some similarities between share and bond offerings. However, the process is much shorter for bonds and can be extremely short, especially if a company is an investment grade frequent issuer, and if the issue is on its local market. In such case, the placement will be implemented in a few hours with no marketing efforts. The process is longer for a first issue or if the company is targeting a large proportion of international investors.
The role of the lead is not just to market the paper, but to advise the client, where applicable, in the obtaining of a rating. It determines the spread possible through comparisons with issuers having a similar profile and chooses the members of the syndicate to help sell the bonds to the largest number possible of investors.
When the company plans several issues in the medium term, it can put out an umbrella prospectus to cover all of them, under an issue of EMTNs (euro medium-term notes). This allows the company to tap the markets very rapidly when it needs to, or when the market is attractive, at least to qualified investors, as issues to individual investors are much more cumbersome in terms of documentation.
2/ HIGH YIELD BONDS
By definition, high yield or non-investment grade bonds are risky products. High yield issues take longer and require more aggressive marketing than a standard issue, as there are fewer potential buyers.
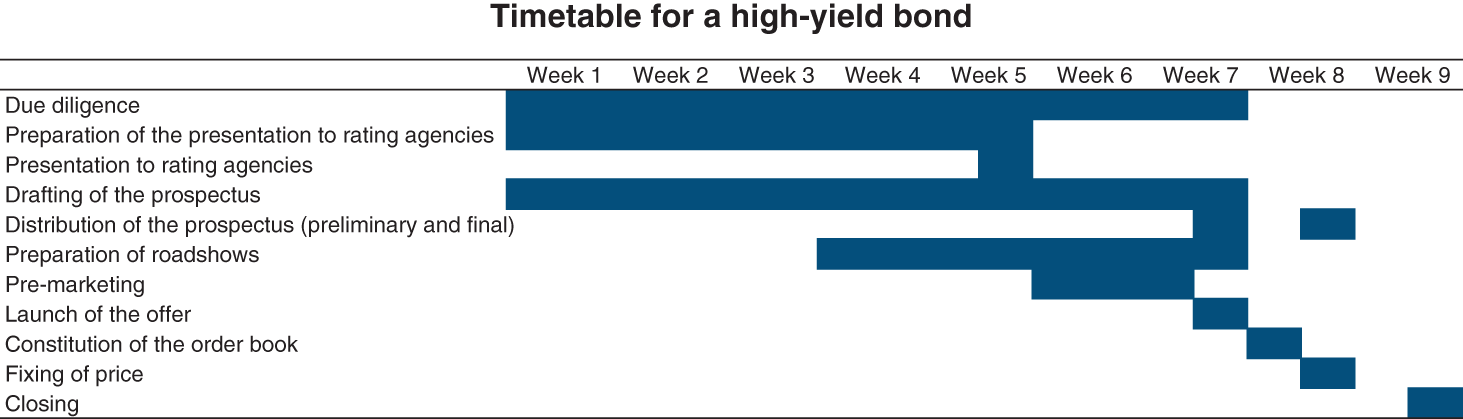
3/ PRIVATE PLACEMENT
As explained previously, private placements are an alternative to regular bond issues and allow issues of smaller amounts.
Placement techniques for private placements are much closer to placements of syndicated loans (see Section 25.8) than to standard bond issues. Investors are generally contacted in anticipation of the transaction to gauge their appetite for the transaction and the type of issuer that they could consider. The transaction is then proposed to firms that meet the criteria defined by the investors. Investors are typically insurance companies or pension funds looking for long-term investment and not caring much about the liquidity of their investment.
The placement requires the drafting of a prospectus as in a standard transaction.
Obviously, each local market (US, European, Schuldschein in Germany) has its specificities. Signs of a structuring market, standard issue contracts are now available for European private placements.
Section 25.7 CONVERTIBLE AND EXCHANGEABLE BONDS
Convertible bonds (CBs) (examined in Section 24.2) are a very specific product. From a placement point of view, the investor of a convertible bond will benefit from all the information given by the firm to the equity market. In addition, the share price allows the investor to value precisely the option part of the instrument that he will buy.
The only factor that could make an investor hesitate to invest in a convertible bond is the product’s complexity. However, CBs are now well known to professional investors, and are sold mainly to specialised investors or hedge funds.
Section 25.8 SYNDICATED LOANS
Syndicated loans are not securities in their own right, but merely loans made to companies by several banks.
A syndicated loan offering is nonetheless similar to a bond issue. The company first receives a proposal from different banks to put in place or (refinance) a syndicated loan. On the basis of these proposals, the firm will retain one (or several) bank(s) that will arrange the transaction (the mandated lead arrangers, or MLAs). MLAs also usually have the role of bookrunners. This bank may do a bought deal of the entire loan and then syndicate it afterwards. The arranger is paid specifically for its advisory and placement role. When a large number of MLAs are retained, some will have a specific role to coordinate the transaction and facilitate the negotiation of the documentation (they are the facilitators, coordinators or agents of the documentation).
The main terms are negotiated between the documentation agent and the company and are put into a term sheet. Meanwhile, the bank and company choose a syndication strategy along with the banks (or financial institutions) that will be members of the syndicate.
After meetings with the company and a memorandum of information is drawn up (which can be avoided if the company is public), the banks contacted will decide whether or not to take part in the syndicated loan. Once the syndicate is formed, the legal documentation is finalised.
The entire process can take two months between the choice of arranger and the release of funds.
Syndicated loans are closely dependent on the quality of the company’s relationship with its banks. Syndicated loans do not often make much money for the banks, and they take part only as they wish to develop or maintain good relations with a client, to whom they can later market more lucrative transactions (called “side business”). Membership of a syndicate sometimes even comes with the stipulation that it will be remunerated through an implicit or explicit pledge from the company to choose the bank as the lead on its next market transaction or as an advisor on its next M&A deal.
SUMMARY
QUESTIONS
EXERCISES
ANSWERS
BIBLIOGRAPHY
NOTES
- 1 That is, for a flotation on a regulated market or a public retail offer.
- 2 Retail investors are generally offered a discount or are exempt from certain fees.
- 3 American depositary receipts may also be called – generically – depositary receipts (DRs), or Rule 144A depositary receipts or global depositary receipts (GDRs), which are the “private placement” discussed in the text. However, different names typically identify the market in which the depositary receipts are available: ADRs are publicly available to US investors on a national stock exchange or in the OTC market; Rule 144A ADRs are privately placed and resold only to QIBs in the US QIB PORTAL market; GDRs are generally available in one or more markets outside the foreign company’s home country, although these may also be known as ADRs.
- 4 In the rare case of a capital increase with no subscription rights and not reserved for identified investors, the price is based on an expert appraisal or is set at book value.

