Test14 | Hàm logarit
Cho $f(x)=\log_2 x$. Ta có $f(2)=$
- A. 2
- B. 1
- C. 0
Cho $f(x)=\log_2 x$. Ta có $f(-2)=$
- A. 2
- B. 1
- C. 0
- D. ko tính dc
Cho $f(x)=\log_2 x$. Ta có $f(0)=$
- A. 2
- B. 1
- C. 0
- D. ko tính dc
Cho $f(x)=\log_2 x$. Ta có $f(1)=$
- A. 2
- B. 1
- C. 0
- D. ko tính dc
Cho $f(x)=\log_2 x$. Ta có $f'(x)=$
- A. $\frac{1}{x.\ln a}$
- B. $\frac{1}{x}$
- C. $\frac{1}{x.\ln x}$
Cho $f(x)=\ln x$. Ta có $f'(x)=$
- A. $\frac{1}{x.\ln a}$
- B. $\frac{1}{x}$
- C. $\frac{1}{x.\ln x}$
Cho $f(x)=\log x$. Ta có $f'(x)=$
- A. $\frac{1}{x.\ln 10}$
- B. $\frac{1}{x}$
- C. $\frac{1}{x.\ln x}$
- D. $\left ( \log_{10}x \right )’$
A, D
Cho $f(x)=\lg x$. Ta có $f'(x)=$
- A. $\frac{1}{x.\ln 10}$
- B. $\frac{1}{x}$
- C. $\frac{1}{x.\ln x}$
- D. $\left ( \log_{10}x \right )’$
A, D
Cho $f(x)=\log_2(x^3+x^2)$. Ta có $f'(x)=$
- A. $\frac{1}{x^3+x^2}$
- B. $\frac{1}{(x^3+x^2).\ln 2}$
- C. $\frac{1}{(x^3+x^2).\ln 2}.\left ( x^3+x^2 \right )’$
- D. $\frac{1}{(x^3+x^2).\ln 2}.\left ( 3x^2+2x \right )$
- E. $\frac{3x^2+2x}{(x^3+x^2).\ln 2}$
C, D, E
Cho $f(x)=\ln(x^3+x^2+1)$. Ta có $f'(x)=$
- A. $\frac{1}{x^3+x^2+1}$
- B. $\frac{3x^2+2x}{(x^3+x^2+1)}$
- C. $\frac{3x^2+2x+1}{(x^3+x^2+1)}$
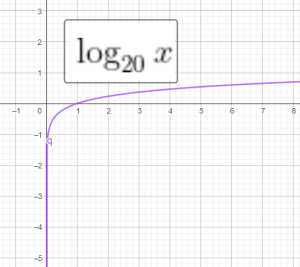
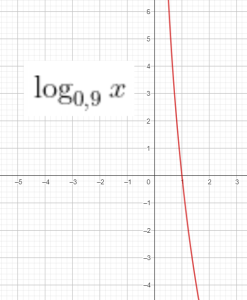
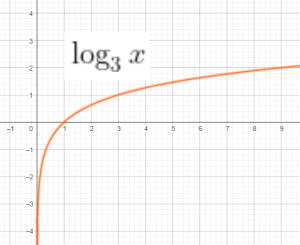
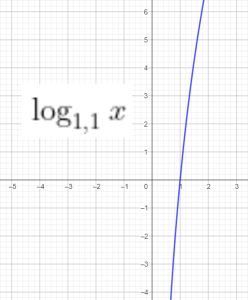
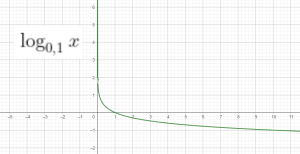
Các hàm số giảm là
- A. $\log_{20}x$
- B. $\log_{3}x$
- C. $\log_{1,1}x$
- D. $\log_{0,9}x$
- E. $\log_{0,1}x$
D, E
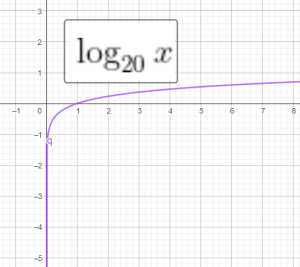

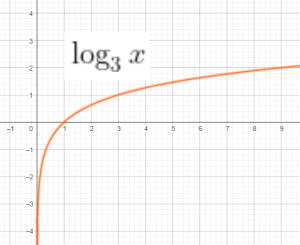


Các hàm số tăng là
- A. $\log_{20}x$
- B. $\log_{3}x$
- C. $\log_{1,1}x$
- D. $\log_{0,9}x$
- E. $\log_{0,1}x$
A, B, C
Khi $a>1$ thì $f(x)=\log_a x$
- A. đồng biến
- B. nghịch biến
Khi $0<a<1$ thì $f(x)=\log_a x$
- A. đồng biến
- B. nghịch biến
Khi $0<a<1$ thì $f(x)=\log_a x$ có $f'(x)$
- A. dương
- B. âm
Khi $a>1$ thì $f(x)=\log_a x$ có $f'(x)$
- A. dương
- B. âm
Đồ thị của hàm $f(x)=\log_a x$ có đường tiệm cận
- A. đứng
- B. ngang
Đồ thị của hàm $f(x)=\log_a x$ có đường tiệm cận là
- A. $x=0$
- B. $y=0$
