Test38 | Phương trình mặt phẳng
Mặt phẳng đi qua điểm $M(1;2;3)$ và có vector pháp tuyến $\overrightarrow{n}(4;5;6)$ thì có phương trình là:
- A. $4(x-1)+5(y-2)+6(z-3)=0$
- B. $1(x-4)+2(y-5)+3(z-6)=0$
Mặt phẳng đi qua điểm $M(1;2;3)$ và có vector pháp tuyến $\overrightarrow{n}(4;5;6)$ thì có phương trình là:
- A. $4(x-1)+5(y-2)+6(z-3)=0$
- B. $1(x-4)+2(y-5)+3(z-6)=0$
- C. $4x-4+5y-10+6z-18=0$
- D. $4x+5y+6z=32$
A, C, D
Mặt phẳng đi qua điểm $M(1;-2;3)$ và có vector pháp tuyến $\overrightarrow{n}(4;5;6)$ thì có phương trình là:
- A. $4(x-1)+5(y+2)+6(z-3)=0$
- B. $4(x-1)+5(y-2)+6(z-3)=0$
Mặt phẳng đi qua điểm $M(0;1;-1)$ và có vector pháp tuyến $\overrightarrow{n}(1;0;2)$ thì có phương trình là:
- A. $1(x-0)+0(y-1)+2(z+1)=0$
- B. $x+2z+1=0$
A, B
Mặt phẳng $x+2z+1=0$ có vector pháp tuyến là:
- A. $(1;2;1)$
- B. $(1;0;2)$
Mặt phẳng $2x-3y+4z=1$ chứa điểm:
- A. $M(0;0;1)$
- B. $N(2;1;0)$
Mặt phẳng $2x-3y+4z=1$ chứa điểm:
- A. $M(2;1;1)$
- B. $N(2;1;0)$
Xét các điểm $A(1;2;3), B(4;5;6)$. Mặt phẳng $(P)$ chứa $A$ và vuông góc với $AB$. Khi đó
- A. $\overrightarrow{AB}$ là vector pháp tuyến của $(P)$
- B. $\overrightarrow{BA}$ là vector pháp tuyến của $(P)$
- C. $\overrightarrow{AB}$ là vector chỉ phương của $(P)$
A, B
Xét các điểm $A(1;2;3), B(4;5;6)$. Mặt phẳng $(P)$ chứa $A$ và vuông góc với $AB$. Khi đó phương trình của $(P)$ là
- A. $-3(x-1)-3(y-2)-3(z-3)=0$
- B. $3(x-1)+3(y-1)+3(z-1)=0$
- C. $3(x-1)+3(y-2)+3(z-3)=0$
A, C
Nếu $\overrightarrow{a}=(4;5;6),\overrightarrow{b}=(7;8;9)$ thì $\left [\overrightarrow{a}, \overrightarrow{b} \right ]=$
- A. $4.7+5.8+6.9$
- B. $\left (5.9-6.8;6.7-4.9;4.8-5.7 \right )$
- C. 122
- D. $\left ( -3;6;-3 \right )$
B, D
Nếu mặt phẳng $(P)$ chứa $\overrightarrow{a}=(4;5;6),\overrightarrow{b}=(7;8;9)$ thì $\left [\overrightarrow{a}, \overrightarrow{b} \right ]$ là vector
- A. pháp tuyến của $(P)$
- B. chỉ phương của $(P)$
A
do $\overrightarrow{a}, \overrightarrow{b}$ ko cùng phương
Nếu mặt phẳng $(P)$ chứa $\overrightarrow{a}=(4;5;6),\overrightarrow{b}=(7;8;9)$ thì $\left [\overrightarrow{b}, \overrightarrow{a} \right ]$ là vector
- A. pháp tuyến của $(P)$
- B. chỉ phương của $(P)$
A
do $\overrightarrow{a}, \overrightarrow{b}$ ko cùng phương
Nếu mặt phẳng $(P)$ chứa $\overrightarrow{a}=(4;5;6),\overrightarrow{b}=(7;8;9)$ thì vector pháp tuyến của $(P)$ là:
- A. $\left ( -1;2;-1 \right )$
- B. $\left ( -3;6;-3 \right )$
- C. $\left ( 1;-2;1 \right )$
- D. $\left ( 3;-6;3 \right )$
A, B, C, D
Xét các điểm $A(1;2;3), B(4;5;6), C(7;8;9)$. Tọa độ $\overrightarrow{AB}=$
- A. $(3;3;3)$
- B. $(6;6;6)$
Xét các điểm $A(1;2;3), B(4;5;6), C(7;8;9)$. Tọa độ $\overrightarrow{AC}=$
- A. $(3;3;3)$
- B. $(6;6;6)$
Xét các điểm $A(1;2;3), B(4;5;6), C(7;8;9)$. Tọa độ $\left [\overrightarrow{AB}, \overrightarrow{AC} \right ]=$
- A. $(3;3;3)$
- B. $(6;6;6)$
- C. $(0;0;0)$
Xét các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Tọa độ $\overrightarrow{AB}=$
- A. $(3;3;3)$
- B. $(6;6;6)$
Xét các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Tọa độ $\overrightarrow{AC}=$
- A. $(3;3;3)$
- B. $(6;6;6)$
- C. $(7;6;5)$
Xét các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Tọa độ $\left [\overrightarrow{AB}, \overrightarrow{AC} \right ]=$
- A. $(3;3;3)$
- B. $(6;6;6)$
- C. $(0;0;0)$
- D. $(-3;6;-3)$
Mặt phẳng $(P)$ chứa các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Vector pháp tuyến của $(P)$ là
- A. $(3;3;3)$
- B. $(6;6;6)$
- C. $(0;0;0)$
- D. $(-3;6;-3)$
Mặt phẳng $(P)$ chứa các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Phương trình của $(P)$ là
- A. $-3(x-1)+6(y-2)-3(z-3)=0$
- B. $-3x+6y-3z+1=0$
A
do mặt phẳng đi qua điểm $A$ và có vector pháp tuyến là $(-3;6;-3)$
Mặt phẳng $(P)$ chứa các điểm $A(1;2;3), B(4;5;6), C(8;8;8)$. Phương trình của $(P)$ là
- A. $-3(x-1)+6(y-2)-3(z-3)=0$
- B. $-3x+6y-3z+2=0$
- C. $-3(x-4)+6(y-5)-3(z-6)=0$
- D. $-3(x-8)+6(y-8)-3(z-8)=0$
- E. $x-2y+z=0$
A, C, D, E
do mặt phẳng đi qua điểm $A,B,C$ và có vector pháp tuyến là $(-3;6;-3)$
Mặt phẳng đi qua gốc tọa độ có phương trình
- A. $x+y+z=0$
- B. $x+z=0$
- C. $x+y+z=1$
A, B
Mặt phẳng song song với 1 mặt phẳng tọa độ có phương trình
- A. $x+y+z=0$
- B. $x+z=0$
- C. $x+y+z=1$
- D. $x=1$
- E. $y=-2$
- F. $z=4$
D, E, F
Mặt phẳng nào có pháp tuyến vuông góc với $\overrightarrow{i}$?
- A. $x+y=0$
- B. $3x+z=0$
- C. $x+y+z=1$
- D. $y+2z=1$
Mặt phẳng nào có pháp tuyến vuông góc với $\overrightarrow{j}$?
- A. $x+y=0$
- B. $3x+z=0$
- C. $x+y+z=1$
- D. $y+2z=1$
Mặt phẳng nào có pháp tuyến vuông góc với $\overrightarrow{k}$?
- A. $x+y=0$
- B. $3x+z=0$
- C. $x+y+z=1$
- D. $y+2z=1$
Phương trình mặt phẳng theo đoạn chắn là:
- A. $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
- B. $a.x+b.y+c.z=1$
- C. $a.x+b.y+c.z=0$
- D. $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=0$
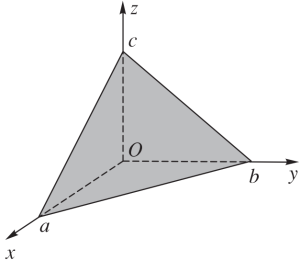
Mặt phẳng $(P)$ cắt các trục tọa độ tại các điểm có tọa độ $(2;0;0), (0;3;0), (0;0;4)$. Phương trình mặt phẳng $(P)$ là:
- A. $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$
- B. $2x+3y+4z=1$
- C. $2x+3y+4z=0$
- D. $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=0$

