Test5 | Hàm bậc 3
Đạo hàm của $x^3+3x^2-4$ là
- A. $2x^3+4x^2-5x+1$
- B. $3x^2+6x$
- C. $6x^2+8x-4$
$3x^2+6x=0$ khi $x=$
- A. -2
- B. 0
- C. 2
A, B
Trên khoảng $(-\infty ; -2)$ chọn $x=-3$. Nếu có $f'(x)=3x^2+6x$ thì $f'(-3)=$
- A. 9
- B. 8
- C. 0
Trên khoảng $(-\infty ; -2)$ chọn $x=-3$. Nếu có $f'(x)=3x^2+6x$ thì $f'(-3)$ là số
- A. âm
- B. dương
Trên khoảng $(-2 ; 0)$ chọn $x=-1$. Nếu có $f'(x)=3x^2+6x$ thì $f'(-1)=$
- A. -3
- B. -9
- C. 9
Trên khoảng $(-2 ; 0)$ chọn $x=-1$. Nếu có $f'(x)=3x^2+6x$ thì $f'(-1)$ là số
- A. âm
- B. dương
Trên khoảng $(0 ; +\infty)$ chọn $x=1$. Nếu có $f'(x)=3x^2+6x$ thì $f'(1)=$
- A. 3
- B. 6
- C. 9
Trên khoảng $(0 ; +\infty)$ chọn $x=1$. Nếu có $f'(x)=3x^2+6x$ thì $f'(1)$ là số
- A. dương
- B. âm
Trên khoảng $(-\infty ; -2)$, ta có $f'(x)>0$ nên $f(x)$
- A. đồng biến
- B. nghịch biến
Trên khoảng $( -2 ; 0)$, ta có $f'(x)<0$ nên $f(x)$
- A. đồng biến
- B. nghịch biến
Trên khoảng $(0 ; +\infty)$, ta có $f'(x)>0$ nên $f(x)$
- A. đồng biến
- B. nghịch biến
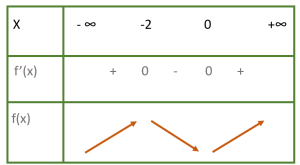
Theo bảng trên thì hàm số đạt cực đại khi $x=$
- A. -2
- B. 0

Theo bảng trên thì hàm số đạt cực tiểu khi $x=$
- A. -2
- B. 0

Hàm số $f(x)=x^3+3x^2-4$ có bảng biến thiên như trên sẽ có giá trị cực đại $f(-2)=$
- A. 0
- B. 1
- C. 2

Hàm số $f(x)=x^3+3x^2-4$ có bảng biến thiên như trên sẽ có giá trị cực tiểu $f(0)=$
- A. -4
- B. 0
- C. 2

Hàm số $f(x)=x^3+3x^2-4$ có bảng biến thiên như trên sẽ có giá trị cực đại là
- A. 0
- B. 1
- C. 2
- D. -2

Hàm số $f(x)=x^3+3x^2-4$ có bảng biến thiên như trên sẽ có giá trị cực tiểu là
- A. -3
- B. -4
- C. -2
- D. 0
Cho $f(x)=x^3+3x^2-4$ thì khi $x=1000$ thì $f(x)$
- A. rất lớn
- B. rất nhỏ
- C. bằng 0
Cho $f(x)=x^3+3x^2-4$. Khi $x=-1000$ thì $f(x)$
- A. rất lớn
- B. rất nhỏ
- C. bằng 0
Cho $f(x)=x^3+3x^2-4$ thì $\underset{x\rightarrow +\infty}{lim}f(x)=$
- A. $+\infty$
- B. $-\infty$
- C. 0
Cho $f(x)=x^3+3x^2-4$ thì $\underset{x\rightarrow -\infty}{lim}f(x)=$
- A. $+\infty$
- B. $-\infty$
- C. 0
Hàm $f(x)=x^3+3x^2-4$ có bảng biến thiên là
- A.
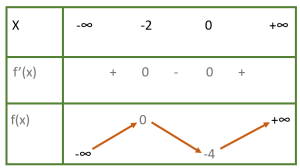
- B.
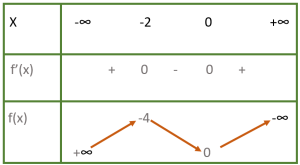
- C.
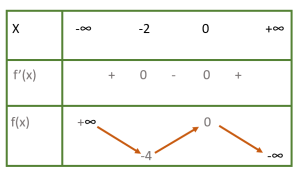
Hàm $f(x)$ với bảng biến thiên trên sẽ có đồ thị là
- A.
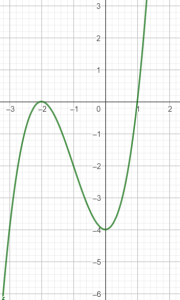
- B.
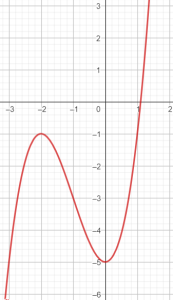
- C.
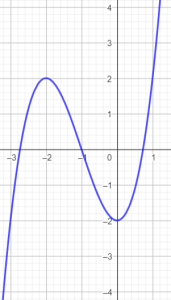
- D.
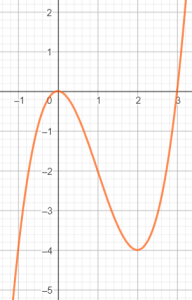
- E.
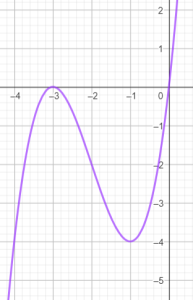

Giao điểm của đồ thị màu xanh với trục hoành là điểm có tọa độ $x=$
- A. -2
- B. 1
- C. 0
A, B

Giao điểm của đồ thị màu xanh với trục hoành là điểm có tọa độ $y=$
- A. -2
- B. 1
- C. 0

Giao điểm của đồ thị màu xanh với trục tung là điểm có tọa độ $x=$
- A. -4
- B. 0

Giao điểm của đồ thị màu xanh với trục tung là điểm có tọa độ $y=$
- A. -4
- B. 0
- C. -2
- D. 1

Giao điểm của đồ thị màu xanh với trục tung là điểm có tọa độ:
- A. $(0;-4)$
- B. $(-4;0)$

Giao điểm của đồ thị màu xanh với trục hoành là điểm có tọa độ:
- A. $(-2;0)$
- B. $(1;0)$
- C. $(-4;0)$
- D. $(0;-4)$
A, B

