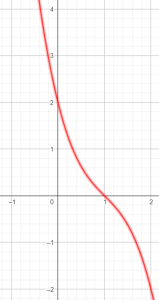
Test6 | Hàm bậc 3 ko cực trị mà f’=0
Cho $f(x)=-x^3+3x^2-4x+2$ thì $f'(x)=$
- A. $-3x^2+6x-4$
- B. $-3x^2+6x-2$
Nếu $f'(x)=-3x^2+6x-4$ thì $f'(x)=0$ khi $x=$
- A. 1
- B. 2
- C. ko có $x$ nào để $f'(x)=0$
Nếu $f'(x)=-3x^2+6x-4$ thì $f'(1)=$
- A. -1
- B. -2
Cho $f'(x)=-3x^2+6x-4$. Nếu biết $f'(x)$ luôn khác 0 và $f'(1)$ là số âm thì ta có thể nói $f'(x)$
- A. luôn âm
- B. luôn dương
Cho $f'(x)=-3x^2+6x-4$. Nếu biết $f'(x)$ luôn khác 0 thì có thể nói hàm $f(x)$
- A. có 1 cực đại
- B. ko có cực đại
- C. ko có cực tiểu
- D. luôn có cực tiểu
- E. có cực trị
- F. ko có cực trị
B, C, F
Nếu biết $f'(x)$ luôn âm thì ta có thể kết luận $f(x)$
- A. luôn nghịch biến
- B. luôn đồng biến
Cho $f(x)=-x^3+3x^2-4x+2$. Khi $x=1000$ thì $f(x)$
- A. rất nhỏ
- B. rất lớn
Nếu $f(x)=-x^3+3x^2-4x+2$ thì $\underset{x\rightarrow +\infty}{lim}f(x)=$
- A. $-\infty$
- B. $+\infty$
- C. 0
Cho $f(x)=-x^3+3x^2-4x+2$. Khi $x=-1000$ thì $f(x)$
- A. rất lớn
- B. rất nhỏ
- C. = 0
Nếu $f(x)=-x^3+3x^2-4x+2$ thì $\underset{x\rightarrow -\infty}{lim}f(x)=$
- A. $-\infty$
- B. $+\infty$
- C. 0
Hàm $f(x)=-x^3+3x^2-4x+2$ có bảng biến thiên là:
- A.
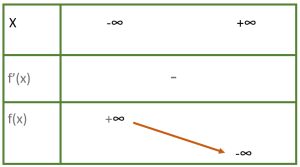
- B.
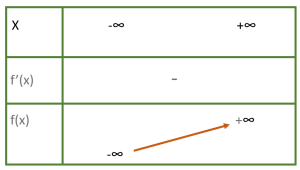
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục tung tại điểm có tọa độ $x=$
- A. 0
- B. 1
- C. $y$
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục hoành tại điểm có tọa độ $y=$
- A. 0
- B. 1
- C. $x$
Cho $f(x)=-x^3+3x^2-4x+2$ thì $f(0)=$
- A. 2
- B. 1
- C. 3
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục tung tại điểm có tọa độ $y=$
- A. 2
- B. 1
- C. 3
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục tung tại điểm có tọa độ
- A. $(0;2)$
- B. $(2;0)$
Cho $f(x)=-x^3+3x^2-4x+2$. Để có $f(x)=0$ thì $x=$
- A. 1
- B. -1
- C. 0
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục hoành tại điểm có tọa độ $x=$
- A. 1
- B. -1
- C. 0
- D. 2
Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ cắt trục hoành tại điểm có tọa độ
- A. $(1;0)$
- B. $(0;1)$

Đồ thị của hàm $f(x)=-x^3+3x^2-4x+2$ với bảng biến thiên trên là:
- A.
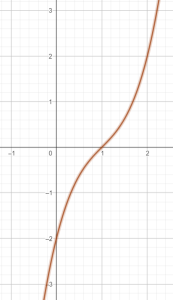
- B.