Toán 10 | Cơ bản
Chương 1.
Mệnh đề
Mệnh đề là 1 khẳng định đúng hoặc sai.
Mệnh đề đúng: là khẳng định đúng.
Mệnh đề sai: là khẳng định sai.
Mệnh đề ko thể vừa đúng vừa sai.
Ví dụ:
“4 chia hết cho 2” là mệnh đề đúng.
“5 chia hết cho 2” là mệnh đề sai.
“Trời nóng nực quá!” ko là mệnh đề vì chỉ là cảm giác, có thể đúng, cũng có thể sai.
Người ta thường dùng các chữ cái in hoa $P,Q,R,…$ để kí hiệu mệnh đề.
Mệnh đề chứa biến
“n chia hết cho 2” ko phải là mệnh đề, vì tính đúng sai tùy thuộc vào giá trị của $n$.
“n chia hết cho 2” được gọi là mệnh đề chứa biến.
Mệnh đề phủ định
Mệnh đề $P$: “4 chia hết cho 2”.
Mệnh đề phủ định của $P$ được kí hiệu là $\overline{P}$: “4 không chia hết cho 2”.
$P$ và $\overline{P}$ có tính đúng sai trái ngược nhau.
Mệnh đề $A$: “tam giác có 4 cạnh”.
Mệnh đề $\overline{A}$: “tam giác có số cạnh khác 4”.
Thường ta sẽ dùng từ “không” hoặc từ “khác” với mệnh đề phủ định.
Mệnh đề $B$: $2^5>3^4$.
Mệnh đề $\overline{B}$: $2^5 \leq 3^4$.
Mệnh đề kéo theo
Cho 2 mệnh đề $P,Q$. Mệnh đề kéo theo là:
- “Nếu $P$ thì $Q$”, kí hiệu là $P\Rightarrow Q$
- “Nếu $Q$ thì $P$”, kí hiệu là $Q\Rightarrow P$
Mệnh đề $P\Rightarrow Q$ chỉ sai khi $P$ đúng và $Q$ sai.
Mệnh đề $Q\Rightarrow P$ chỉ sai khi $Q$ đúng và $P$ sai.
Khi mệnh đề $P\Rightarrow Q$, ta nói:
- $P$ là giả thiết, $Q$ là kết luận
- $P$ là điều kiện đủ để có $Q$
- $Q$ là điều kiện cần để có $P$
Mệnh đề đảo
$Q\Rightarrow P$ là mệnh đề đảo của $P\Rightarrow Q$.
Hai mệnh đề tương đương
Khi ta nói “$P$ tương đương $Q$”, hoặc nói “$P$ khi và chỉ khi $Q$”, kí hiệu $P\Leftrightarrow Q$, có nghĩa là:
- $P\Rightarrow Q$ đúng, và
- $Q\Rightarrow P$ đúng
Khi đó, ta cũng nói $P$ là điều kiện cần và đủ để có $Q$, hoặc $Q$ là điều kiện cần và đủ để có $P$.
$P,Q$ tương đương nhau khi $P,Q$ cùng đúng, hoặc cùng sai.
Mệnh đề chứa kí hiệu $\exists ,\forall $
$\exists$: đọc là tồn tại, ý nghĩa là “có một cái nào đó”.
$\forall $: đọc là với mọi, ý nghĩa là “với tất cả mọi cái”.
Mệnh đề chứa biến: chưa biết tính đúng sai.
Kết hợp các kí hiệu $\exists ,\forall $ với mệnh đề chứa biến để tạo ra mệnh đề $\rightarrow $ biết được tính đúng sai.
Ví dụ:
Mệnh đề chứa biến: “$x>5$ $”\rightarrow $ chưa biết đúng hay sai.
- Thêm kí hiệu $\exists$ vào: “$\exists x\in \mathbb{N}, x>5$” $\rightarrow $ đúng vì có $x=6\in \mathbb{N}, x>5$.
- Thêm kí hiệu $\forall $ vào: ” $\forall x\in \mathbb{N}, x>5$” $\rightarrow $ sai vì không phải bất cứ $x$ nào trong $\mathbb{N}$ đều có $x>5$.
Test1 | Mệnh đề
Tập hợp
Tập hợp: gồm 1 nhóm đối tượng. Mỗi đối tượng được gọi là 1 phần tử.
Các tập hợp thường được kí hiệu bằng các chữ cái in hoa: $A,B,C,…$
Các phần tử của tập hợp thường được kí hiệu bằng các chữ cái in thường: $a,b,c,…$
Các phần tử của tập hợp được viết trong 2 dấu ngoặc nhọn “{}”, cách nhau bởi dấu “;”.
Để chỉ $a$ là 1 phần tử của tập hợp A, ta viết $a\in A$, đọc là $a$ thuộc $A$.
Ngược lại, $a$ không phải là 1 phần tử của $A$, ta viết $a\notin A$, đọc là $a$ không thuộc $A$.
Tập hợp rỗng: là tập hợp không chứa phần tử nào, kí hiệu là $\emptyset$.
Cách xác định tập hợp
Cách liệt kê các phần tử:
$A=\{0;2;4;6;8;10\}$.
Cách chỉ ra tính chất đặc trưng:
$A=\{ x|x\in\mathbb{N}, x \text{ chẵn và } x<12 \}$.
Các phần tử có thể viết theo thứ tự tùy ý:
$A=\{0;2;4;6;8;10\}=\{8;10;4;6;2;0\}$.
Các phần tử chỉ liệt kê 1 lần:
Tập hợp các chữ cái trong từ “beginning” là $B=\{b;e;g;i;n\}$.
Nếu quy tắc xác định các phần tử đủ rõ thì người ta dùng dấu “…” mà không cần phải viết tất cả các phần tử của tập hợp.
Tập hợp các số tự nhiên nhỏ hơn 100 là: $\{0;1;2;3;4;5;…;99\}$.
Tập hợp hữu hạn: có thể đếm hết số lượng phần tử.
Số phần tử của tập hợp $A$ được kí hiệu là $n(A)$.
Nếu $A=\{0;2;4;6;8;10\}$ thì $n(A)=6$.
Tập hợp vô hạn: không thể đếm hết số lượng phần tử.
$B=\{1;2;3;4;5;…\}$ là tập hợp vô hạn.
Số phần tử của tập hợp rỗng: $n(\emptyset)=0$.
Tập hợp con
Nếu mọi phần tử của $A$ đều là phần tử của $B$ thì ta nói $A$ là tập hợp con của $B$, kí hiệu $A\subset B$, đọc là $A$ chứa trong $B$, hoặc $B\supset A$, đọc là $B$ chứa $A$.
Nếu $A$ không phải là tập hợp con của $B$, ta viết $A\not\subset B$, đọc là $A$ không chứa trong $B$, hoặc $B$ không chứa $A$.
Nhận xét: $A\subset A$ và $\emptyset\subset A$ với $A$ là bất kì tập hợp nào.
Biểu đồ Ven:
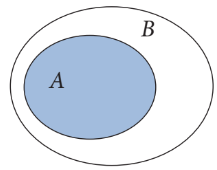
$A\subset B$.
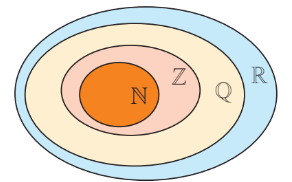
$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}$.
Hai tập hợp bằng nhau
$A=B$ nếu có $A\subset B$ và $B\subset A$.
Một số tập hợp con của tập hợp số thực

Chú ý các dấu:
- “[,]”: 2 bên có thể bằng
- “(,)”: 2 bên không bằng
- “[,)”: bên trái bằng, bên phải không bằng
- “(,]”: bên trái không bằng, bên phải bằng
- “$+\infty $”: đọc là dương vô cùng
- “$-\infty $”: đọc là âm vô cùng
- kề bên $\infty$ luôn dùng các dấu “),(“
Test2 | Tập hợp
Test3 | Tập hợp con
Test4 | Tập hợp con của R
Hợp và giao của các tập hợp
Hợp của $A,B$ kí hiệu là: $A\cup B$.
$A\cup B=\{x|x\in A\text{ hoặc } x\in B\}$.
Hợp: gom lại.
Giao của $A,B$ kí hiệu là: $A\cap B$.
$A\cap B=\{x|x\in A\text{ và } x\in B\}$.
Giao: chỉ lấy phần giống nhau.
Hiệu của 2 tập hợp
Các phần tử thuộc $A$ mà không thuộc $B$, kí hiệu là $A\setminus B$, gọi là hiệu của $A$ và $B$.
$A\setminus B=\{x|x\in A\text{ và }x\notin B\}$.
Nếu $A$ là tập hợp con của $E$ thì hiệu $E\setminus A$ được gọi là phần bù của $A$ trong $E$, kí hiệu là $C_E A$.
Test5 | Các phép toán trên tập hợp
Chương 2.
Bất phương trình bậc nhất 2 ẩn có 1 trong các dạng sau:
- $ax+by+c>0$
- $ax+by+c<0$
- $ax+by+c\geq 0$
- $ax+by+c\leq 0$
trong đó, $a,b,c$ là các số cho trước; $a,b$ không đồng thời bằng 0; $x,y$ là các ẩn.
Nghiệm của bất phương trình bậc nhất 2 ẩn
Mỗi cặp số $(x_0;y_0)$ thỏa mãn $ax_0+by_0+c>0$ được gọi là 1 nghiệm của bất phương trình $ax+by+c>0$.
Biểu diễn miền nghiệm của bất phương trình bậc nhất 2 ẩn
Trong mặt phẳng tọa độ $Oxy$, tập hợp các điểm $(x_0;y_0)$ thỏa mãn $ax_0+by_0+c>0$ được gọi là miền nghiệm của bất phương trình $ax+by+c>0$.
3 bước để Biểu diễn miền nghiệm của bất phương trình $ax+by+c>0$:
- Trên mặt phẳng $Oxy$, vẽ đường thẳng $d: ax+by+c=0$.
- Lấy một điểm $(x_0;y_0)$ tùy ý sao cho không thuộc $d$. Tính $ax_0+by_0+c$.
- Kết luận
- Nếu $ax_0+by_0+c>0$ thì miền nghiệm của bất đẳng thức đã cho là nửa mặt phẳng chứa điểm $(x_0;y_0)$.
- Nếu $ax_0+by_0+c<0$ thì miền nghiệm của bất đẳng thức đã cho là nửa mặt phẳng không chứa điểm $(x_0;y_0)$.
Chú ý:
- Nếu bất phương trình chứa dấu “$>,<$” thì miền nghiệm là nửa mặt phẳng không chứa đường thẳng $d$.
- Nếu bất phương trình chứa dấu “$\leq,\geq$” thì miền nghiệm là nửa mặt phẳng chứa đường thẳng $d$.
Hệ bất phương trình bậc nhất 2 ẩn là hệ gồm 2 hay nhiều bất phương trình bậc nhất 2 ẩn.
Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là nghiệm của hệ bất phương trình đã cho.
Tập hợp các điểm $(x_0;y_0)$ có tọa độ là nghiệm của hệ bất phương trình được gọi là miền nghiệm của nó.
Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn:
- Biểu diễn miền nghiệm của mỗi bất phương trình của hệ trong cùng 1 mặt phẳng tọa độ.
- Phần giao của các miền nghiệm chính là miền nghiệm của hệ.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức $F=ax+by$ trên 1 miền đa giác
$F$ đạt giá trị lớn nhất hoặc nhỏ nhất tại 1 trong các đỉnh của đa giác.
Chương 3.
Hàm số
Với mỗi giá trị $x$ thuộc tập hợp số $D$, ta xác định được 1 giá trị duy nhất là $y$ trong $\mathbb{R}$ thì ta có 1 hàm số.
Ta gọi:
- $x$ là biến số
- $y$ là hàm số của $x$
- $D$ là tập xác định của hàm số
- Tập hợp $T$ gồm tất cả các giá trị $y$ gọi là tập giá trị của hàm số
Ta thường dùng kí hiệu $f(x)$ để chỉ giá trị $y$ tương ứng với $x$, nên hàm số còn được viết là $y=f(x)$.
Đồ thị của hàm số
Cho hàm số $y=f(x)$ có tập xác định $D$.
Trên mặt phẳng tọa độ $Oxy$, đồ thị $(C)$ của hàm số là tập hợp tất cả các điểm $M(x;y)$ với $x\in D$ và $y=f(x)$.
Hàm số đồng biến, nghịch biến
Hàm số $f(x)$ đồng biến trên khoảng $(a;b)$ nếu: $\forall x_1,x_2\in(a;b),x_1<x_2\Rightarrow f(x_1)<f(x_2)$.
Hàm số $f(x)$ nghịch biến trên khoảng $(a;b)$ nếu: $\forall x_1,x_2\in(a;b),x_1<x_2\Rightarrow f(x_1)>f(x_2)$.
Hàm số bậc 2
Hàm số bậc 2 theo biến $x$ là hàm số có dạng: $y=f(x)=ax^2+bx+c$ với $a,b,c$ là các số thực và $a$ khác 0.
Tập xác định của hàm số bậc 2 là $\mathbb{R}$.
Đồ thị của hàm số bậc 2
Đồ thị của hàm bậc 2: $y=ax^2+bx+c$ là một parabol $(P)$:
- có đỉnh $S$ có hoành độ $x_S=-\frac{b}{2a}$, tung độ $y_S=-\frac{b^2-4ac}{4a}$
- có trục đối xứng là đường thẳng $d: x=-\frac{b}{2a}$
- có bề lõm quay lên trên nếu $a>0$, hoặc quay xuống nếu $a<0$
- cắt trục tung tại điểm có tung độ bằng $c$, tức là đồ thị đi qua điểm $(0;c)$.
5 bước để vẽ đồ thị của hàm bậc 2: $y=ax^2+bx+c$:
- Xác định tọa độ đỉnh $S(-\frac{b}{2a};-\frac{b^2-4ac}{4a})$
- Vẽ trục đối xứng $d: x=-\frac{b}{2a}$
- Tìm tọa độ giao điểm của đồ thị với trục tung $A(0;c)$ và với trục hoành (khi $y=0$).
- Xác định điểm đối xứng với $A$ qua $d$, là điểm $B(\frac{-b}{a};c)$
- Vẽ parabol có đỉnh $S$, trục đối xứng $d$, đi qua các điểm tìm được.
Để cho ngắn gọn, ta đặt: $\Delta =b^2-4ac$.
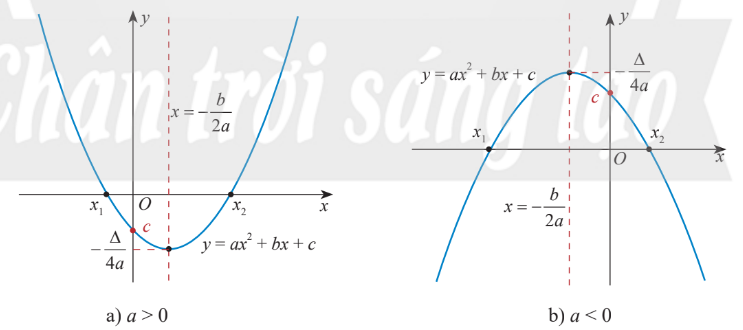
Sự biến thiên của hàm số bậc 2
Dựa vào đồ thị, ta có thể tóm tắt sự biến thiên của hàm bậc 2 như sau:

Từ bảng trên, ta thấy:
- Khi $a>0$, $f(x)$ nhỏ nhất và bằng $-\frac{\Delta }{4a}$ tại $x=-\frac{b}{2a}$ và có tập giá trị là $T=[-\frac{\Delta }{4a};+\infty )$
- Khi $a<0$, $f(x)$ lớn nhất và bằng $-\frac{\Delta }{4a}$ tại $x=-\frac{b}{2a}$ và có tập giá trị là $T=(-\infty;-\frac{\Delta }{4a} ]$
Chương 4.
Giá trị lượng giác
Nửa đường tròn đơn vị: là nửa đường tròn có bán kính bằng 1.
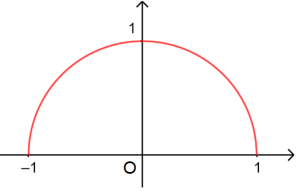
Với mỗi góc $a$ (từ $0^o$ đến $180^o$), ta xác định 1 điểm $M$ duy nhất trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=a$.
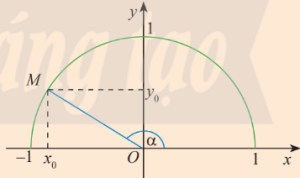
Giả sử tọa độ của $M$ là $x_0;y_0$. Khi đó, ta có các giá trị lượng giác của $a$:
- $\sin a=y_0$
- $\cos a=x_0$
- Nếu $x_0\neq 0$ thì $\tan a=\frac{y_o}{x_0}$
- Nếu $y_0\neq 0$ thì $\cot a=\frac{x_o}{y_0}$
Quan hệ giữa các giá trị lượng giác
$\cos a=\sin(90^o-a)$
$\sin a=\cos(90^o-a)$
$\tan a=\cot(90^o-a)$
$\cot a=\tan(90^o-a)$
$\sin a=\sin(180^o-a)$
$\cos a=-\cos(180^o-a)$
$\tan a=-\tan(180^o-a)$
$\cot a=-\cot(180^o-a)$
Cách xác định góc khi biết giá trị lượng giác
Với góc $a$ từ $0^o$ đến $180^o$:
- Nếu $\sin a=b$ thì $a=\sin^{-1}b$
- Nếu $\cos a=b$ thì $a=\cos^{-1}b$
- Nếu $\tan a=b$ thì $a=\tan^{-1}b$
- Nếu $\cot a=b$ thì $a=\cot^{-1}b$
Chú ý trên máy tính thường sẽ không có nút “$\cot^{-1}$”.
Cho nên, nếu có $\cot a=b$ thì ta tính $\tan a=\frac{1}{\cot a}=\frac{1}{b}$. Suy ra $a=\tan^{-1}\frac{1}{b}$.
Định lí $\cos$ trong tam giác
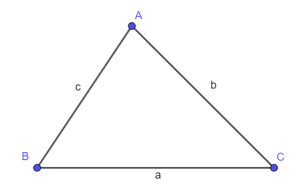
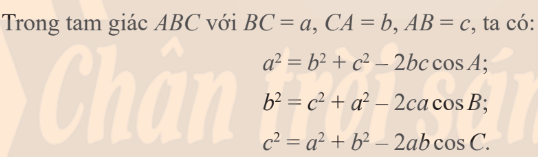
Để dễ nhớ, để ý $a$ là cạnh đối diện góc $A$, còn $b,c$ là các cạnh 2 bên góc $A$.
Từ các tính chất trên, ta suy ra:
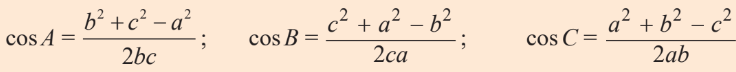
Định lí $\sin$ trong tam giác
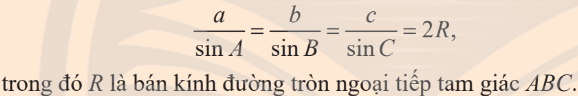
Từ tính chất trên, ta suy ra:
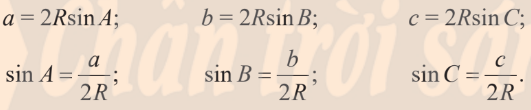
Các công thức tính diện tích tam giác
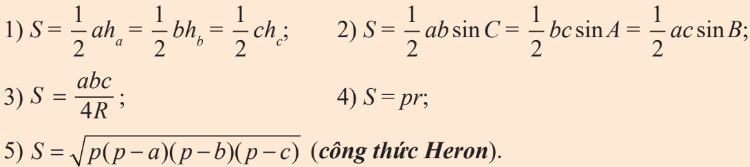
Giải tam giác
Là tìm số đo các cạnh và các góc của tam giác.
Chương 5.
Vector
Là đoạn thẳng có hướng, có điểm đầu và điểm cuối.
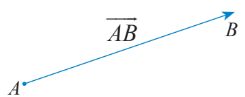
Vector có điểm đầu là $A$, điểm cuối là $B$ được kí hiệu là $\overrightarrow{AB}$, đọc là vectơ $AB$.
Giá của $\overrightarrow{AB}$: là đường thẳng đi qua 2 điểm $A,B$.
Độ dài $\overrightarrow{AB}$: là độ dài đoạn thẳng $AB$, kí hiệu là $|\overrightarrow{AB}|$. Khi đó, ta có $|\overrightarrow{AB}|=AB$.
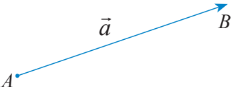
Khi không cần quan tâm điểm đầu và điểm cuối của vector, dùng kí hiệu: $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},…$
2 vector cùng phương, cùng hướng
2 vector cùng phương: giá của chúng song song hoặc trùng nhau.
Khi cùng phương, thì có thể: cùng hướng hoặc ngược hướng.
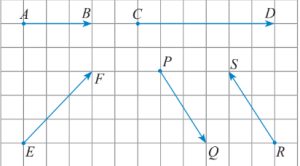
Trong hình trên, $\overrightarrow{AB},\overrightarrow{CD}$ cùng phương và cùng hướng.
Còn $\overrightarrow{PQ},\overrightarrow{RS}$ cùng phương và ngược hướng.
$\overrightarrow{EF},\overrightarrow{PQ}$ thì không cùng phương.
Vector bằng nhau, đối nhau
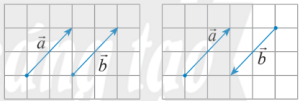
$\overrightarrow{a},\overrightarrow{b}$ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu $\overrightarrow{a}=\overrightarrow{b}$.
$\overrightarrow{a},\overrightarrow{b}$ được gọi là đối nhau nếu chúng ngược hướng và cùng độ dài, kí hiệu $\overrightarrow{a}=-\overrightarrow{b}$.
$\overrightarrow{AB}=-\overrightarrow{BA}$
$-\overrightarrow{CD}=\overrightarrow{DC}$
Vector không
là vector có điểm đầu và điểm cuối trùng nhau, kí hiệu là $\overrightarrow{0}$.
Các vector không: $\overrightarrow{0}=\overrightarrow{AA}=\overrightarrow{BB}=…$
- đều bằng nhau
- có độ dài bằng 0
- cùng phương, cùng hướng, ngược hướng với mọi vector
Tổng 2 vector
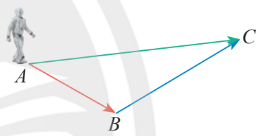
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
Để ý 2 chữ $B$ ở giữa phải giống nhau, và kết quả nhận được thì bỏ 2 chữ $B$ đó đi, giữ 2 chữ còn lại là $A,C$.
Với 3 điểm $M,N,P$ tùy ý, ta cũng có $\overrightarrow{MN}+\overrightarrow{NP}=\overrightarrow{MP}$.
Quy tắc hình bình hành
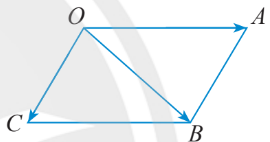
Nếu $OABC$ là hình bình hành thì $\overrightarrow{OA}+\overrightarrow{OC}=OB$.
Tổng 2 vector chung điểm đầu $O$ là vector đường chéo có điểm đầu cũng là $O$.
Tính chất của phép cộng vector
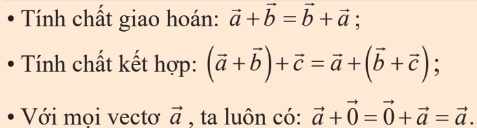
Hiệu của 2 vector
$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$
Tính chất vector của trung điểm đoạn thẳng
![]()
Khi $M$ là trung điểm của đoạn $AB$ thì ta có $\overrightarrow{MB}=\overrightarrow{AM}$ nên
$\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AM}=\overrightarrow{MM}=\overrightarrow{0}$
Tính chất vector của trọng tâm tam giác
Nhắc lại kiến thức cũ: trọng tâm tam giác là giao điểm của 3 đường trung tuyến.
Khi $G$ là trọng tâm tam giác $ABC$ thì $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
Cho số $k\in\mathbb{R}$, vector $k\overrightarrow{a}$ là vector có độ dài gấp $k$ lần vector $\overrightarrow{a}$ và
- nếu $k>0$ thì $k\overrightarrow{a}$ cùng chiều với $\overrightarrow{a}$
- nếu $k<0$ thì $k\overrightarrow{a}$ ngược chiều với $\overrightarrow{a}$
Để ý: $0\overrightarrow{a}=k\overrightarrow{0}=\overrightarrow{0}$
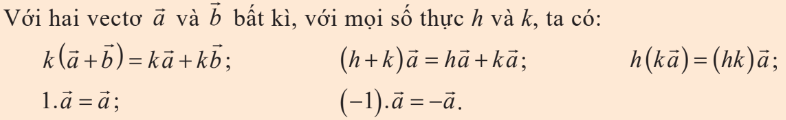
Điều kiện để 2 vector cùng phương
$\overrightarrow{a},\overrightarrow{b}$ (khác $\overrightarrow{0}$) cùng phương khi và chỉ khi có số $k$ sao cho: $\overrightarrow{a}=k\overrightarrow{b}$
Góc giữa 2 vector
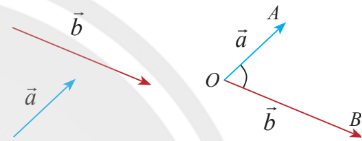

Để ý:
- $(\overrightarrow{a},\overrightarrow{b})=(\overrightarrow{b},\overrightarrow{a})$
- góc giữa 2 vector cùng hướng thì bằng $0^o$
- góc giữa 2 vector ngược hướng thì bằng $180^o$
Quy ước: nếu $\overrightarrow{a}$ hoặc $\overrightarrow{b}$ bằng $\overrightarrow{0}$ thì $(\overrightarrow{a},\overrightarrow{b})$ bằng số tùy ý giữa $0^o$ và $180^o$.
Tích vô hướng của 2 vector
$\overrightarrow{a}.\overrightarrow{b}=|\overrightarrow{a}|.|\overrightarrow{b}|.\cos(\overrightarrow{a},\overrightarrow{b})$.
Để ý:
- nếu $\overrightarrow{a}$ hoặc $\overrightarrow{b}$ bằng $\overrightarrow{0}$ thì $\overrightarrow{a}.\overrightarrow{b}=0$
- $\overrightarrow{a}\perp \overrightarrow{b}$ khi và chỉ khi $\overrightarrow{a}.\overrightarrow{b}=0$
Bình phương vô hướng của $\overrightarrow{a}$: khi $\overrightarrow{a}=\overrightarrow{b}$ thì $\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{a}^2$.
Ta có $\overrightarrow{a}^2=|\overrightarrow{a}|.|\overrightarrow{a}
|.\cos 0^o=|\overrightarrow{a}|^2$
Tính chất của tích vô hướng
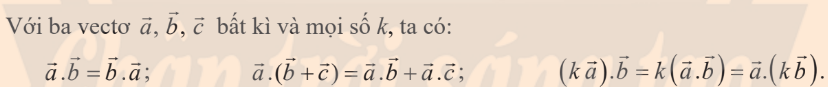
Chương 6.
Số gần đúng
Do cách đo và dụng cụ đo khác nhau dẫn đến các kết quả đo khác nhau.
Sai số tuyệt đối
Giả sử số đúng là $\overline{a}$, số gần đúng là $a$.
Sai số tuyệt đối của $a$ là: $\Delta_a= |\overline{a}-a|$.
Sai số tương đối
Sai số tương đối của $a$ là: $\delta_a=\frac{\Delta_a }{|a|} $
Quy tắc làm tròn số
Từ 5 trở lên thì tăng số bên trái lên 1 đơn vị:
$1,37\approx 1,4$ (số 7 lớn hơn 5)
$2,5\approx 3,0$ (số 5)
Nhỏ hơn 5 thì giữ nguyên số bên trái:
$3,41\approx 3,4$ (số 1 nhỏ hơn 5)
$5,392\approx 5,39$ (số 2 nhỏ hơn 5)
Xác định số quy tròn của số gần đúng
Cách xác định số quy tròn của số gần đúng $a$ với độ chính xác $d$:
- Tìm hàng của chữ số khác 0 đầu tiên bên trái $d$.
- Quy tròn số $a$ ở hàng gấp 10 lần số tìm được ở bước 1.
Cho $a=1903,d=50$.
Số khác 0 bên trái của $d$ là số 5 và ở hàng chục.
Gấp 10 lần hàng chục là hàng trăm. Nên ta sẽ quy tròn $a$ đến hàng trăm.
Vậy số quy tròn của $a$ là 1900.
Cho $\overline{b}=0,1891\pm 0,004$.
Với cách viết trên, số gần đúng là $b=0,1891$, độ chính xác $d=0,0047$.
Số khác 0 bên trái của $d$ là số 4 và ở hàng phần nghìn.
Gấp 10 lần hàng phần nghìn là hàng phần trăm. Nên ta sẽ quy tròn $b$ đến hàng phần trăm.
Vậy số quy tròn của $b$ là 0,19.
Xác định số gần đúng của một số
Cách xác định số gần đúng $a$ của số đúng $\overline{a}$ với độ chính xác $d$:
- Tìm hàng của chữ số khác 0 đầu tiên bên trái $d$.
- Quy tròn số $\overline{a}$ ở hàng vừa tìm được ở bước 1.
Cho $\overline{a}=\frac{12}{7}=1,714285…, d=0,00231$.
Số khác 0 bên trái của $d$ là số 2 và ở hàng phần nghìn.
Quy tròn $\overline{a}$ đến hàng phần nghìn ta được số gần đúng $a=1,714$.
Cho $\overline{b}=\frac{1-\sqrt{5}}{2}=-0,61803398…,d=0,00089$.
Số khác 0 bên trái của $d$ là số 8 và ở hàng phần chục nghìn.
Quy tròn $\overline{b}$ đến hàng phần chục nghìn ta được số gần đúng $b=-0,6180$.
Bảng số liệu



Biểu đồ
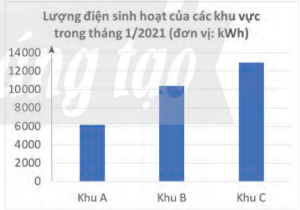
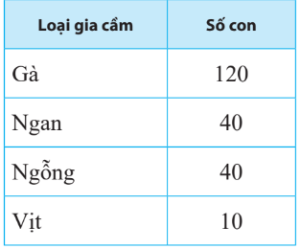
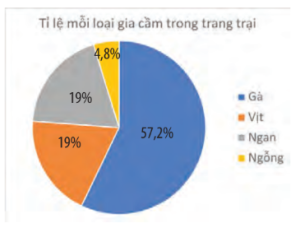
Số trung bình
Giả sử có mẫu số liệu: $x_1,x_2,x_3,…,x_n$.
Số trung bình (hay còn gọi là số trung bình cộng) kí hiệu là $\overline{x}$, được tính bởi công thức: $\overline{x}=\frac{x_1+x_2+…+x_n}{n}$.
Nếu mẫu số liệu được cho dạng bảng tần số:
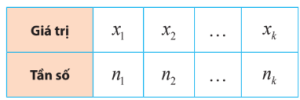
thì công thức tính số trung bình trở thành:
$\overline{x}=\frac{n_1.x_1+n_2.x_2+…+n_k.x_k}{n}$ với $n=n_1+n_2+…+n_k$.
Ta gọi $n$ là cỡ mẫu.
Tần số tương đối của $x_k$ là: $f_k=\frac{n_k}{n}$.
Ý nghĩa của số trung bình: đại diện cho các số liệu của mẫu, đo xu thế trung tâm của mẫu
Trung vị
Khi các số liệu của mẫu có độ chênh lệch lớn, số trung bình không còn phản ánh đúng đặc trưng của mẫu. Khi đó, ta dùng số trung vị.
Số trung vị được tính như sau:

Ý nghĩa của số trung vị: là giá trị nằm chính giữa mẫu số liệu đã sắp xếp. Khi mẫu có số liệu rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì không.
Tứ phân vị
Trung vị chia mẫu thành 2 phần.
Tứ phân vị chia mẫu thành 4 phần.
Tứ phân vị gồm 3 số, được xác định như sau:

Ý nghĩa của tứ phân vị: chia mẫu số liệu đã sắp xếp thành 4 phần, mỗi phần gồm 25% số liệu.
$Q_1$: là tứ phân vị dưới.
$Q_3$: là tứ phân vị trên.
Mốt (Mode)
Là giá trị có tần số lớn nhất, kí hiệu là $M_0$.
Ý nghĩa của Mốt: đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.
Một mẫu số liệu có thể có nhiều mốt.
Quy ước: khi tất cả các số liệu của mẫu đều bằng nhau thì mẫu đó không có mốt.
Mẫu số liệu được gọi là:
- đối xứng: khi trung bình bằng trung vị
- lệch trái nếu trung bình nhỏ hơn trung vị
- lệch phải nếu trung bình lớn hơn trung vị
Khoảng biến thiến và khoảng tứ phân vị

Ý nghĩa của khoảng biến thiên: đặc trung cho độ phân tán của mẫu.
Ý nghĩa của khoảng tứ phân vị: đặc trung cho độ phân tán của một nửa số liệu từ $Q_1$ đến $Q_3$.
Khoảng tứ phân vị không bị ảnh hưởng bởi giá trị rất lớn hoặc rất bé trong mẫu.
Giá trị ngoại lệ
Là giá trị quá nhỏ hoặc quá lớn so với đa số giá trị của mẫu.
$x$ là giá trị ngoại lệ nếu: $x>Q_3+1,5\Delta_Q$ hoặc $x<Q_1-1,5\Delta_Q$.
Giá trị ngoại lệ làm cho số trung bình thay đổi lớn, và không phản ánh tốt đặc trưng của mẫu. Khi có giá trị ngoại lệ trong mẫu, ta thường dùng trung vị hơn là số trung bình để biết đặc trưng mẫu.
Phương sai và độ lệch chuẩn
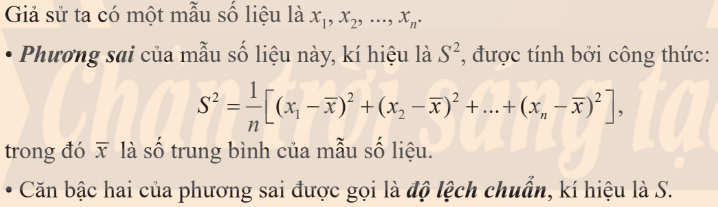
Có thể biến đổi công thức phương sai thành: $S^2=\frac{1}{n}(x_1^2+x_2^2+…+x_n^2)-\overline{x}^2$.
Phương sai mẫu hiệu chỉnh: $\widehat{s}^2=\frac{nS^2}{n-1}$.
Ý nghĩa của phương sai và độ lệch chuẩn: dùng để đo mức độ phân tán của mẫu quanh số trung bình.

Chương 7.
Tam thức bậc 2
Là đa thức bậc hai: $f(x)=ax^2+bx+c$ với $a,b,c$ là các hệ số, và $a$ khác 0.
Giá trị của tam thức bậc 2 tại $x_0$ là: $f(x_0)=ax_0^2+bx_0+c$
Nghiệm của tam thức bậc hai $f(x)$: là nghiệm của phương trình $ax^2+bx+c=0$.
Biệt thức của $f(x)$: $\Delta =b^2-4ac$.
Biệt thức thu gọn: $\Delta’ =\left ( \frac{b}{2}\right )^2-ac$.
Dấu của tam thức bậc 2


Giải bất phương trình bậc 2 là tìm tập hợp nghiệm của nó.
Phương trình dạng $\sqrt{ax^2+bx+c}=\sqrt{dx^2+ex+f}$

Phương trình dạng $\sqrt{ax^2+bx+c}=dx+e$

Chương 8.
Quy tắc cộng
Giả sử 1 công việc được thực hiện theo phương án $A$ hoặc phương án $B$. Phương án $A$ có $m$ cách thực hiện. Phương án $B$ có $n$ cách thực hiện và không trùng với phương án $A$. Khi đó, công việc này có thể thực hiện theo $m+n$ cách.
Quy tắc nhân
Giả sử 1 công việc được chia làm 2 công đoạn. Công đoạn 1 có $n$ cách thực hiện. Ứng với mỗi cách đó có $n$ cách thực hiện công đoạn 2. Khi đó, công việc có thể được thực hiện theo $m.n$ cách.
Hoán vị
Cho tập hợp $A$ có $n$ phần tử ($n\geq 1$).
Mỗi cách sắp xếp $n$ phần tử của tập hợp $A$ theo 1 thứ tự gọi là 1 hoán vị của các phần tử đó, còn gọi là hoán vị của $A$, hay hoán vị của $n$ phần tử.
Kí hiệu $P_n$ là số hoán vị của $n$ phần tử.
$P_n=n(n-1)(n-2)…2.1.$
Kí hiệu: $n!=n(n-1)(n-2)…2.1.$
Khi đó $P_n=n!$
Quy ước: $0!=1.$
Chỉnh hợp
Cho tập hợp $A$ có $n$ phần tử ($n\geq 1$) và số nguyên $k$ với $1\leq k\leq n$.
Mỗi cách lấy $k$ phần tử của $A$ và sắp xếp chúng theo 1 thứ tự gọi là 1 chỉnh hợp chập $k$ của $n$ phần tử đó.
Kí hiệu $A^k_n$ là số chỉnh hợp chập $k$ của $n$ phần tử.
$A^k_n=n(n-1)(n-2)…(n-k+1)=\frac{n!}{(n-k)!}$.
Tổ hợp
Cho tập hợp $A$ có $n$ phần tử ($n\geq 1$) và số nguyên $k$ với $1\leq k\leq n$.
Mỗi tập hợp con gồm $k$ phần tử của $A$ được gọi là 1 tổ hợp chập $k$ của $n$ phần tử.
Kí hiệu $C^k_n$ là số tổ hợp chập $k$ của $n$ phần tử.
$C^k_n=\frac{n!}{k!(n-k)!}$.
Quy ước: $C^0_n=1$.
Nhận xét: $C^k_n=C^{n-k}_n$,
$A^k_n=k!.C^k_n$.
Chương 9.
Trục tọa độ


Hệ trục tọa độ

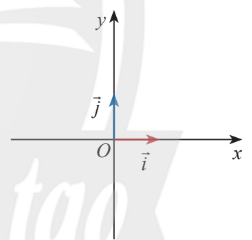
Mặt phẳng mà trên đó đã cho 1 hệ trục tọa độ $Oxy$ được gọi là mặt phẳng tọa độ $Oxy$, gọi tắt là mặt phẳng $Oxy$.
Tọa độ của 1 vector
Nếu $\overrightarrow{a}=x.\overrightarrow{i}+y.\overrightarrow{j}$ thì $(x;y)$ được gọi là tọa độ của $\overrightarrow{a}=(x;y)$, $x$ được gọi là hoành độ, $y$ được gọi là tung độ của $\overrightarrow{a}$.
Tọa độ của 1 điểm
Tọa độ của điểm $M$: chính là tọa độ của $\overrightarrow{OM}$.
M(x;y)\Leftrightarrow \overrightarrow{OM}=(x;y)\Leftrightarrow \overrightarrow{OM}=x.\overrightarrow{i}+y.\overrightarrow{j}.
Ta cũng có thể kí hiệu tọa độ điểm $M$ theo cách là: $M(x_M;y_M)$.
Biểu thức tọa độ của các phép toán vector
Cho $\overrightarrow{a}=(x_a;y_a),\overrightarrow{b}=(x_b;y_b)$ và số thực.
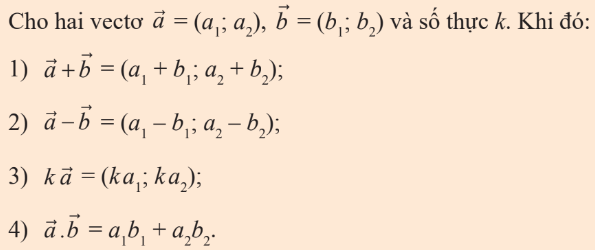
Tọa độ điểm và vector
$\overrightarrow{AB}=(x_B-x_A;y_B-y_A)$.
Tọa độ trung điểm và trọng tâm
Tọa độ trung điểm $M$ của đoạn thẳng $AB$ là: $M\left ( \frac{x_A+x_B}{2};\frac{y_A+y_B}{2} \right )$.
Tọa độ trọng tâm $G$ của tam giác $ABC$ là: $G\left ( \frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3} \right )$.
Các công thức khác

Vector chỉ phương, vector pháp tuyến

Phương trình tham số của đường thẳng

Phương trình tổng quát của đường thẳng

Phương trình đoạn chắn của đường thẳng

Phương trình đường thẳng và đồ thị hàm bậc nhất
Đồ thị của hàm bậc nhất $y=ax+b$ là đường thẳng đi qua điểm $M(0;b)$ và có hệ số góc là $a$.
$y=ax+b\Leftrightarrow ax-y+b=0$.
Vậy đồ thị của hàm bậc nhất này là đường thẳng có vector pháp tuyến $\overrightarrow{n}=(a;-1)$ và có phương trình tổng quát là $ax-y+b=0$.
Cho đường thẳng $d: ax+by+c=0$ với $a,b$ khác 0.
$ax+by+c=0\Leftrightarrow y=\frac{-a}{b}x+\frac{-c}{b}$.
Vậy, $d$ là đồ thị của hàm bậc nhất $y=\frac{-a}{b}x+\frac{-c}{b}$ với hệ số góc $k=\frac{-a}{b}$.

Vị trí tương đối của 2 đường thẳng
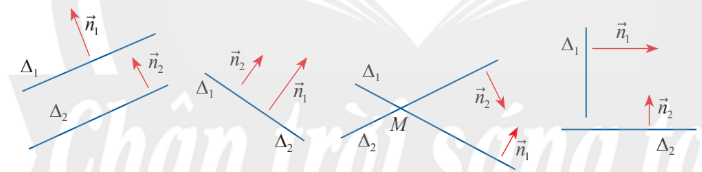


Góc giữa 2 đường thẳng

Góc giữa 2 đường thẳng $\Delta_1,\Delta_2$ được kí hiệu là $(\Delta_1,\Delta_2)$, hoặc $\widehat{(\Delta_1,\Delta_2)}$.
Công thức tính góc giữa 2 đường thẳng
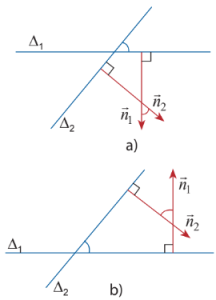
Góc giữa 2 đường thẳng và góc giữa 2 pháp tuyến luôn bằng nhau hoặc bù nhau nên:
$\cos(\Delta_1,\Delta_2)=|\cos(\overrightarrow{n_1},\overrightarrow{n_2})|=\frac{|\overrightarrow{n_1}.\overrightarrow{n_2}|}{|\overrightarrow{n_1}|.|\overrightarrow{n_2}|}$.
Nếu $\overrightarrow{n_1}=(a_1;b_1),\overrightarrow{n_2}=(a_2;b_2)$ thì:
$\cos(\Delta_1,\Delta_2)=\frac{|a_1.a_2+b_1.b_2|}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$
Góc giữa 2 đường thẳng và góc giữa 2 vector chỉ phương luôn bằng nhau hoặc bù nhau nên công thức trên cũng đúng nếu có các vector chỉ phương $\overrightarrow{u_1},\overrightarrow{u_2}$:
$\cos(\Delta_1,\Delta_2)=|\cos(\overrightarrow{u_1},\overrightarrow{u_2})|=…$

Khoảng cách từ 1 điểm đến 1 đường thẳng
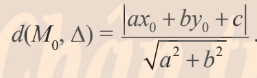
Phương trình đường tròn
Đường tròn tâm $I(a;b)$ bán kính $R$ có phương trình là:
$(x-a)^2+(y-b)^2=R^2$.
Vì $(x-a)^2+(y-b)^2=R^2\Leftrightarrow x^2-2ax+a^2+y^2-2by+b^2-R^2=0$ nên phương trình đường tròn còn có dạng khác là:
$x^2+y^2-2ax-2by+c=0$ với $c=a^2+b^2-R^2$.
Khi đó, $R=\sqrt{a^2+b^2-c}$.
Nên $$x^2+y^2-2ax-2by+c=0$ là phương trình của đường tròn khi và chỉ khi $a^2+b^2-c>0$.
Phương trình tiếp tuyến của đường tròn
Tiếp tuyến của đường tròn tâm $I(a;b)$ tại điểm $M(x_M;y_M)$ sẽ vuông góc với $IM$ nên nó có phương trình là:
$(a-x_M)(x-x_M)+(b-y_M)(y-y_M)=0$
Elip
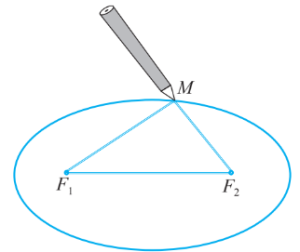

Phương trình chính tắc của elip:
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với $b=\sqrt{a^2-c^2}$.
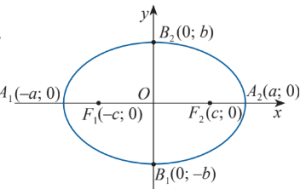
$A_1,A_2,B_1,B_2$ là các đỉnh của elip.
Trục lớn: đoạn thẳng $A_1A_2$.
Trục nhỏ: đoạn thẳng $B_1B_2$.
Tâm đối xứng: $O$.
Điểm $M(x_M;y_M)$ thuộc elip thì: $|x_M|\leq a, |y_M\leq b|$.
Hypebol
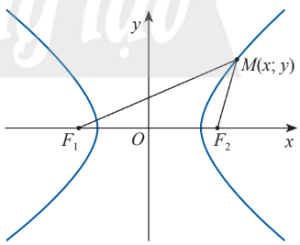

Phương trình chính tắc của hypebol
$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với $b=\sqrt{c^2-a^2}$.
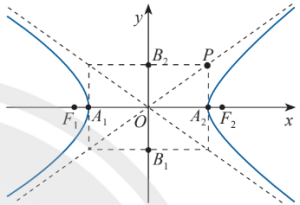
$A_1,A_2$ là các đỉnh của hypebol.
Trục thực là đoạn $A_1A_2$.
Trục ảo là đoạn $B_1B_2$.
Tâm đối xứng: $O$.
Điểm $M(x_M;y_M)$ thuộc hypebol thì: $x_M\leq -a$ hoặc $x_M\geq a$.
Parabol
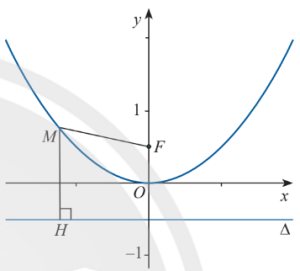

Phương trình chính tắc của parabol
$y^2=2px$.
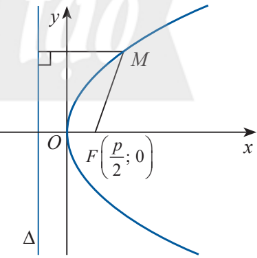
Đỉnh: $O$.
Trục đối xứng: $Ox$.
Tham số tiêu: $p$.
Điểm $M(a;b)$ thuộc parabol thì $a\geq 0$ và có điểm đối xứng là $M'(a;-b)$.
Chương 10.
Phép thử ngẫu nhiên và không gian mẫu
Phép thử ngẫu nhiên (gọi tắt là phép thử) là 1 hoạt động mà ta không thể biết trước được kết quả của nó.
Tập hợp các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu, kí hiệu là $\Omega $.
Biến cố
Mỗi tập hợp con của không gian mẫu được gọi là biến cố, thường được kí hiệu là $A,B,C,…$
Một kết quả thuộc biến cố $A$ được gọi là kết quả làm cho $A$ xảy ra, hoặc kết quả thuận lợi cho $A$.
Biến cố chắc chắn: là biến cố luôn xảy ra, đó chính là $\Omega$.
Biến cố không thể: là biến cố không bao giờ xảy ra, đó chính là tập hợp $\emptyset$.
Xác suất của biến cố
Giả sử 1 phép thử có không gian mẫu $\Omega$ gồm hữu hạn kết quả có cùng khả năng xảy ra, và $A$ là 1 biến cố.
Xác suất của biến cố $A$, kí hiệu là $P(A)$, được xác định như sau:
$P(A)=\frac{n(A)}{n(\Omega)}$ với $n(A),n(\Omega)$ là số phần tử của $A,\Omega$.
Với mọi biến cố $A$ thì $0\leq P(A)\leq 1$.
$P(\Omega)=1,P(\emptyset)=0$.
Xác suất là để đo lường khả năng xảy ra của biến cố. Khả năng xảy ra càng cao thì xác suất càng gần 1.
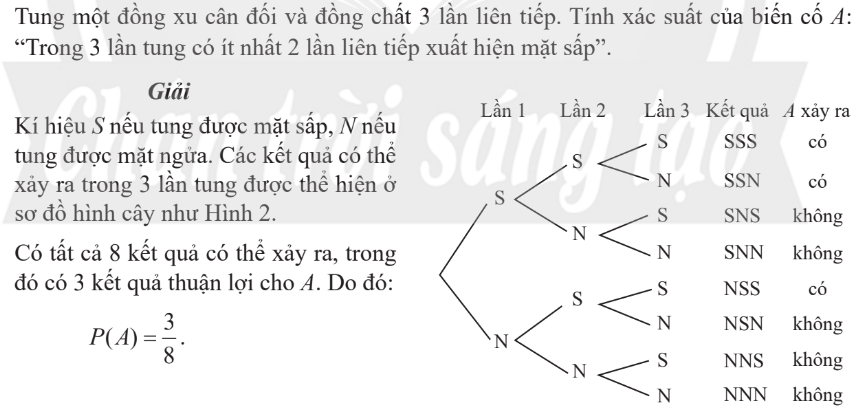
Tính xác suất bằng sơ đồ cây
Biến cố đối
Biến cố đối của $A$, kí hiệu là $\overline{A}$, là biến cố “Không xảy ra $A$”.
Ta có:
- $\overline{A}=\Omega\setminus A$.
- $P(\overline{A})+P(A)=1$.
Nguyên lí xác suất bé
Nếu 1 biến cố có xác suất rất bé thì trong 1 phép thử, biến cố đó sẽ gần như không xảy ra.

