Chương 1.
Dữ liệu
Thống kê được định nghĩa là nghệ thuật và khoa học trong việc thu thập, phân tích, trình bày và diễn giải dữ liệu.
Phần tử: thực thể mà dữ liệu của nó dc thu thập.
Biến: đặc tính của phần tử.
Quan sát: các phép đo cho 1 phần tử.
Số phép đo = số biến Quan sát: bộ số liệu của 1 phần tử. Thang đo:
- danh nghĩa: tên phân loại
- thứ tự: thứ hạng, đánh giá
- khoảng: con số, có thứ tự và khoảng cách, có thể âm
- tỷ lệ: con số, có đặc tính khoảng và tỷ lệ: dưới 1, từ 1 đến 2, lớn hơn 2.
Có 2 loại dữ liệu:
- dữ liệu phân loại: được nhóm theo danh mục cụ thể
- dữ liệu định lượng: giá trị số
Dữ liệu cắt ngang: thu thập gần như cùng thời điểm.
Chuỗi thời gian: dữ liệu thu thập ở nhiều thời điểm.
Dữ liệu định lượng có thể:
- rời rạc: số cuộc gọi trong ngày
- liên tục: trọng lượng, thời gian
Từ tổ chức, hiệp hội, cơ quan chính phủ, internet, khảo sát.
Nghiên cứu thống kê: thử nghiệm hoặc quan sát dữ liệu có sẵn.
Lỗi thu thập dữ liệu: xem xét sự bất thường (ngoại lệ)
Là dạng tóm tắt dữ liệu thành bảng, đồ thị để người đọc dễ hiểu.
Dân số: nhóm phần tử lớn (có thể là tất cả)
Mẫu: nhóm nhỏ phần tử trong dân số.
Điều tra dân số: thu thập dữ liệu cho toàn bộ dân số.
Khảo sát mẫu: thu thập dữ liệu cho 1 mẫu.
Minitab, excel, statools.
Ra quyết định từ cơ sở dữ liệu lớn. Dựa chủ yếu vào:
- hồi quy bội
- hồi quy logistic
- tương quan
Đánh giá độ tin cậy của mô hình: chia dữ liệu mẫu thành 2 phần
- huấn luyện
- thử nghiệm
Nếu dữ liệu huấn luyện dự đoán chính xác giá trị trong dữ liệu thử nghiệm thì mô hình là đáng tin cậy.
Sai trong:
- lấy mẫu
- phân tích
- tóm tắt
- diễn giải
Chương 2.
Phân bố tần số: tóm tắt dữ liệu dạng bảng hiển thị tần số các mục.
Tần suất = tần số / n
Tần suất phần trăm = tần suất * 100 (%)
Biểu đồ thanh và biểu đồ tròn.
Các nhóm có tần suất dưới 5% thường được gom chung thành 1 nhóm: Khác
3 bước xác định các lớp :
- ko chồng chéo
- chiều rộng lớp = (số liệu lớn nhất – số liệu nhỏ nhất) / số lớp
- giới hạn lớp: ví dụ: 10-14, 15-19, 20-24. Khoảng cách giữa giới hạn dưới và giới hạn trên bằng độ rộng lớp.
Nên sử dụng từ 5 đến 20 lớp.
Điểm giữa của lớp = (giới hạn dưới + giới hạn trên) / 2
Biểu đồ chấm (dot plot)
Phân phối tần số tích lũy: số dữ liệu nhỏ hơn hoặc bằng giới hạn trên.
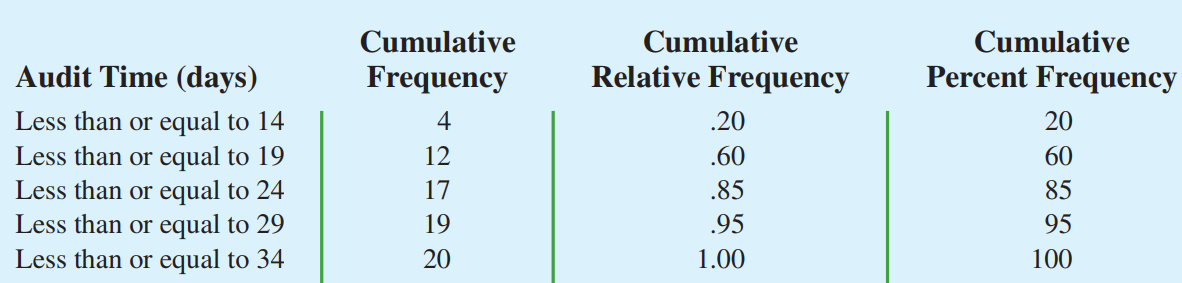
Histogram:
Biểu đồ phân phối tích lũy: ogive.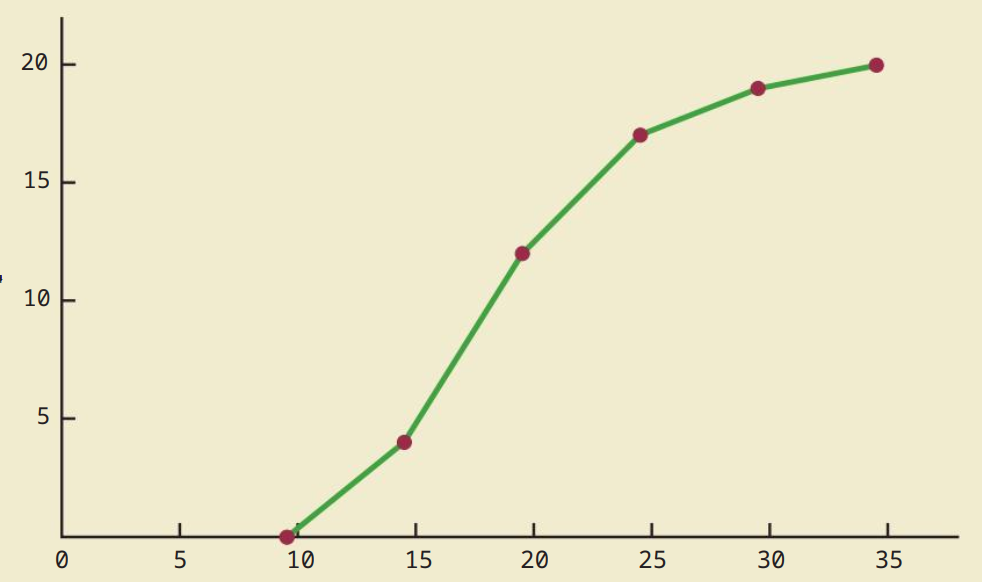 
Từ dữ liệu: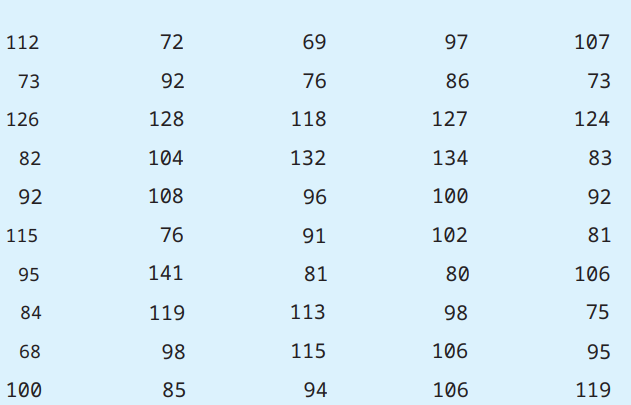 
Hiển thị thân và lá: (bên trái là thân, bên phải là lá) 
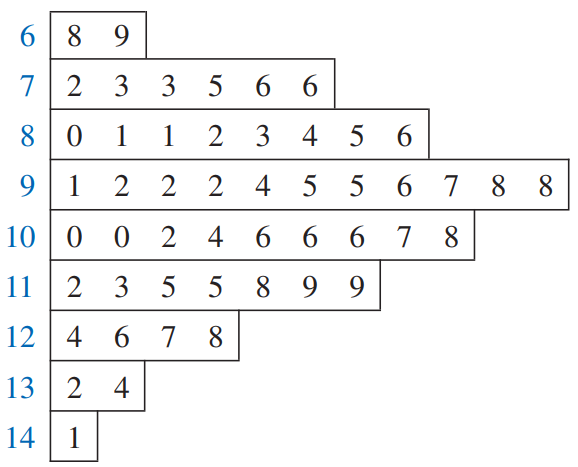Dòng đầu thể hiện số 68,69. Dòng cuối thể hiện số 141. 2 Dòng đầu thay cho các lớp: 60-69, 70-79.
Chú ý phần lá: có 1 chữ số.
Bảng chéo: bảng dữ liệu 2 biến.
Nghịch lý Simpson: sự đảo ngược kết luận sau khi tổng hợp dữ liệu.
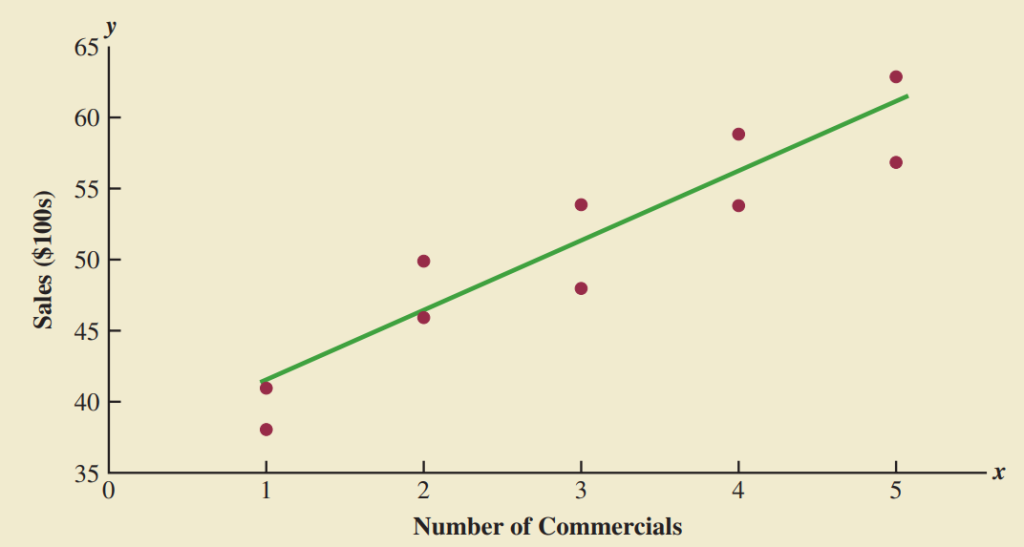
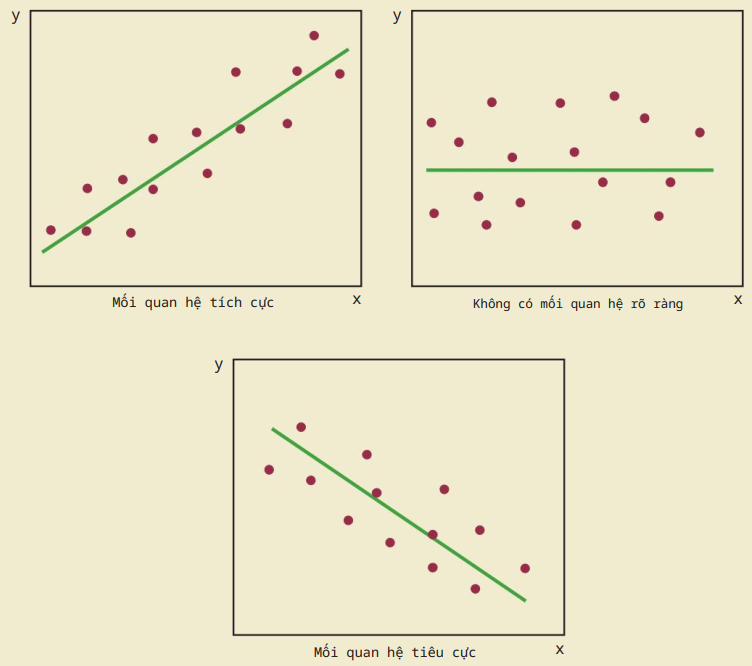
Biểu đồ phân tán: mối quan hệ giữa 2 biến định lượng.
Đường xu hướng: mối quan hệ.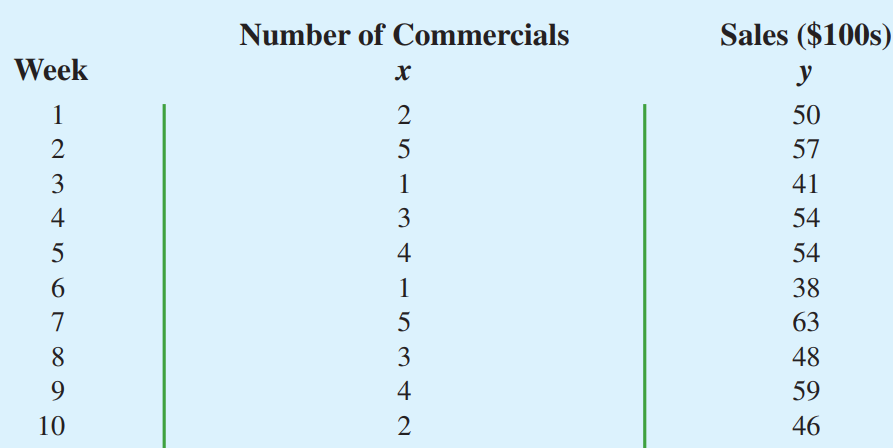 
Dùng Excel:
- hàm countif tạo bảng tần số
- biểu đồ thanh
- bảng pivot tạo bảng tần số ghép lớp (group) và biểu đồ tần số %, tạo bảng chéo
- biểu đồ phân tán, đường xu hướng
- biểu đồ thống kê (histogram)
Chương 3.
Giá trị trung bình – mean
- của mẫu: $\overline{x}= \frac{\sum x_i}{n}$
- của tổng thể: $\mu= \frac{\sum x_i}{N}$
Trung vị – median: là giá trị ở giữa (hoặc trung bình cộng của 2 giá trị ở giữa) sau khi dữ liệu được sắp xếp.
Mode: là dữ liệu có tần số lớn nhất.
Bimodal: có 2 mode
Multimodal: số mode lớn hơn 2
Phân vị thứ p – percentile: là giá trị phân chia dữ liệu đã sắp xếp thành 2 phần:
- phần giá trị nhỏ hơn: p % và
- phần còn lại: (100 – p) %
3 bước tính phân vị thứ p:
- sắp xếp dữ liệu
- tính $i=\frac{p}{100}.n$
- nếu $i$ ko nguyên thì lấy số nguyên kế nó là số chỉ vị trí, nếu $i$ nguyên thì phân vị thứ p bằng trung bình cộng giá trị thứ $i$ và $i+1$.
Phân vị thứ 50 cũng là trung vị.
Tứ phân vị: chia dữ liệu thành 4 phần, mỗi phần chiếm 25% số quan sát
- Q1: tứ phân vị thứ nhất – phân vị thứ 25
- Q2: tứ phân vị thứ 2 – phân vị thứ 50
- Q3: tứ phân vị thứ 3 – phân vị thứ 75
Phạm vi = max – min
Phạm vi tứ phân vị: IQR = Q3 – Q1
Phương sai: chênh lệch giữa giá trị quan sát và giá trị trung bình
$\sigma^2=\frac{\sum (x_i-\mu)^2}{N}$
Phương sai mẫu: $s^2=\frac{\sum (x_i-\overline{x})^2}{n-1}$
Công thức thay thế: $s^2=\frac{\sum x_i^2 – n.\overline{x}^2}{n-1}$
Độ lệch chuẩn: $\sigma$
Độ lệch chuẩn mẫu: $s$
Hệ số biến thiên: coeficienct of variation = $\frac{\sigma}{\mu}.100$ %
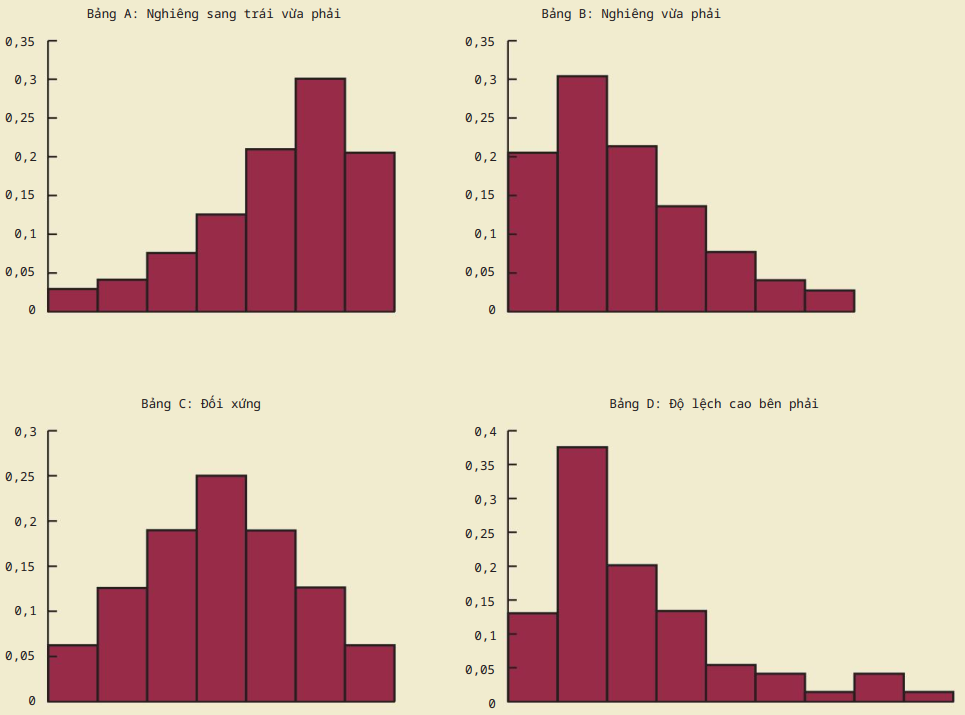
Thước đo hình dạng
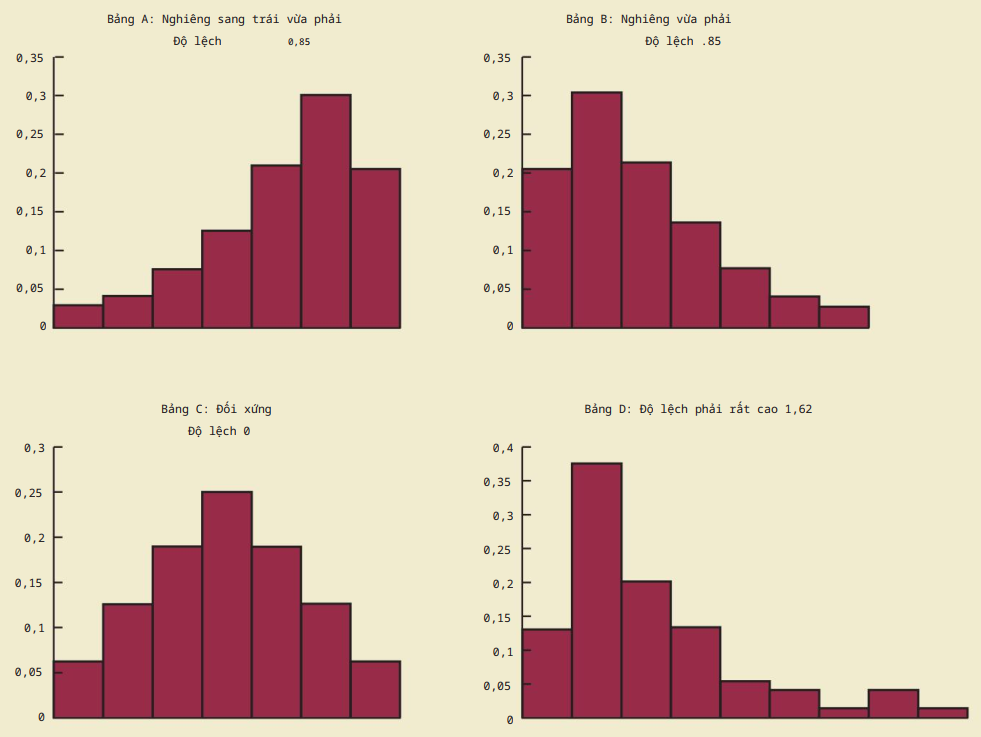
Độ lệch mẫu – skewness = $\frac{n}{(n-1)(n-2)}\sum \left ( \frac{x_i – \overline{x}}{s} \right )^3$
- âm – lệch trái
- dương – lệch phải
- 0 – đối xứng
Khi dữ liệu có sự chênh lệch lớn thì trung vị là thước đo thích hợp hơn trung bình.
Thước đo vị trí tương đối so với trung bình
Z-score: $z_i=\frac{x_i – \overline{x}}{s}$
Định lý Chebyshev:
Cho số $z>1$, có ít nhất $1-\frac{1}{z^2}$ giá trị dữ liệu nằm trong $z$ lần độ lệch chuẩn.
Quy tắc thực nghiệm
Đối với dữ liệu hình chuông:
- 68% dữ liệu nằm trong khoảng 1 lần độ lệch chuẩn so với mean
- 95% dữ liệu nằm trong khoảng 2 lần độ lệch chuẩn so với mean
- hầu hết dữ liệu nằm trong khoảng 3 lần độ lệch chuẩn so với mean
Phát hiện ngoại lệ
Giá trị ngoại lệ là kiểu:
- bất thường: khi |z-scores| lớn hơn3
- không chính xác
Tóm tắt 5 số
- giá trị nhỏ nhất
- $Q_1$
- $Q_2$
- $Q_3$
- giá trị lớn nhất
Biểu đồ hộp
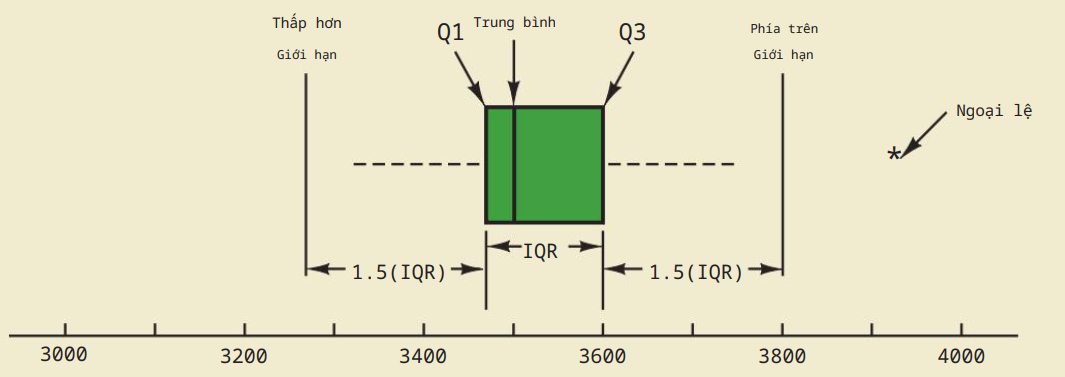
Cách vẽ:
- Tính $Q_1,Q_3$ để xác định đỉnh và đáy hộp.
- Tính median để xác định đường giữa hộp.
- Tính $IQR=Q_3-Q1$. Giới hạn trái bằng $Q_1-1,5IQR$. Giới hạn phải bằng $Q_3+1,5IQR$. Bên ngoài 2 giới hạn này là ngoại lệ.
- Đường nét đứt trên hình gọi là râu, kéo dài đến các giá trị nhỏ nhất và lớn nhất nằm trong 2 giới hạn tính ở bước trên.
- Các giá trị ngoại lệ được hiển thị bằng dấu “*”.
Hiệp phương sai
Là thước đo mối quan hệ tuyến tính giữa 2 biến.
Hiệp phương sai mẫu: $s_{xy}=\frac{\sum (x_i-\overline{x})(y_i-\mu _y)}{n-1}$
Hiệp phương sai tổng thể: $\sigma_{xy}=\frac{\sum (x_i-\mu_x)(y_i-\mu_y)}{N}$
Giải thích hiệp phương sai
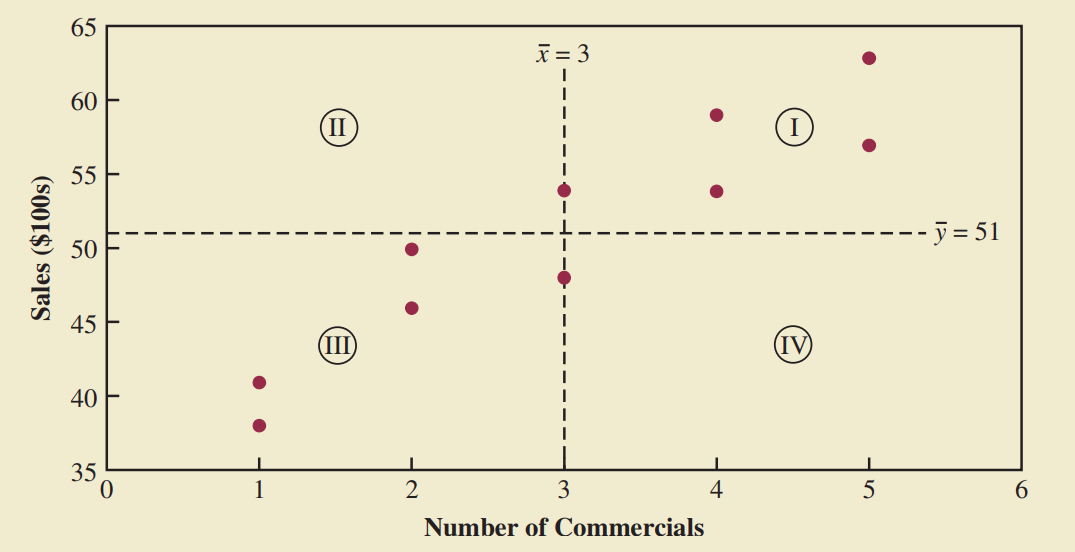
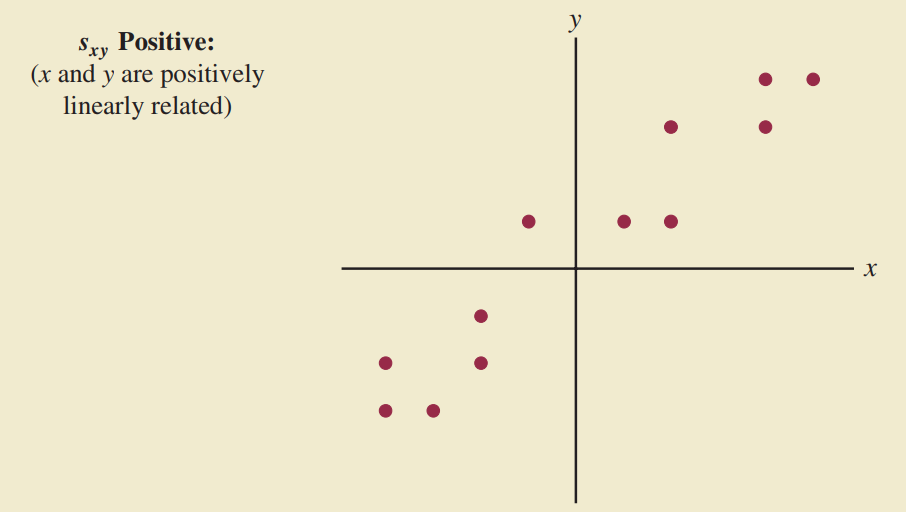
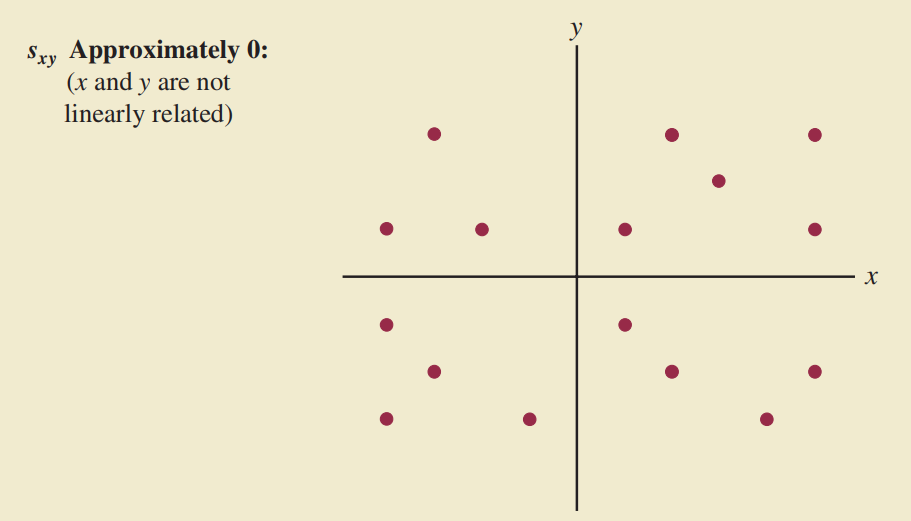
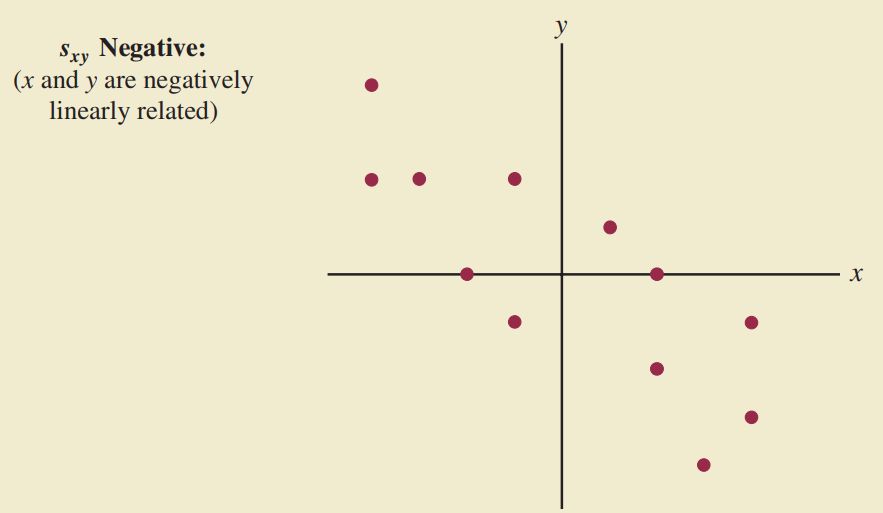
Giá trị của hiệp phương sai phụ thuộc vào đơn vị đo của $x,y$.
Để loại bỏ ảnh hưởng của đơn vị đo, ta sẽ dùng:
Hệ số tương quan
Hệ số tương quan mẫu: $r_{xy}=\frac{s_{xy}}{s_x.s_y}$ với $s_x,s_y$ là các độ lệch chuẩn.
Hệ số tương quan tổng thể: $\rho_{xy}=\frac{\sigma_{xy}}{\sigma_x.\sigma_y}$.
$r_{xy}$ càng gần 1 thì mối quan hệ tuyến tính càng mạnh, càng gần 0 thì càng yếu.
Trung bình có trọng số
$\overline{x}=\frac{\sum w_ix_i}{\sum w_i} $
Dữ liệu nhóm
Trung bình mẫu cho dữ liệu nhóm: $\overline{x}=\frac{\sum f_iM_i}{n} $ với $M_i$ là trung điểm của lớp $i$.
Phương sai mẫu cho dữ liệu nhóm: $s^2=\frac{\sum f_i(M_i-\overline{x})^2}{n-1}$
Trung bình và phương sai tổng thể cũng được tính tương tự.
Chương 4.
| Thí nghiệm | Kết quả thí nghiệm |
| tung đồng xu | xấp, ngửa |
| chọn 1 cái để kiểm tra | lỗi, không lỗi |
| gọi điện bán hàng | mua, không mua |
| đổ xúc xắc | 1,2,3,4,5,6 |
| chơi 1 trận bóng đá | thắng, thua, hòa |
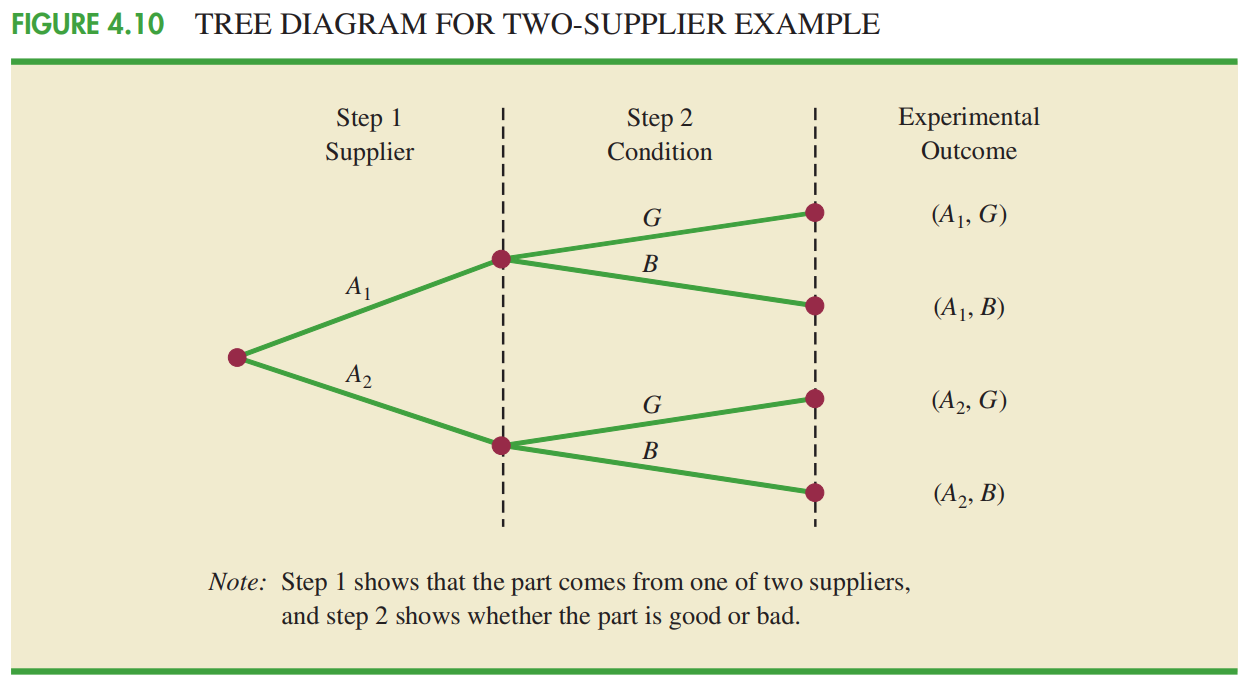
Không gian mẫu: là tập hợp tất cả các kết quả của phép thử.
Điểm mẫu: là 1 kết quả thực nghiệm.
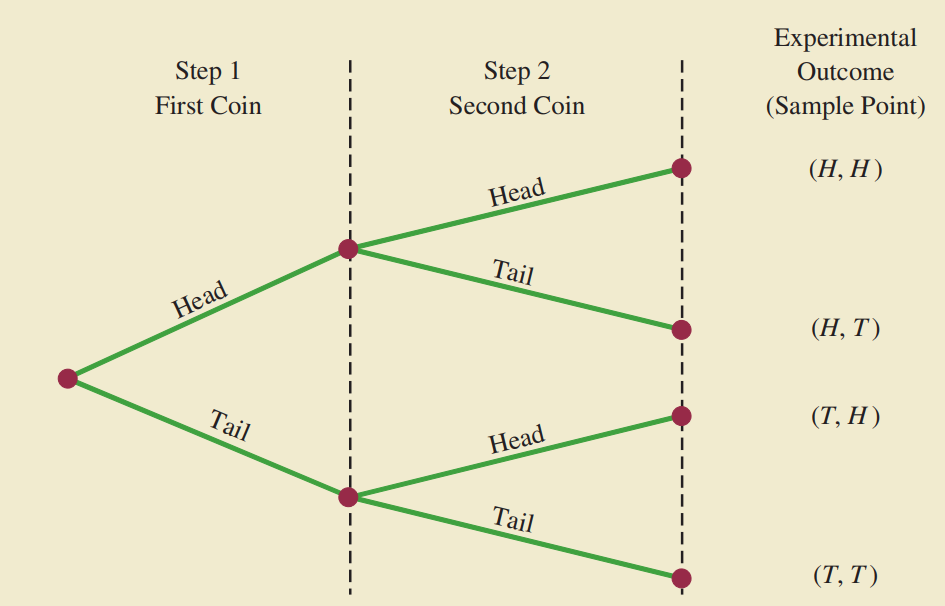
Quy tắc đếm nhiều bước
(Quy tắc nhân)
Tổ hợp
$C^N_n$
Hoán vị lấy $n$ đối tượng
(Chỉnh hợp)
$P^N_n$
Gán xác suất
3 phương pháp:
- Cổ điển: khi các kết quả thực nghiệm có khả năng xảy ra như nhau
- Tần số tương đối: khi có sẵn dữ liệu để ước tính tỷ lệ số lần mà kết quả thực nghiệm sẽ xảy ra nếu thí nghiệm được lặp lại với số lần lớn
- Chủ quan: khi người ta không thể giả định một cách thực tế rằng các kết quả thực nghiệm có khả năng xảy ra như nhau và khi có ít dữ liệu liên quan. Khi phương pháp chủ quan được sử dụng để gán xác suất cho các kết quả thử nghiệm, chúng tôi có thể sử dụng bất kỳ thông tin nào có sẵn, chẳng hạn như kinh nghiệm hoặc trực giác của chúng tôi. Sau khi xem xét tất cả các thông tin có sẵn, một giá trị xác suất thể hiện mức độ tin tưởng của chúng ta (theo thang điểm từ 0 đến 1) rằng kết quả thử nghiệm sẽ xảy ra sẽ được chỉ định. Bởi vì xác suất chủ quan thể hiện mức độ tin tưởng của một người nên nó mang tính cá nhân. Bằng cách sử dụng phương pháp chủ quan, những người khác nhau có thể sẽ gán những xác suất khác nhau cho cùng một kết quả thí nghiệm.
2 yêu cầu cơ bản để ấn định xác suất:
- Nếu $E_i$ là kết quả thí nghiệm thứ $i$ thì $0\leq P(E_i)\leq 1$
- Khi thực nghiệm có $n$ kết quả thì $P(E_1)+P(E_2)+…+P(E_n)=1$
Sự kiện là tập hợp 1 số kết quả thí nghiệm.
Xác suất của 1 sự kiện bằng tổng xác suất các kết quả của nó.
Phần bù của A: là các kết quả không thuộc sự kiện A, kí hiệu là $A^C$.
$P(A)+P(A^C)=1.
Luật bổ sung
Hợp 2 sự kiện: $A\cup B$.
Giao 2 sự kiện: $A\cap B$.
$P(A\cup B)=P(A)+P(B)-P(A\cap B)$.
2 sự kiện xung khắc: không có chung điểm mẫu.
Nếu A,B xung khắc thì $P(A\cap B)=0$. Lúc đó: $P(A\cup B)=P(A)+P(B)$.
Giả sử chúng ta có một sự kiện A với xác suất P(A). Nếu chúng ta có được thông tin mới và tìm hiểu rằng một sự kiện liên quan, ký hiệu là B, đã xảy ra, chúng ta sẽ muốn tận dụng điều này bằng cách tính toán xác suất mới cho sự kiện A. Xác suất mới này của sự kiện A được gọi là xác suất có điều kiện và được viết là P(A | B).
$P(A|B)=\frac{P(AB)}{P(B)}$.
$P(B|A)=\frac{P(AB)}{P(A)}$.
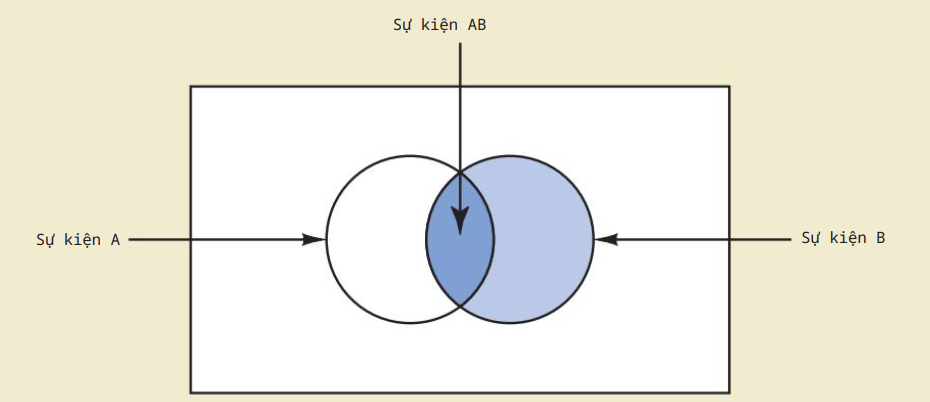
Sự kiện độc lập
Khi $P(A|B)\not= P(A)$, ta nói $A,B$ là các sự kiện phụ thuộc. Tức là xác suất của $A$ bị ảnh hưởng khi $B$ tồn tại.
Khi $P(A|B)= P(A)$, ta nói $A,B$ là các sự kiện độc lập. Tức là xác suất của $A$ không bị ảnh hưởng khi $B$ tồn tại.
Lúc đó, ta cũng có $P(B|A)=P(B)$.
Do $P(A|B)=\frac{P(AB)}{P(B)}$ nên khi đó $P(A)=\frac{P(AB)}{P(B)}$. Suy ra $P(AB)=P(A).P(B)$.
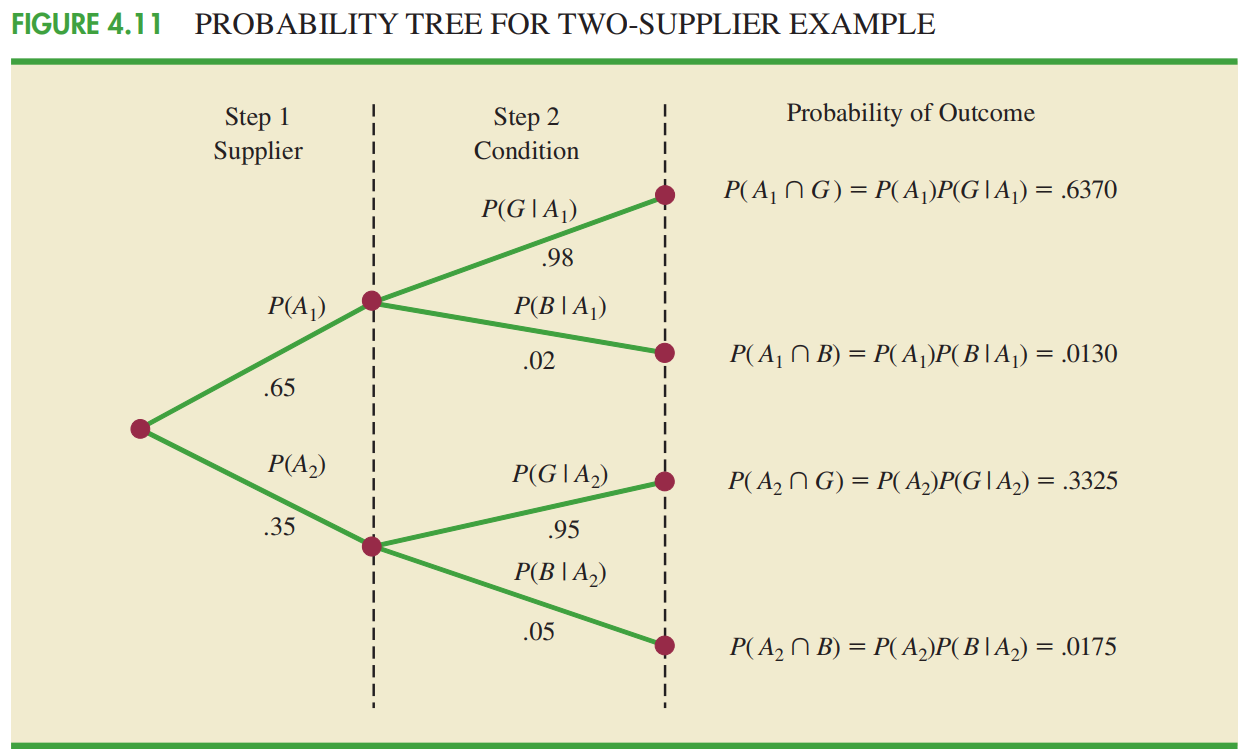
Luật nhân
$P(AB)=P(B).P(A|B)=P(A).P(B|A)$.
Nếu $A,B$ độc lập thì $P(AB)=P(A).P(B)$.
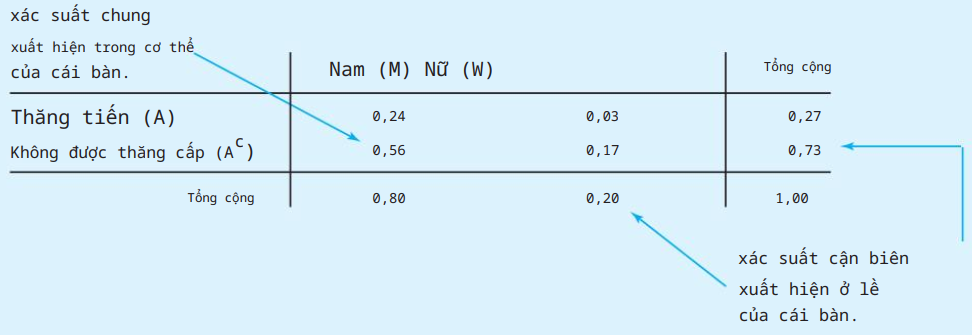
Định lý Bayes có thể áp dụng được khi các sự kiện mà chúng ta muốn tính xác suất hậu nghiệm loại trừ lẫn nhau và hợp của chúng là toàn bộ không gian mẫu.
Với 2 sự kiện:
$P(A_1|B)=\frac{P(A_1).P(B|A_1)}{P(A_1).P(B|A_1)+P(A_2).P(B|A_2)}$.
$P(A_2|B)=\frac{P(A_2).P(B|A_2)}{P(A_1).P(B|A_1)+P(A_2).P(B|A_2)}$.
Với $n$ sự kiện:
$P(A_i|B)=\frac{P(A_i).P(B|A_i)}{P(A_1).P(B|A_1)+P(A_2).P(B|A_2)+…+P(A_n).P(B|A_n)}$.
Cách tiếp cận dạng bảng
Chương 5.
Trọng tâm của chương này là phân bố xác suất rời rạc.
3 phân bố xác suất rời rạc đặc biệt:
- phân bố nhị thức
- Poisson
- siêu hình học
Một biến ngẫu nhiên cung cấp một phương tiện để mô tả kết quả thử nghiệm bằng cách sử dụng các giá trị số. Các biến ngẫu nhiên phải có giá trị số.
Một biến ngẫu nhiên có thể có số lượng giá trị hữu hạn hoặc một chuỗi vô hạn của các giá trị như 0, 1, 2, . . . được gọi là biến ngẫu nhiên rời rạc.
Một biến ngẫu nhiên có thể nhận bất kỳ giá trị số nào trong một khoảng hoặc tập hợp các khoảng được gọi là biến ngẫu nhiên liên tục. Kết quả thí nghiệm dựa trên các thang đo đo lường như thời gian, trọng lượng, khoảng cách và nhiệt độ có thể được mô tả bằng biến ngẫu nhiên liên tục.
Phân phối xác suất cho một biến ngẫu nhiên mô tả cách phân phối xác suất trên các giá trị của biến ngẫu nhiên. Đối với biến ngẫu nhiên rời rạc x, phân bố xác suất được xác định bởi hàm xác suất, ký hiệu là f(x). Hàm xác suất cung cấp xác suất cho từng giá trị của biến ngẫu nhiên.
2 điều kiện bắt buộc đối với hàm xác suất rời rạc:
- $f(x)\geq 0$
- $\sum f(x)=1$
Một công thức cung cấp hàm xác suất f(x) cho mọi giá trị của x thường được sử dụng để mô tả phân bố xác suất.
Ví dụ đơn giản nhất của phân bố xác suất rời rạc được cho bởi một công thức là xác suất đồng đều rời rạc: $f(x)=\frac{1}{n}$ với $n$ là số giá trị mà biến ngẫu nhiên $x$ có thể nhận.
Giá trị kỳ vọng hoặc giá trị trung bình của một biến ngẫu nhiên là thước đo vị trí trung tâm của biến ngẫu nhiên. biến ngẫu nhiên. Công thức tính giá trị kỳ vọng của biến ngẫu nhiên rời rạc x như sau: $E(x)=\mu =\sum xf(x)$.
Công thức tính phương sai của biến ngẫu nhiên rời rạc: $Var(x)=\sigma ^2=\sum (x-\mu )^2f(x)$
Một thí nghiệm nhị thức có 4 đặc điểm:
- có n lần thử giống nhau
- mỗi lần thử có 2 kết quả: thành công, thất bại
- xác suất thành công, p, và xác suất thất bại, 1-p, là không đổi qua các lần thử
- các thử nghiệm là độc lập
Quy trình Bernoully: có các đặc tính 2,3,4 ở trên.
Hàm xác suất nhị thức:
$f(x)=\left ( ^n_x \right )p^x(1-p)^{n-x}$
với $x$ là số lần thành công,
$p$ là xác suất thành công trong 1 lần thử,
$n$ là số lần thử,
$\left ( ^n_x \right )=\frac{n!}{x!.(n-x)!}$.
Kỳ vọng: $E(x)=n.p$
Phương sai: $Var(x)=np(1-p)$
2 đặc điểm của thử nghiệm Poisson:
- xác suất xảy ra là như nhau với 2 khoảng thời gian dài như nhau.
- việc xảy ra trong khoảng thời gian này độc lập với khoảng thời gian khác.
Hàm xác suất Poisson:
$f(x)=\frac{\mu^xe^{-\mu}}{x!}$
với $x$ là số lần xuất hiện trong 1 khoảng,
$\mu$ là kỳ vọng hoặc trung bình số lần xuất hiện trung bình trong 1 khoảng,
$e\approx 2,7$.
$x$ càng lớn thì $f(x)$ càng gần 0.
Phương sai: $Var(x)=\mu$.
Khi tính xác suất Poisson cho một khoảng thời gian khác, trước tiên chúng ta phải chuyển đổi tốc độ đến trung bình thành khoảng thời gian quan tâm và sau đó tính xác suất.
Trong $N$ phần tử có $r$ phần tử được xem là thành công, còn lại $N-r$ là thất bại.
Lấy ra $n$ phần tử, trong đó có $x$ thành công, còn lại $n-x$ là thất bại.
Hàm xác suất siêu hình học là:
$f(x)=\frac{\left ( ^r_x \right ).\left ( ^{N-r}_{n-x} \right )}{\left ( ^N_n \right )}$.
Kỳ vọng: $E(x)=\mu=n.\frac{r}{N}$.
Phương sai: $Var(x)=n.\frac{r}{N}.\left ( 1-\frac{r}{N} \right ).\frac{N-n}{N-1}$.
Khi $N$ lớn thì phân phối siêu bội gần như là phân phối nhị thức với $p=r/N$.
Chương 6.
Chương này mở rộng thảo luận về phân bố xác suất cho trường hợp các biến ngẫu nhiên liên tục. Sự khác biệt chính về mặt khái niệm giữa phân bố xác suất rời rạc và liên tục liên quan đến phương pháp tính xác suất. Với phân bố rời rạc, hàm xác suất f(x) cung cấp xác suất để biến ngẫu nhiên x nhận các giá trị khác nhau. Với phân bố liên tục, hàm mật độ xác suất f(x) không cung cấp trực tiếp các giá trị xác suất. Thay vào đó, xác suất được cho bởi diện tích dưới đường cong hoặc đồ thị của hàm mật độ xác suất f(x). Vì diện tích dưới đường cong phía trên một điểm bằng 0 nên chúng ta quan sát thấy xác suất của bất kỳ giá trị cụ thể nào cũng bằng 0 đối với một biến ngẫu nhiên liên tục.
Hàm mật độ của phân phối đều:
$f(x)=\left\{\begin{matrix}
\frac{1}{b-a} & ,x\in[a;b]\\
0 & ,x\notin [a;b]
\end{matrix}\right.$
Xác suất là diện tích bên dưới $f(x$.
Kỳ vọng: $E(x)=\frac{a+b}{2}$.
Phương sai: $Var(x)=\frac{(b-a)^2}{12}$
Hàm mật độ của phân phối chuẩn:
$f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-(x-\mu)^2/2\sigma^2}$
với $\mu$ là trung bình, $\sigma$ là độ lệch chuẩn.
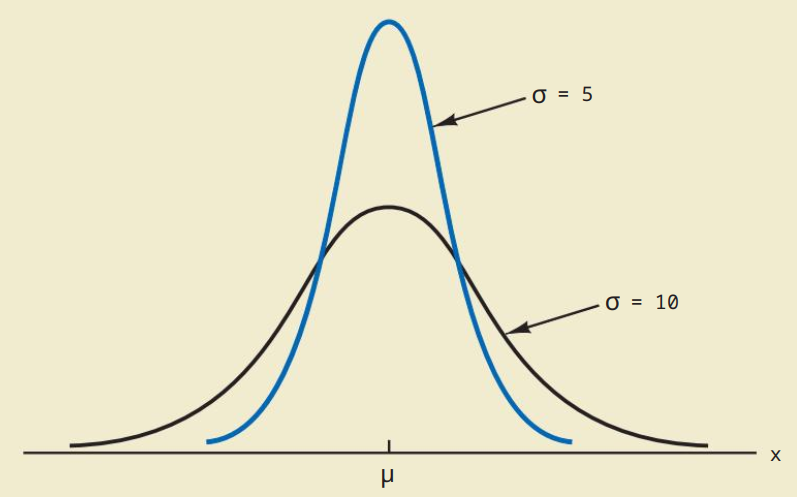
Tỷ lệ phần trăm của các giá trị trong một số khoảng thường được sử dụng là
- a. 68,3% giá trị của một biến ngẫu nhiên thông thường nằm trong khoảng cộng hoặc trừ một độ lệch chuẩn so với giá trị trung bình của nó.
- b. 95,4% giá trị của một biến ngẫu nhiên thông thường nằm trong khoảng cộng hoặc trừ hai độ lệch chuẩn so với giá trị trung bình của nó.
- c. 99,7% giá trị của một biến ngẫu nhiên thông thường nằm trong khoảng cộng hoặc trừ ba độ lệch chuẩn so với giá trị trung bình của nó.
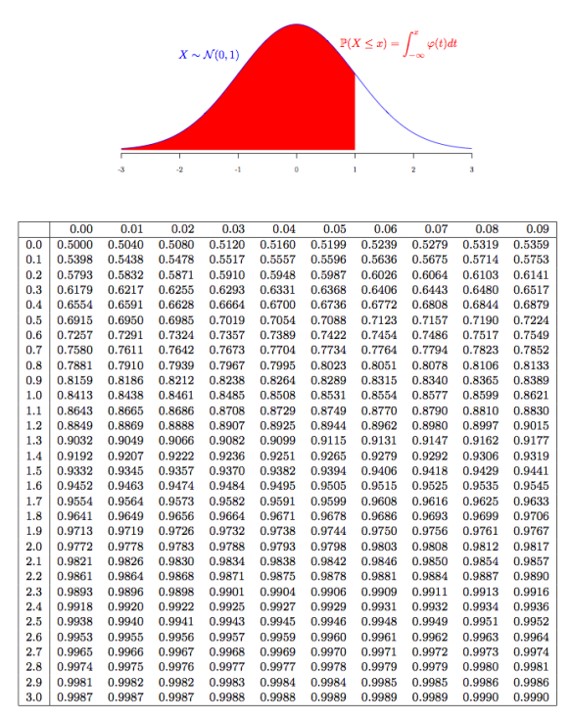
Phân phối chuẩn tắc: có $\mu=0,\sigma=1$
Hàm mật độ của phân phối chuẩn tắc:
$f(x)=\frac{1}{ \sqrt{2\pi}}e^{-x^2/2}$.
Cho biến ngẫu nhiên $x$ có phân phối chuẩn.
Khi đó $z=\frac{x-\mu}{\sigma}$ có phân phối chuẩn tắc
Khi phân phối nhị thức có $np\geq 5$ và $n(1-p)\geq 5$, ta có thể xấp xỉ nó bằng phân phối chuẩn với $\mu =np,\sigma=\sqrt{np(1-p)}$
Dùng cho các biến ngẫu nhiên là thời gian giữa các lần đến.
Hàm mật độ: $f(x)=\frac{1}{\mu}e^{-x/\mu}$.
Xác suất: $P(x\leq a)=1-e^{-a/\mu}$
Chương 7.
Có 2 cách:
- lấy mẫu không thay thế: mỗi phần tử được chọn 1 lần
- lấy mẫu có thay thế
Mẫu ngẫu nhiên đơn giản có kích thước n từ một quần thể có kích thước hữu hạn là mẫu được chọn sao cho mỗi mẫu có thể có kích thước n có cùng xác suất được chọn.
Một mẫu ngẫu nhiên có kích thước n từ một quần thể vô hạn là mẫu được chọn sao cho thỏa mãn các điều kiện sau.
- Mỗi phần tử được chọn đều đến từ cùng một quần thể.
- Mỗi phần tử được chọn độc lập.
Công cụ ước lượng điểm: tính toán trên mẫu rồi suy luận về tổng thể.
Biến ngẫu nhiên là một mô tả bằng số về kết quả của một thí nghiệm. Nếu chúng ta coi quá trình chọn một mẫu ngẫu nhiên đơn giản là một thử nghiệm thì giá trị trung bình của mẫu là mô tả bằng số về kết quả của thử nghiệm. Vì vậy, giá trị trung bình mẫu, độ lệch chuẩn và phân bố xác suất là các biến ngẫu nhiên.
$E(\overline{x})=\mu$.
Khi giá trị kỳ vọng của một công cụ ước tính điểm bằng với tham số tổng thể, chúng ta nói rằng công cụ ước tính điểm là không chệch.
Độ lệch chuẩn của $\overline{x}$:
- tổng thể hữu hạn: $\sigma_{\overline{x}}=\sqrt{\frac{N-n}{N-1}}.\frac{\sigma}{\sqrt{n}}$
- tổng thể vô hạn: $\sigma_{\overline{x}}=\frac{\sigma}{\sqrt{n}}$
$\sqrt{\frac{N-n}{N-1}}$ là hệ số hiệu chỉnh tổng thể hữu hạn.
Khi tổng thể quá lớn so với cỡ mẫu thì hệ số này gần bằng 1.
Khi cỡ mẫu nhỏ hơn hoặc bằng 5% tổng thể, ta coi hệ số này bằng 1.
$\sigma_{\overline{x}}$: à sai số chuẩn của giá trị trung bình.
Khi tổng thể có phân phối chuẩn thì trung bình mẫu cũng có phân phối chuẩn.
Khi tổng thể không có phân phối chuẩn, ta dùng định lý sau:
Định lý giới hạn trung tâm:
Phân bố mẫu của trung bình mẫu xấp xỉ phân phối chuẩn khi cỡ mẫu trở nên lớn.
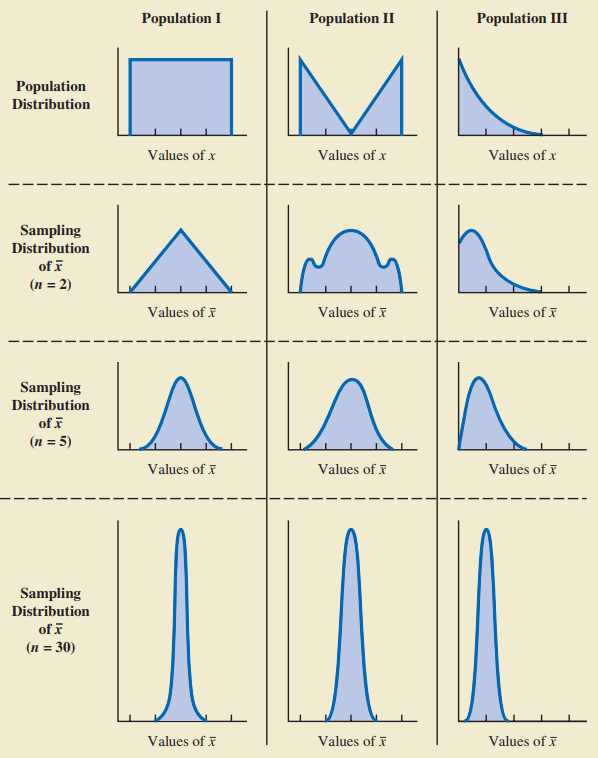
Để phân phối mẫu xấp xỉ phân phối chuẩn, ta thường lấy cỡ mẫu từ 30 trở lên.
Khi tổng thể có độ lệch cao hoặc xuất hiện ngoại lệ, ta lấy cỡ mẫu là 50.
Quan hệ giữa cỡ mẫu và phân phối mẫu:
Cỡ mẫu tăng thì sai số chuẩn của giá trị trung bình giảm. Nên xác suất để trung bình mẫu nằm gần trung bình tổng thể sẽ cao hơn.
Tỷ lệ mẫu: $\overline{p}=x/n$.
$E(\overline{p})=p$
Độ lệch chuẩn của $\overline{p}$:
- nếu tổng thể hữu hạn: $\sigma_{\overline{p}}=\sqrt{\frac{N-n}{N-1}}.\sqrt{\frac{p(1-p)}{n}}$
- nếu tổng thể vô hạn: $\sigma_{\overline{p}}=\sqrt{\frac{p(1-p)}{n}}$
$\overline{p}$ có phân phối nhị thức.
$\overline{p}$ xấp xỉ phân phối chuẩn khi: $np\geq 5$ và $n(1-p)\geq 5$.
3 đặc tính của công cụ ước tính điểm tốt:
- không chệch,
- hiệu quả,
- nhất quán.
$\theta $: tham số của tổng thể
$\widehat{\theta }$: ước lượng điểm của $\theta $.
Không chệch:
$E(\widehat{\theta })=\theta$
Ước lượng hiệu quả:
là công cụ ước lượng điểm nào mà có sai số chuẩn nhỏ hơn.
Nhất quán:
là công cụ ước lượng điểm có xu hướng gần với tham số tổng thể khi cỡ mẫu tăng.
Lấy mẫu ngẫu nhiên phân tầng: khi phương sai trong mỗi tầng nhỏ
chia tổng thể thành các tầng, rồi lấy mẫu từ mỗi tầng.
Lấy mẫu cụm: khi mỗi cụm đại diện quy mô nhỏ cho tổng thể
chia tổng thể thành các cụm, rồi lấy mẫu ngẫu nhiên đơn giản của mỗi cụm.
Lấy mẫu có hệ thống
Lấy mẫu thuận tiện
Lấy mẫu phán đoán
Chương 8.
Khoảng ước lượng: ước lượng điểm $\pm$ biên độ sai số
Độ tin cậy = Hệ số tin cậy (ví dụ 95%).
Khoảng ước lượng cho trung bình:
$\overline{x}\pm z_{\alpha /2}.\frac{\sigma}{\sqrt{n}}$
$1-\alpha$ là độ tin cậy,
$z_{\alpha /2}$ là giá trị sao cho $1-\alpha /2 = P(x<z_{\alpha /2})$.
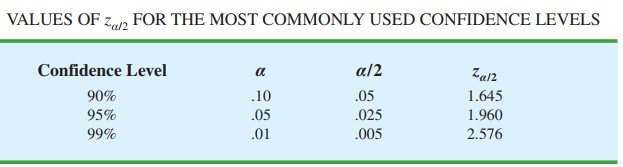
Thông thường, cỡ mẫu n=30 là đủ để sử dụng khoảng ước lượng trên.
Nếu tổng thể phân bổ gần như đối xứng, cỡ mẫu 15 có thể cung cấp khoảng tin cậy đủ tốt.
Khi cỡ mẫu nhỏ hơn, nhà phân tích cần tin tưởng hoặc sẵn sàng giả định phân bố tổng thể gần chuẩn.
Sử dụng phân phối $t$ với 1 tham số gọi là bậc tự do.
Khi bậc tự do tăng lên (hơn 100), phân phối $t$ càng gần phân phối chuẩn.
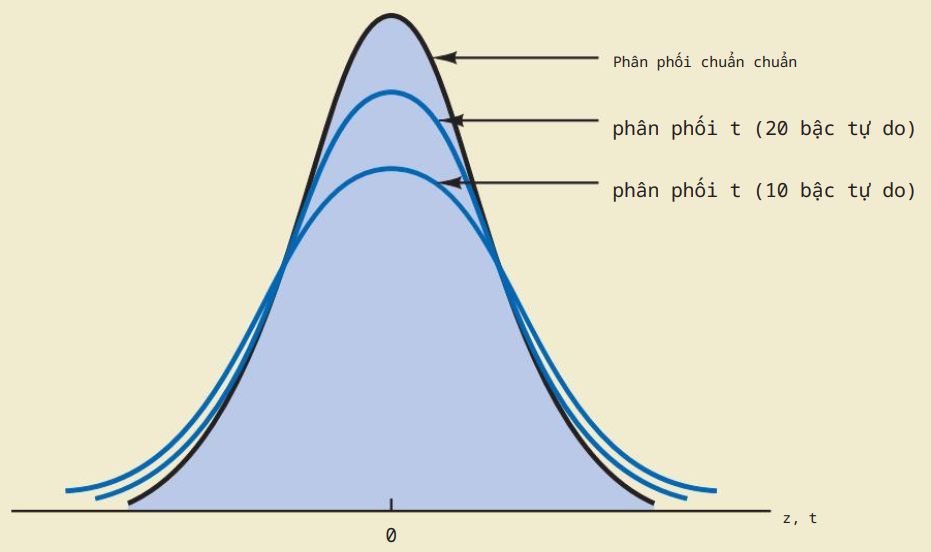
Khi $\sigma$ chưa biết, độ lệch chuẩn mẫu được dùng để ước lượng $\sigma$, $z_{\alpha /2}$ được thay bằng $t_{\alpha /2}$ với bậc tự do là $n-1$.
Độ lệch chuẩn mẫu: $s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}$.
Khoảng ước lượng cho trung bình:
$\overline{x}\pm t_{\alpha /2}.\frac{s}{\sqrt{n}}$
$1-\alpha$ là độ tin cậy.
Nếu tổng thể có độ lệch cao, hoặc có giá trị bất thường, giá trị khuyến nghị cho cỡ mẫu là 50.
Khi $\sigma$ đã biết:
Cho sai số: $E=z_{\alpha /2}.\frac{\sigma}{\sqrt{n}}$.
Khi đó cỡ mẫu: $n=\frac{(z_{\alpha /2})^2.\sigma^2}{E^2}$.
Khi $\sigma$ chưa biết:
- dùng độ lệch chuẩn các mẫu trước đó, hoặc
- ước tính $\sigma=(max-min)/4$.
Khoảng ước lượng cho tỉ lệ:
$\overline{p}\pm z_{\alpha/2}.\sqrt{\frac{\overline{p}(1-\overline{p})}{n}}$.
Nếu sai số: $E={\alpha/2}.\sqrt{\frac{\overline{p}(1-\overline{p})}{n}}$
thì cỡ mẫu: $n=\frac{(z_{\alpha/2})^2\overline{p}(1-\overline{p})}{E^2}$.
Do chưa chọn mẫu nên ta sẽ chưa có $\overline{p}$.
Ta sẽ sử dụng giá giá trị thay thế là $p^*$.
Giá trị $p^*$ này được chọn bằng cách:
- sử dụng theo các mẫu trước đó
- dự đoán, hoặc
- chọn $p^*=0,5$ (vì khi đó cỡ mẫu sẽ lớn nhất so với các giá trị khác)
Chương 9.
Giả thuyết null: $H_0$ -> cái mới ko giúp cải thiện
Giả thuyết thay thế: $H_a$ phủ định $H_0$
$H_0$: cái mới ko giúp cải thiện
$H_a$: cái mới giúp cải thiện
Nếu kết quả nghiên cứu không đủ mạnh để bác bỏ giả thuyết null, thì điều đó có nghĩa là không có đủ bằng chứng thống kê để kết luận rằng phương pháp mới thực sự tốt hơn. Trong trường hợp đó, có thể cần tiến hành thêm nghiên cứu và kiểm tra để có được kết luận chắc chắn hơn.
Giả thuyết Null như một Giả định bị Thách thức.
Lỗi loại 2: Chấp nhận $H_0$ khi nó sai.
Lỗi loại 1: Bác bỏ $H_0$ khi nó đúng.
Mức ý nghĩa $\alpha$: là xác suất sai lầm loại 1 khi giả thuyết null đúng nhưng chúng ta bác bỏ nó.
Bằng cách không trực tiếp chấp nhận H₀, nhà thống kê tránh được rủi ro mắc sai sót loại II. Bất cứ khi nào xác suất mắc sai sót loại II chưa được xác định và kiểm soát, chúng ta sẽ không đưa ra tuyên bố “chấp nhận H₀.” Trong những trường hợp như vậy, chỉ có hai kết luận có thể: không bác bỏ H₀ hoặc bác bỏ H₀.
Kiểm định 1 phía có 1 trong 2 dạng sau:
Giá trị của kiểm định thống kê: $z=\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}$.
p-value là xác suất cung cấp thước đo bằng chứng chống lại giả thuyết null do mẫu cung cấp.
p-value nhỏ hơn cho thấy có nhiều bằng chứng chống lại $H_0$.
p-value được sử dụng để xác định liệu giả thuyết null có nên bị bác bỏ hay không.
Nếu $\overline{x}<\mu$ thì p-value= diện tích đuôi dưới (bên trái).
Nếu $\overline{x}>\mu$ thì p-value= diện tích đuôi trên (bên phải).
p-value = $P(a\leq z)$ với $a$ là biến có phân phối chuẩn tắc.
Quy tắc dùng p-value: bác bỏ $H_0$ khi p-value $\leq \alpha$.
p-value: mức ý nghĩa quan sát được.
Giá trị tới hạn: là giá trị lớn nhất của thống kê kiểm định sẽ dẫn đến việc bác bỏ giả thuyết null.
Giá trị tới hạn: $-z{\alpha}$
Bác bỏ $H_0$ khi $z\leq z_{\alpha}$.
Kiểm định 2 phía:
$H_0: \mu =\mu_0$
$H_a: \mu\neq\mu_0$
Tính p-value:
- tính $z=\frac{\overline{x}-\mu_0}{\sigma/\sqrt{n}}$.
- tìm diện tích đuôi 1 bên.
- nhân 2 để được p-value.
Tính giá trị tới hạn:
- tính $\alpha/2$
- tra bảng để tìm ra giá trị $z_{\alpha}$ và $-z_{\alpha}$
Một số hướng dẫn mà các nhà thống kê gợi ý để giải thích các giá trị p nhỏ.
- Nhỏ hơn 0,01 – Bằng chứng áp đảo để kết luận Ha là đúng.
- Giữa 0,01 và 0,05 – Bằng chứng mạnh để kết luận Ha là đúng.
- Giữa 0,05 và 0,10 – Bằng chứng yếu để kết luận Ha là đúng.
- Lớn hơn 0,10 – Không đủ bằng chứng để kết luận Ha là đúng.
Excel:
- tìm z: norm.inv
- tìm p: norm.dist
$t=\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$
Excel: (dành cho t>0, nếu t<0 thì lấy đối xứng)
- tìm t: t.inv
- tìm p: t.dist.rt
Kích thước mẫu:
- 30: tốt
- 15: nếu tổng thể gần chuẩn
- 50: tổng thể lệch nhiều, hoặc có chứa ngoại lệ