Toán 12 | Cơ bản
Chương 1.
Đồng biến: cho tùy ý $a>b$ thì $f(a)>f(b)$.
Nghịch biến: cho tùy ý $c>d$ thì $ g(c) < g(d) $.
Đồng biến hoặc nghịch biến gọi chung là đơn điệu.
Đồng biến khi $f'(x) > 0$ và ngược lại.
Nghịch biến khi $g'(x) < 0$ và ngược lại.
4 bước xác định tính đơn điệu:
- tìm tập xác định -> chỉ ra các giá trị ko xác định
- tính $f'(x)$
- tìm nghiệm của phương trình $f'(x)=0$
- lập bảng biến thiên rồi đưa ra kết luận
Định lí Lagrange: có số $c$ ở giữa $a,b$ sao cho $\displaystyle f'(c)= \frac{ f(a) – f(b) }{ a-b } $.
Bài tập:
Test1 | Đồng biến, nghịch biến
Điểm cực đại: các điểm ở đỉnh
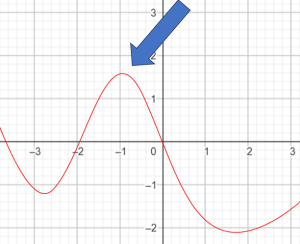
Giá trị cực đại là giá trị của $f(x)$ tại điểm cực đại (tức là tọa độ $y$).
Điểm cực tiểu: các điểm ở đáy
Giá trị cực tiểu là giá trị của $f(x)$ tại điểm cực tiểu.
Các điểm cực đại hay cực tiểu gọi chung là điểm cực trị.
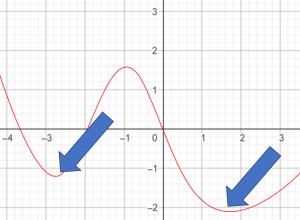
Chú ý là các điểm cực trị ta sẽ ko lấy ở biên bên trái hoặc bên phải.
Tại các điểm cực trị ta có $f'(x)=0$.
Ngược lại, khi $f'(x)=0$ thì chưa chắc đó là vị trí cực trị.
Ở đó chỉ trở thành cực trị khi 2 bên trái phải của x, hàm số có giá trị 1 bên âm, 1 bên dương.
Khi $f'(x)=0$ ở vị trí cực trị.
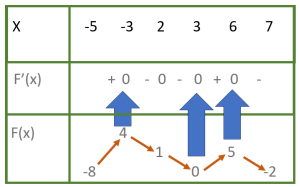
Để ý 2 bên số 0 ở vị trí cực trị sẽ là các dấu + và -.
Khi $f'(x)=0$ ở vị trí ko phải cực trị.
Để ý 2 bên số 0 đều là dấu -.
Nếu 2 bên số 0 đều là dấu + thì cũng ko có cực trị.
Chú ý ở đây ta đều xét ở dòng $f'(x)$.
Cực tiểu: $f'(x)=0$ và $f”(x)>0$.
Cực đại: $f'(x)=0$ và $f”(x)<0$.
4 bước tìm cực trị:
- tìm tập xác định -> chỉ ra các giá trị ko xác định
- tính $f'(x)$.
- tìm nghiệm của phương trình $f'(x)=0$. Giả sử các nghiệm tìm được là $a,b,c,…$
- chọn 1 trong 2 cách làm sau:
- lập bảng biến thiên rồi dựa vào đó kết luận.
- tính $f”(x)$ rồi tính $f”(a), f”(b), f”(c),…$ rồi dựa vào đó kết luận.
Khi $f'(x)=0$ và $f”(x)=0$ thì ở đó ko phải là cực trị.
Bài tập:
Test2 | Cực trị
Khi nhắc đến giá trị của hàm số tức là ta đang nói đến giá trị $f(x)$ tương ứng với giá trị y trên đồ thị.
Quan sát đồ thị sau:
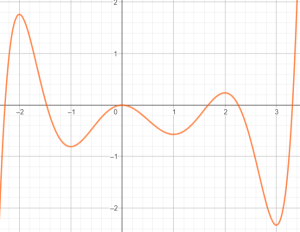
Ta thấy trên đường màu cam, vị trí cao nhất có độ cao bằng 2, vị trí thấp nhất có độ cao bằng -2,3.
Khi đó, ta nói hàm số có giá trị lớn nhất là 2 và giá trị nhỏ nhất là -2,3.
Để ý là các giá trị 2 và -2,3 là lấy trên trục dọc.
Tuy nhiên, khoảng giá trị của $x$ ta chỉ lấy từ khoảng -2,4 đến 3,4 (các số trên trục ngang) nên ta sẽ kí hiệu:
$\underset{[-2,4 ; 3,4]}{\max} f(x)=2$.
$\underset{[-2,4 ; 3,4]}{\min} f(x)=-2,3$.
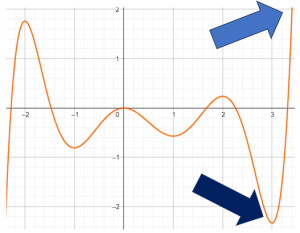
Bây giờ, cũng với đồ thị trên, thử tìm $\underset{[-1 ; 2]}{\max} f(x)$ và $\underset{[-1 ; 2]}{\min} f(x)$.
Lúc này, ta chỉ cần quan sát đoạn đồ thị khi $x$ nằm trong khoảng $[-1;2]$ và chú ý các vị trí có độ cao lớn nhất, nhỏ nhất.
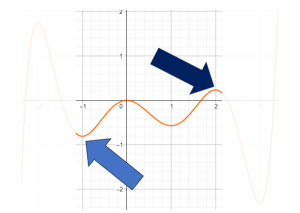
Rõ ràng: $\underset{[-1 ; 2]}{\max} f(x)=0,2$ và $\underset{[-1 ; 2]}{\min} f(x)=-0,8$ (chú ý là lấy các giá trị trên trục dọc).
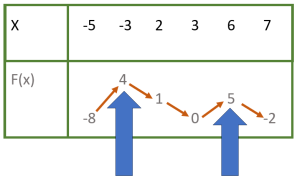
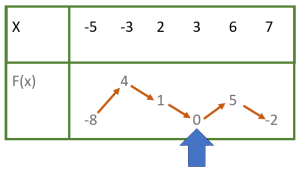
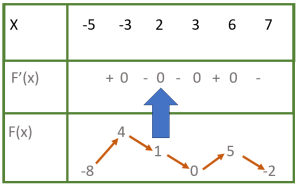
Thử tìm max, min của hàm số dựa vào bảng biến thiên sau: 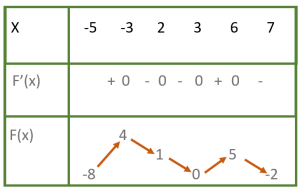
Khi $x$ đi từ -5 đến 3 thì $F(x)$ đi từ -8 lên 4 rồi giảm xuống 1, sau đó giảm xuống 0.
Nên $\underset{[-5 ; 3]}{\max} f(x)=4$ và $\underset{[-5 ; 3]}{\min} f(x)=-8$.
Nếu xét trên toàn bảng thì ta cũng có $\underset{[-5 ; 7]}{\max} f(x)=5$ và $\underset{[-5 ; 7]}{\min} f(x)=-8$.
3 bước tìm max, min:
- tính $f'(x)$.
- tìm nghiệm của phương trình $f'(x)=0$ và các giá trị làm cho $f'(x)$ ko xác định. Giả sử các giá trị $x$ tìm được nằm trong khoảng tìm max, min là $a,b,c,d…$.
- tính $f(a),f(b),f(c),f(d),…$.
- số lớn nhất và nhỏ nhất trong các giá trị ở bước trên là các giá trị cần tìm.
Bài tập:
Test3 | max, min
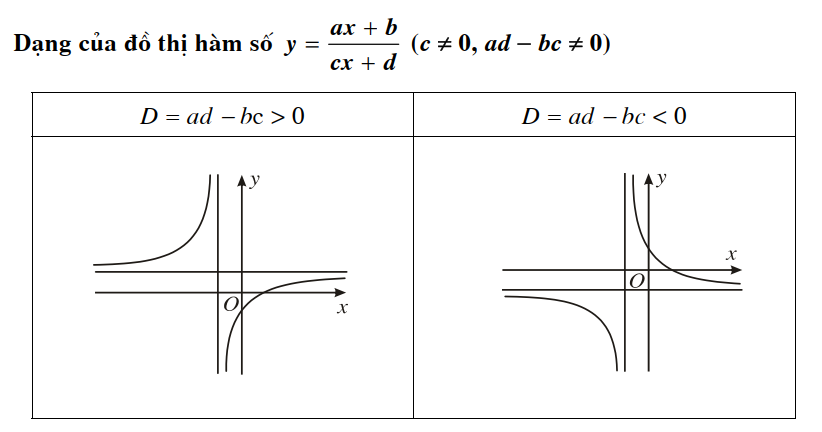
Đường tiệm cận ngang:
- là đường nằm ngang
- sẽ tiến gần sát với đồ thị khi:
- $x$ tăng rất lớn ($x \rightarrow +\infty $) hoặc
- $x$ giảm rất nhỏ ($x \rightarrow -\infty $)
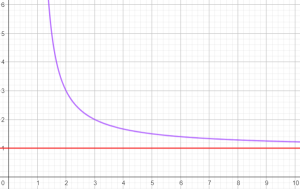
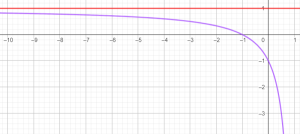
Đường thẳng $y=a$ là tiệm cận ngang nếu có: $\underset{x\rightarrow +\infty}{\lim}f(x)=a$ hoặc $\underset{x\rightarrow -\infty}{\lim}f(x)=a$.
Đường tiệm cận đứng:
- là đường nằm thẳng đứng
- sẽ tiến gần sát với đồ thị khi:
- $y$ tăng rất lớn ($y \rightarrow +\infty $) hoặc
- $y$ giảm rất nhỏ ($y \rightarrow -\infty $)
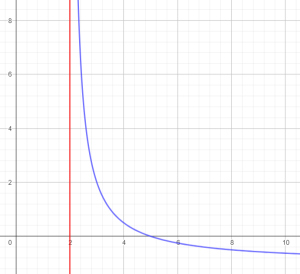
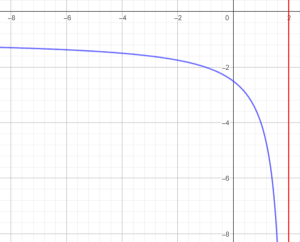
Đường thẳng $x=b$ là tiệm cận đứng nếu có:
- $\underset{x\rightarrow b^+}{\lim}f(x)=+\infty$ hoặc
- $\underset{x\rightarrow b^-}{\lim}f(x)=+\infty$ hoặc
- $\underset{x\rightarrow b^+}{\lim}f(x)=-\infty$ hoặc
- $\underset{x\rightarrow b^-}{\lim}f(x)=-\infty$.
Bài tập:
Test4 | Tiệm cận
Khảo sát hàm số: tìm hiểu sự thay đổi giá trị của hàm số.
3 bước khảo sát hàm số:
- tìm tập xác định -> chỉ ra các giá trị $x$ làm cho $f(x)$ ko xác định
- lập bảng biến thiên:
- tính $f'(x)$
- tìm các giá trị $x$ để $f'(x)=0$ hoặc $f'(x)$ ko xác định
- xét sự âm, dương của $f'(x)$ rồi suy ra sự đồng biến, nghịch biến của $f(x)$
- tìm cực trị
- tìm các giới hạn của $f(x)$ khi $x$ tiến tới vô cùng
- tìm các tiệm cận
- vẽ đồ thị: dựa vào bảng biến thiên
Nếu hàm số tuần hoàn thì chỉ cần khảo sát trên 1 chu kì.
Để thuận lợi trong lúc vẽ đồ thị thì nên chú ý thêm:
- giao điểm của đồ thị với các trục tọa độ
- tính chẵn, lẻ và đối xứng
Các hàm số thường được khảo sát trong chương trình toán 12 là:
- hàm bậc 3
- hàm bậc 4
- hàm phân thức
Đối với hàm phân thức:
- tính $\lim f(x)$ khi $x$ tiến gần đến các giá trị mà $f(x)$ ko xác định, từ đó xác định tiệm cận ngang
- tính $\lim f(x)$ khi $x$ tiến ra vô cùng để xác định tiệm cận đứng
Đồ thị của 2 hàm số $f(x)$ và $g(x)$ sẽ cắt nhau ở vị trí làm cho $f(x)=g(x)$.
Điểm A tọa độ $(m,n)$ sẽ nằm trên đồ thị của $f(x)$ nếu $f(m)=n$.
Điểm A tọa độ $(m,n)$ sẽ nằm trên đồ thị của $g(x)$ nếu $g(m)=n$.
Vậy nên điểm A vừa ở trên đồ thị của $f(x)$, vừa ở trên đồ thị của $g(x)$ thì phải có $f(m)=g(m)$.
Số giao điểm của 2 đồ thị của $f(x)$ và $g(x)$ sẽ bằng số nghiệm của phương trình $f(x)=g(x)$.
Bài tập:
Test5 | Hàm bậc 3
Test6 | Hàm bậc 3 ko cực trị mà f’=0
Test7 | Hàm bậc 3 ko cực trị
Test8 | Hàm phân thức
Test9 | Giao điểm 2 đồ thị
Chương 2.
$a^n = \underset{n \text{ số }a}{\underbrace{a.a…a}}$
$a$ là cơ số, $n$ là số mũ.
$a^0=1$
$a^{-n}=\frac{1}{a^n}$
$0^0, 0^{-n}$ ko xác định.
Phương trình bậc lẻ (số mũ $n$ lẻ): $x^n=b$ có 1 nghiệm là $x=\sqrt[n]{b}$.
Phương trình bậc chẵn (số mũ $m$ chẵn): $x^m=d$
- nếu $d<0$ thì vô nghiệm
- nếu $d=0$ thì có 1 nghiệm $x=0$
- nếu $d>0$ thì có 2 nghiệm $x=\sqrt[m]{d}$ và $x=-\sqrt[m]{d}$
$\sqrt[n]{a}.\sqrt[n]{b}=\sqrt[n]{ab}$
$\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
$\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
$\sqrt[n]{a^n}=\begin{cases}
a& \text{nếu }n\text{ lẻ }\\
|a|& \text{nếu }n\text{ chẵn }
\end{cases}$
$\displaystyle a^{\frac{m}{n}}=\sqrt[n]{a^m}$
Cho $a,b$ dương. Ta có:
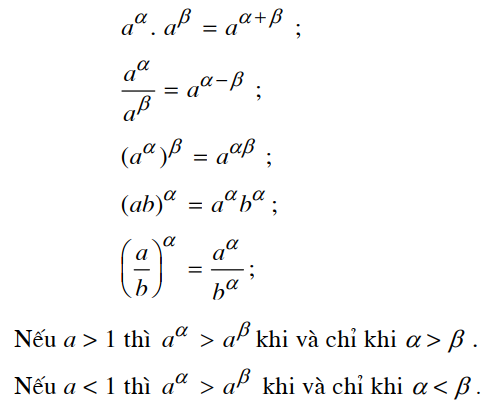
Bài tập:
Test10 | Lũy thừa
$f(x)=x^a$
$f'(x)=a. x^{a-1}$
$\left ( g(x)^a \right )’=a. g(x)^{a-1}.g'(x)$
Khi $a=1$ thì $f(x)=x$
$(x)’=1$
Khi $a=0$ thì $f(x)=x^0=1$
$(1)’=0$
Đồ thị 1 số hàm lũy thừa:
$x$: 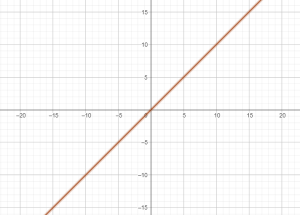
$x^4$: 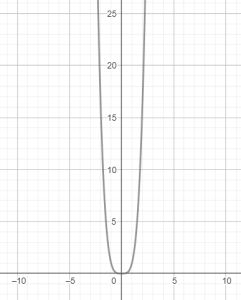
$x^7$: 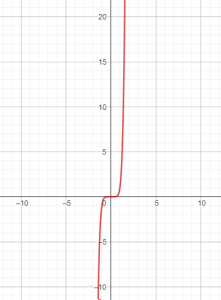
$x^{-4}$: 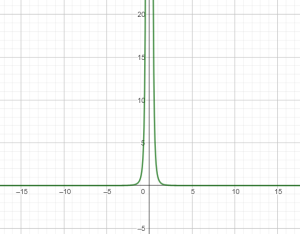
$x^{-5}$: 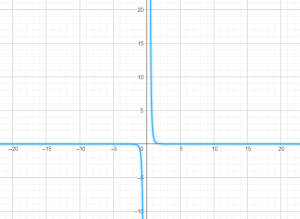
Để ý: khi $a<0$ thì đồ thị của $f(x)=x^a$ có 1 đường tiệm cận đứng và 1 đường tiệm cận ngang.
Bài tập:
Test11 | Hàm lũy thừa
Nếu $a^x=b$ thì $x=\log_a b$.
Có thể nói hàm loagarit (log) là hàm để tìm số mũ.
$\log_a a^y=y$
Vì $a^0=1$ nên $\log_a 1=0$
Vì $a^1=a$ nên $\log_a a=1$
Nếu $\log_a b=x$ thì $a^x=b$. Suy ra $a^{\log_a b}=a^x=b$
Một số công thức của hàm log:
$\log_a (b.c)=\log_a b + \log_a c$
$\log_a \frac{b}{c}=\log_a b – \log_a c$
$\log_a \frac{1}{x}=\log_a 1 – \log_a x = 0 – \log_a x = -\log_a x$
$\log_a b^x=x.\log_a b$ nếu $b>0$
$\log_a b^x=x.\log_a |b|$ nếu $b<0$
$\log_a \sqrt[n]{x}=\log_a \left ( x^{\frac{1}{n}} \right )=\frac{1}{n}.\log_a x$
$\log_{(a^n)}x=\frac{1}{n}\log_a x$
$\log_a b = \frac{\log_c b}{\log_c a}$ với số $c$ dương và khác 1 tùy ý.
$\log_a b = \frac{\log_b b}{\log_b a}=\frac{1}{\log_b a}$
Logarit thập phân: $\log_{10} x = \log x = \lg x$
Logarit tự nhiên: $\log_e x=\ln x$
với $e\approx 2,718$
Để ý:
- khi $a>1$:
- nếu $b>a$ thì $\log_a b=x>0$
- nếu $b<a$ thì $\log_a b=x<0$
- khi $1>a>0$:
- nếu $b>a$ thì $\log_a b=x<0$
- nếu $b<a$ thì $\log_a b=x>0$
Bài tập:
Test12 | Logarit
$f(x)=a^x$ với $a$ dương, khác 1.
$\left ( a^x \right )’=a^x.\ln a$
$\left ( e^x \right )’=a^x.\ln e=a^x.1=a^x$
$\left ( a^{g(x)} \right )’=a^{g(x)}.\ln a.g'(x)$
Đồ thị 1 số hàm mũ:
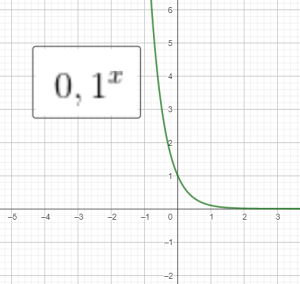
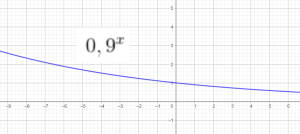
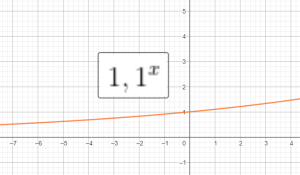
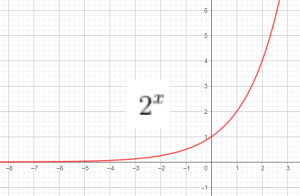
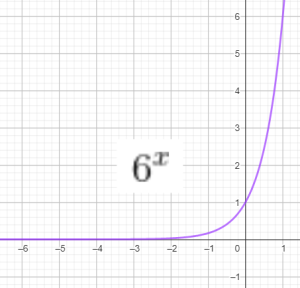
Bài tập:
Test13 | Hàm mũ
$f(x)=\log_a x$
$\left ( \log_a x \right )’=\frac{1}{x.\ln a}$
$\left ( \ln x \right )’=\left ( \log_e x \right )’=\frac{1}{x.\ln e}=\frac{1}{x.\log_e e}=\frac{1}{x.1}=\frac{1}{x}$
$\left ( \log_a g(x) \right )’=\frac{1}{x.\ln a}.g'(x)=\frac{g'(x)}{x.\ln a}$
Đồ thị của 1 số hàm log:
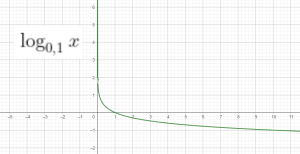
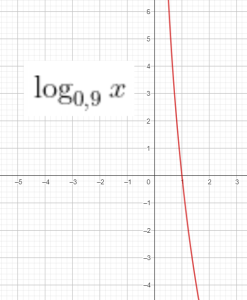
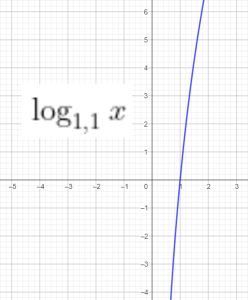
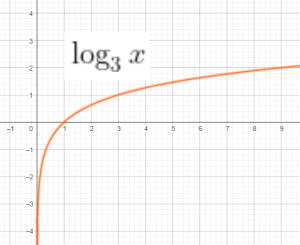
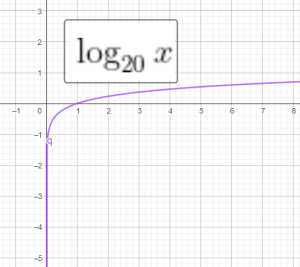
Bài tập:
Test14 | Hàm logarit
Phương trình $a^x=b$ với $a$ dương khác 1:
- nếu $b>0$ thì $x=\log_a b$
- nếu $b\leq 0$ thì vô nghiệm
Bài tập:
Test15 | Phương trình mũ
Xét $a$ dương, khác 1
Dạng 1:
$a^x>b$
$a^x<b$
$a^x\geq b$
$a^x\leq b$
Vì $a^x$ luôn dương nên
- khi $b\leq 0$:
- $a^x<b$ vô nghiệm
- $a^x\leq b$ vô nghiệm
- $a^x>b$ có nghiệm $x\in R$ tùy ý
- $a^x\geq b$ có nghiệm $x\in R$ tùy ý
- khi $b>0$:
- **nếu $a>1$:
- $a^x<b$ có nghiệm $x<\log_a b$
- $a^x\leq b$ có nghiệm $x\leq\log_a b$
- $a^x>b$ có nghiệm $x>\log_a b$
- $a^x\geq b$ có nghiệm $x\geq\log_a b$
- **nếu $1>a>0$: dấu $>,<$ sẽ đảo chiều
- $a^x<b$ có nghiệm $x>\log_a b$
- $a^x\leq b$ có nghiệm $x\geq\log_a b$
- $a^x>b$ có nghiệm $x<\log_a b$
- $a^x\geq b$ có nghiệm $x\leq\log_a b$
- **nếu $a>1$:
Dạng 2:
$a^x>a^b$
- nếu $a>1$ thì $x>b$
- nếu $1>a>0$ thì $x<b$
Bài tập:
Test17 | Bất phương trình mũ
$\log_a x>b$
- **nếu $a>1$: nghiệm là
- $x>a^b$
- **nếu $1>a>0$: dấu $>$ sẽ đảo chiều
- $0<x<a^b$
Bài tập:
Test18 | Bất phương trình logarit
Chương 3.
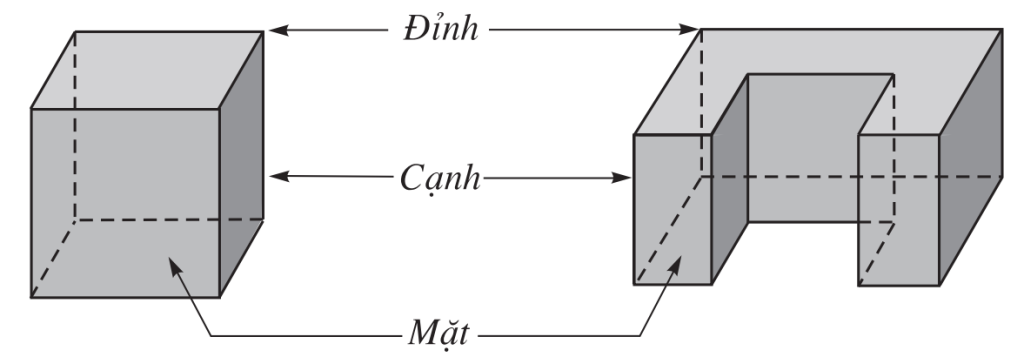
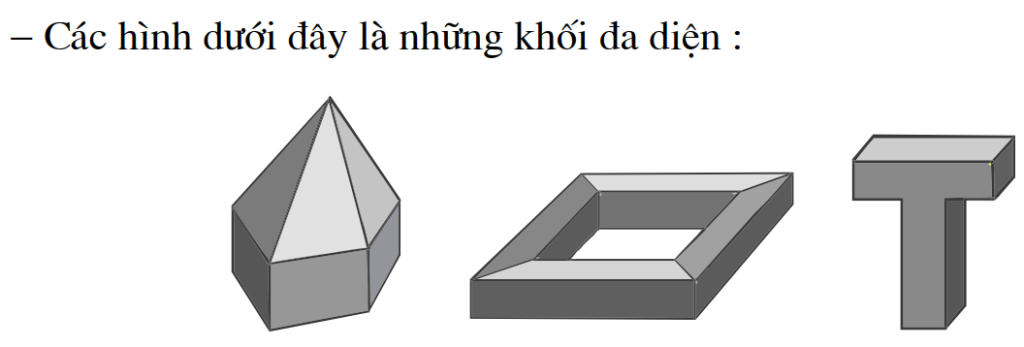
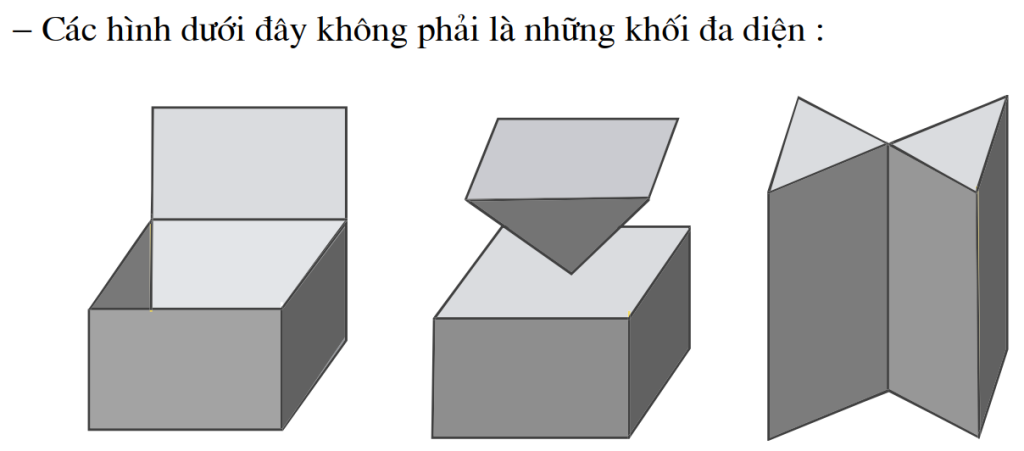
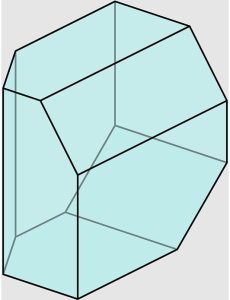
Đa diện lồi:

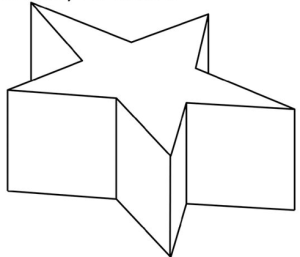
Đa diện không lồi:
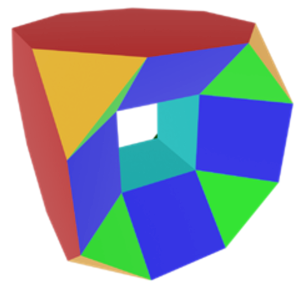
Đa diện đều:
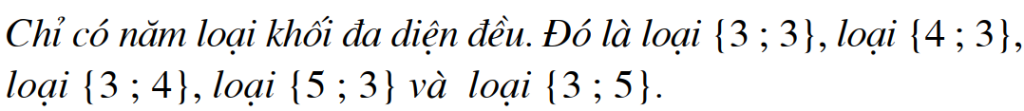
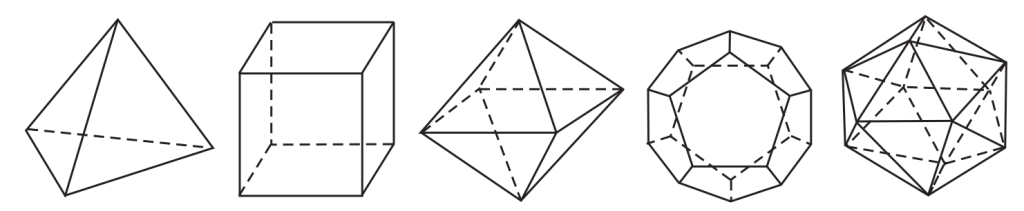
3 loại các mặt là tam giác:
- {3 ; 3} -> 4 mặt
- {3 ; 4} -> 8 mặt
- {3 ; 5} -> 12 mặt
1 loại các mặt là tứ giác: {4 ; 3} -> 6 mặt
1 loại các mặt là ngũ giác: {5 ; 3} -> 20 mặt
Công thức Euler: (số đỉnh) – (số cạnh) + (số mặt) = 2
Bài tập:
Test26 | Tổng quan về khối đa diện
Hình chóp tứ giác:
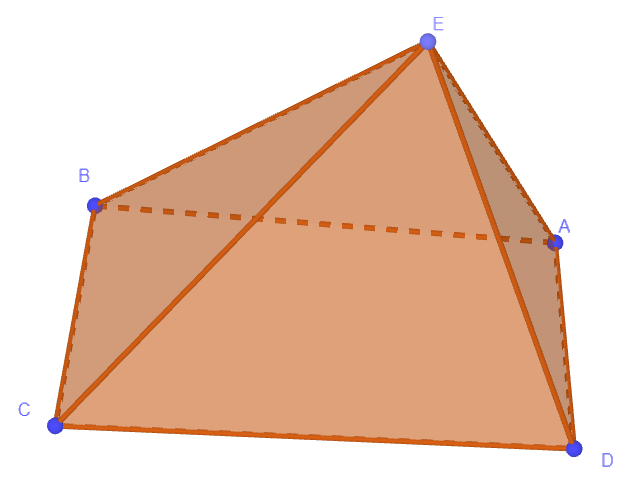
Đỉnh: E
Đáy: tứ giác ABCD
Các cạnh đáy: AB, BC, CD, DA
Các cạnh bên: EA, EB, EC, ED
Các mặt bên: (EAB), (EBC), (ECD), (EDA).
Hình chóp tam giác:
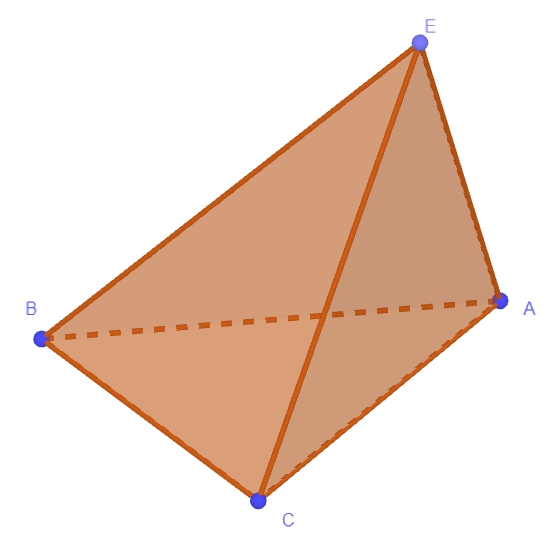
Thể tích = $\frac{1}{3}$(Diện tích đáy) x (Chiều cao)
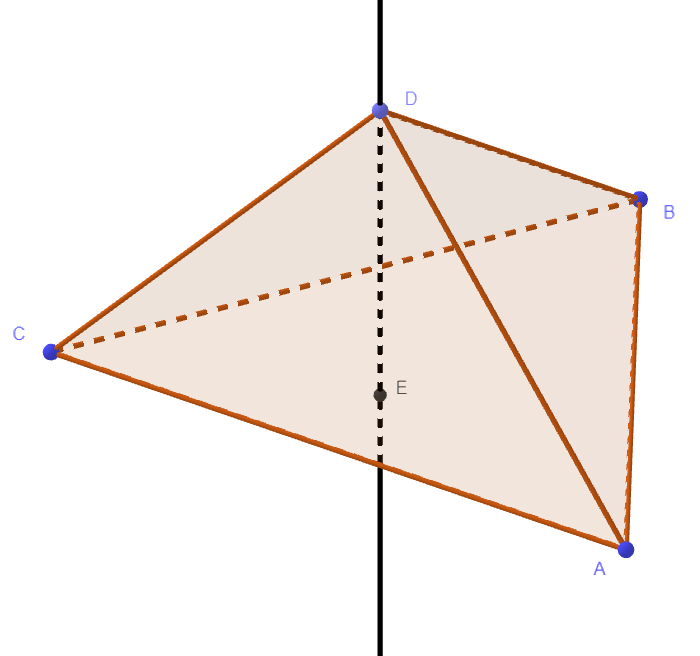
Đường màu đen đi qua đỉnh D và vuông góc với mặt đáy.
Điểm E nằm trên đường đó và cũng nằm trên mặt đáy.
Đoạn DE chính là chiều cao của hình chóp.
Thể tích của hình chóp trên =$\frac{1}{3}$(Diện tích đáy ABC) x (Chiều cao DE).
Bài tập:
Test27 | Khối chóp
- 2 đáy song song và bằng nhau.
- Các cạnh bên song song và bằng nhau.
- Các mặt bên là hình bình hành.
Hình lăng trụ tứ giác:
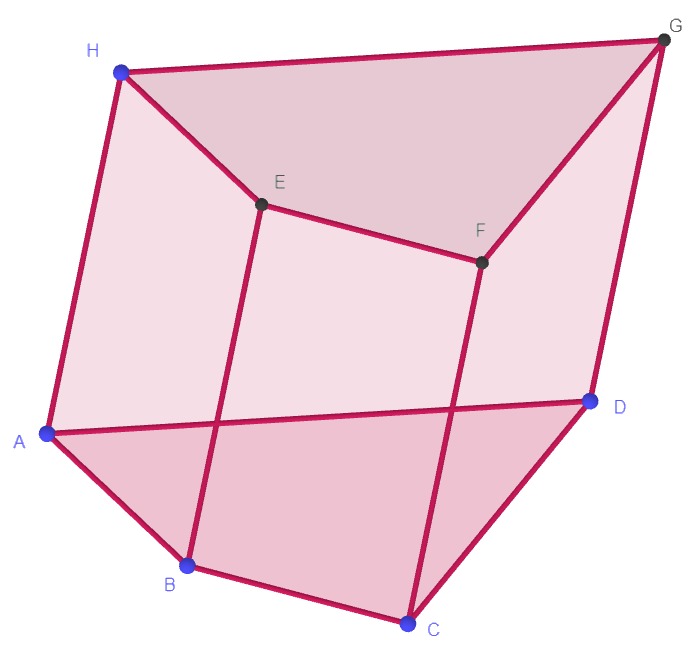
Hình lăng trụ tam giác:
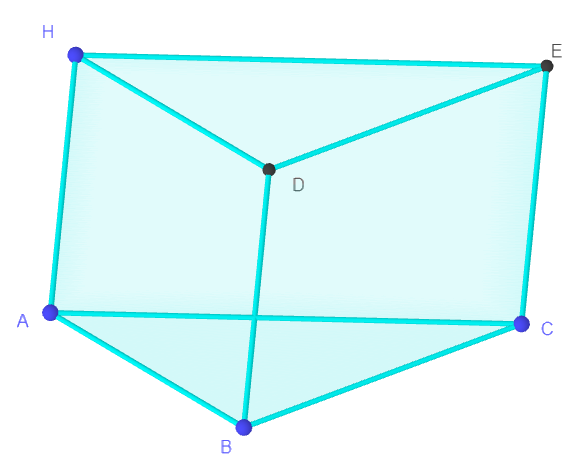
Hình lăng trụ đứng:
Các cạnh bên vuông góc với 2 đáy.
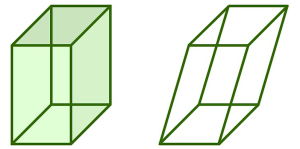
Hình bên trái là lăng trụ đứng.
Hình lăng trụ đều:
Là lăng trụ đứng có đáy là đa giác đều.
Thể tích = (Diện tích 1 đáy) x (Chiều cao)
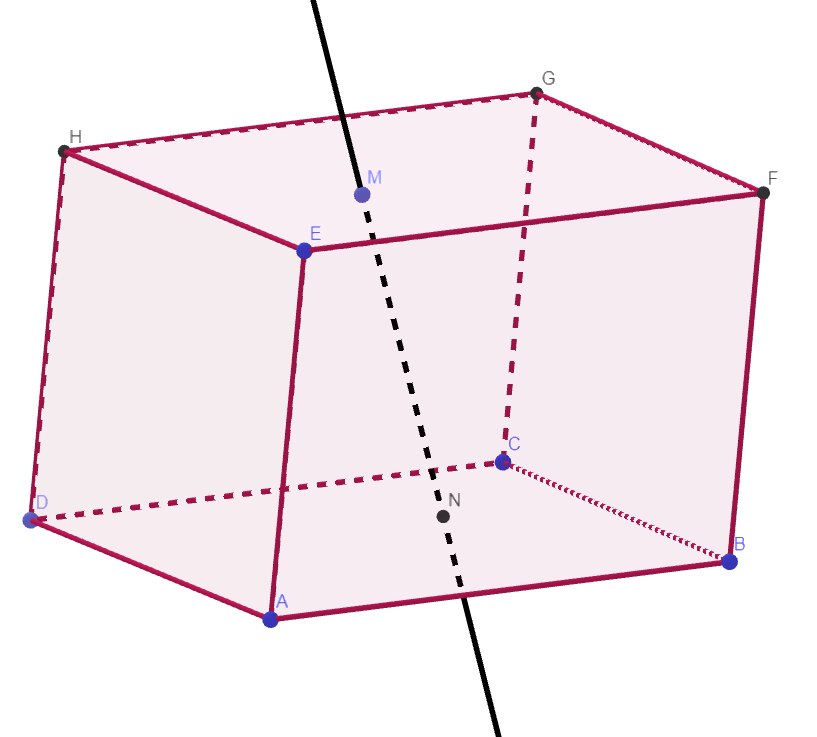
Đường màu đen vuông góc với 2 đáy.
Các điểm M, N nằm trên đường màu đen và cũng nằm trên các đáy.
Chiều cao của lăng trụ trên chính là độ dài đoạn MN.
Bài tập:
Test28 | Khối lăng trụ
Chương 4.
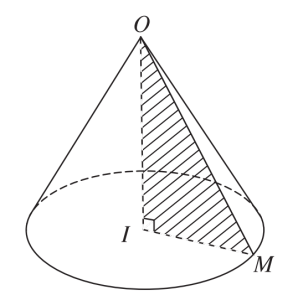
OI vuông góc với mặt phẳng chứa hình tròn tâm I.
Di chuyển điểm M quanh đường tròn tâm I. Lúc đó, dấu vết tạo ra bởi đoạn OM chính là mặt nón.
Còn dấu vết tạo bởi tam giác OIM khi M di chuyển tạo ra khối nón.
Mặt cong tạo bởi việc xoay đoạn OM được gọi là mặt xung quanh của hình nón.
Đáy của hình nón là hình tròn.
Bán kính đáy là IM (R).
OM được gọi là đường sinh $(l)$.
OI là chiều cao của hình nón $(h)$.
O là đỉnh của hình nón.
OI là trục của hình nón.
Diện tích xung quanh của hình nón (diện tích mặt nón): $S_{xq}=\pi.R.l$
Thể tích hình nón: $V=\frac{1}{3}S_{\text{đáy}}.h=\frac{1}{3}.\pi.R^2.h$
Mối quan hệ của các kích thước trong hình nón: $l^2=R^2+h^2$
Bài tập:
Test29 | Mặt nón
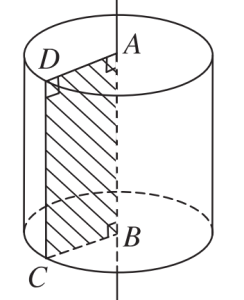
Khi xoay hình chữ nhật ABCD xung quanh trục AB, vết của đoạn CD tạo ra mặt trụ, còn vết của hình chữ nhật ABCD tạo ra khối trụ.
Mặt trụ tạo bởi CD cũng được gọi là mặt xung quanh của hình trụ.
Hình trụ có 2 đáy là 2 hình tròn song song và bằng nhau với các tâm là A, B, bán kính bằng BC ($R$).
CD là đường sinh, cũng là chiều cao ($h$).
AB vuông góc với 2 mặt đáy.
AB là trục của hình trụ.
Diện tích mặt xung quanh của hình trụ: S= (Chu vi đáy) x (Chiều cao) = $2\pi.R.h$.
Thể tích khối trụ: V= (Diện tích đáy) x (Chiều cao) = $\pi.R^2.h$
Bài tập:
Test30 | Mặt trụ
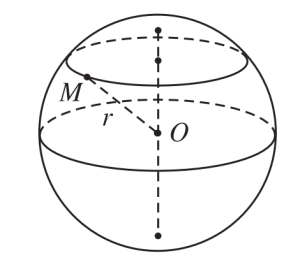
Dây cung: đoạn thẳng nối 2 điểm trên mặt cầu.
Bán kính ($R$): bằng khoảng cách từ tâm O đến điểm M bất kỳ trên mặt cầu.
Đường kính: là dây cung đi qua tâm.
Đường kính = 2 lần bán kính.

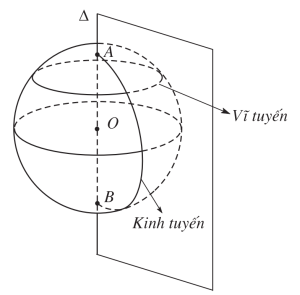
Kinh tuyến: là các nửa đường tròn bằng nhau
Vĩ tuyến: là các đường tròn.
Bài tập:
Test31 | Mặt cầu
Mặt cầu và mặt phẳng ko có điểm chung: $OH>R$
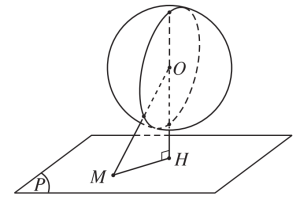
Mặt cầu và mặt phẳng tiếp xúc nhau (chỉ có 1 điểm chung): $OH=R$
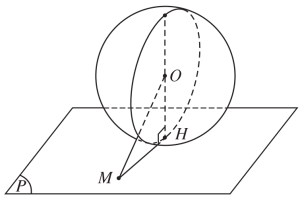
Mặt cầu và mặt phẳng cắt nhau: $OH<R$, phần chung là 1 đường tròn
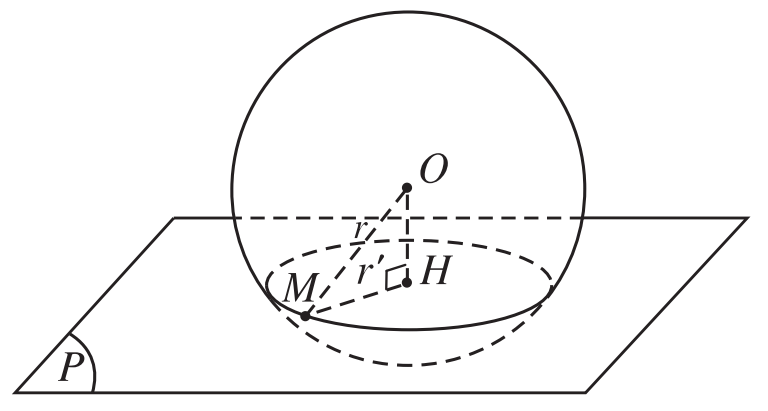
Mặt phẳng đi qua tâm của mặt cầu:
Mặt phẳng này được gọi là mặt phẳng kính của hình cầu.
Bài tập:
Test32 | Mặt cầu giao mặt phẳng
Đường thẳng và hình cầu ko có điểm chung:
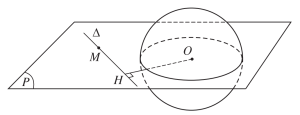
Đường thẳng và hình cầu tiếp xúc nhau (chỉ có 1 điểm chung): -> đường tiếp tuyến
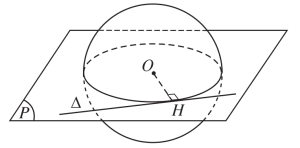
Đường thẳng và hình cầu cắt nhau: có 2 điểm chung
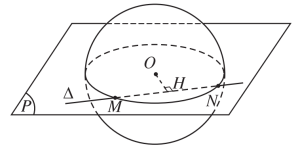
Qua điểm A trên mặt cầu, có vô số đường tiếp tuyến.
Các đường này cùng nằm trên 1 mặt phẳng.
Các đường tiếp tuyến này đều vuông góc với OA.
Mặt phẳng này gọi là mặt tiếp tuyến của hình cầu.
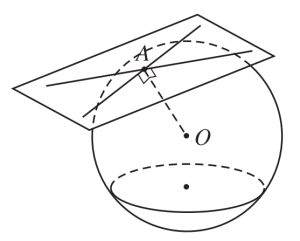
Từ điểm A ngoài mặt cầu, có vô số tiếp tuyến của mặt cầu và đi qua A.
Các tiếp tuyến này tạo ra 1 mặt nón.
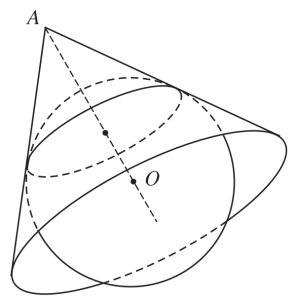
Mặt nón ngoại tiếp mặt cầu khi: mặt xung quanh của nón và đáy nón tiếp xúc với mặt cầu.
Bài tập:
Test33 | Mặt cầu giao đường thẳng, tiếp tuyến
Diện tích mặt cầu: $S=4\pi.R^2$
Thể tích khối cầu: $V=\frac{4}{3}.\pi.R^3$
Bài tập:
Test34 | Diện tích, thể tích mặt cầu
Chương 5.
Nếu $\left ( N \right )’=D$ thì ta nói:
- $D$ là đạo hàm của $N$, và
- $N$ là 1 nguyên hàm của $D$
Để ý: $N+1, N+2, N+3,…$ cũng là các nguyên hàm của $D$ vì chúng đều có đạo hàm bằng $D$.
Có thể nói công thức chung của nguyên hàm của $D$ là: $D+c$ với $c$ là 1 con số tùy ý.
Kí hiệu tất cả các nguyên hàm của D là: $\int D dx=N+c$
Quy ước: $\int dx=\int 1dx$
Tính chất:
$\int f'(x) dx=f(x)+c$
$\int a.f(x) dx=a.\int f(x) dx$ với $a$ là con số khác 0.
$\int (A+B) dx=\int A dx+\int B dx$
$\int (A-B) dx=\int A dx-\int B dx$

- khi $x>0$: $\int \frac{1}{x}dx=\ln x+c$
- khi $x<0$: $\int \frac{1}{x}dx=\ln (-x)+c$
Phương pháp đổi biến:
- đặt $u=g(x)$
- tính $du=g'(x).dx$
- suy ra $dx=\frac{1}{g'(x)}du$
- tính $\int …du$ theo $u$
- thay $u=g(x)$
Phương pháp nguyên hàm từng phần:
- nhìn ra kiểu: $\int f(x)dx=\int \left ( A.B \right )dx$
- xác định $u=A$, và $v$ sao cho $(v)’=B$
- tính $u’$
- thay vào công thức: $\int f(x)dx=\int \left ( u.v’ \right )dx=u.v-\int \left ( u’.v \right )dx$
Bài tập:
Test19 | Nguyên hàm
Giả sử ta có $\int D dx=N+c$.
Tích phân của $D$ từ $a$ đến $b$ là: $\int_{a}^{b}Ddx=N|_a^b=N(b)-N(a)$.
$a$ là cận dưới, $b$ là cận trên.
Từ đó, ta có:
$\int_{a}^{b}Ddx=-\int_{b}^{a}Ddx$
$\int_{a}^{a}Ddx=0$
Tính chất:
$\int_{a}^{b} k.f(x) dx=k.\int_{a}^{b} f(x) dx$ với $k$ là con số
$\int_{a}^{b} (A+B) dx=\int_{a}^{b} A dx+\int_{a}^{b} B dx$
$\int_{a}^{b} (A-B) dx=\int_{a}^{b} A dx-\int_{a}^{b} B dx$
$\int_{a}^{b}Ddx+\int_{b}^{c}Ddx=\int_{a}^{c}Ddx$
Phương pháp đổi biến:
- đặt $u=g(x)$
- tính $du=g'(x).dx$
- suy ra $dx=\frac{1}{g'(x)}du$
- đổi cận: tìm $m,n$ sao cho $m=g(a), n=g(b)$
- dùng tính chất: $\int_{a}^{b}…dx=\int_{m}^{n}…du$
- tính tích phân theo biến mới là $u$
Phương pháp tích phân từng phần:
- nhìn ra kiểu: $\int f(x)dx=\int \left ( A.B \right )dx$
- xác định $u=A$, và $v$ sao cho $(v)’=B$
- tính $u’$
- thay vào công thức: $\int f(x)dx=u.v|_{a}^{b}-\int_{a}^{b} \left ( u’.v \right )dx$
Bài tập:
Test20 | Tích phân
Tính diện tích:
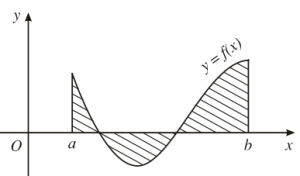
Diện tích phần gạch chéo: $S=\int_{a}^{b}|f(x)-0|dx=\int_{a}^{c}f(x)dx-\int_{c}^{d}f(x)dx+\int_{d}^{b}f(x)dx$ với $(c;d)$ là đoạn mà $f(x)$ âm.
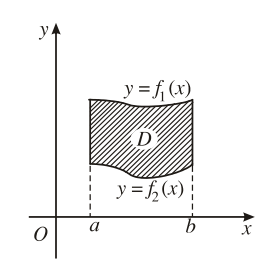
$S=\int_{a}^{b}|f_1(x)-f_2(x)|dx$
Tính thể tích:
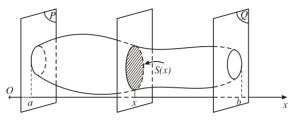
$V=\int_{a}^{b}S(x)dx$
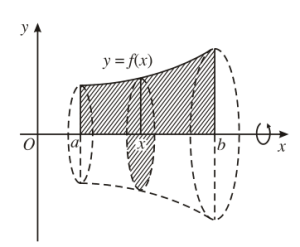
$V=\pi\int_{a}^{b}f^2(x)dx$
Bài tập:
Test21 | Tích phân trong hình học
Chương 6.
Số $i$ là số có tính chất: $i^2=-1$
Số phức là số kiểu: $a+b.i$
Số phức có 2 phần:
- phần thực: $a$
- phần ảo: $b$
Tập hợp các số phức: $\mathbb{C}$
Số phức bằng nhau: $a+bi=c+di$ khi $a=c$ và $b=d$ $(a,b,c,d\in R)$
Số thực là 1 kiểu số phức: $a=a+0.i$
Số thuần ảo: phần thực bằng 0 -> $0+b.i$
Số $i$ được gọi là đơn vị ảo -> $i=0+1.i$
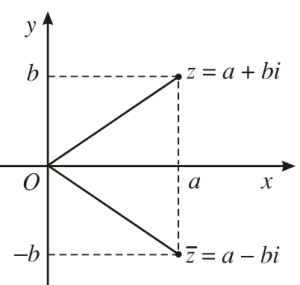
Biểu diễn số phức trên mặt phẳng tọa độ:
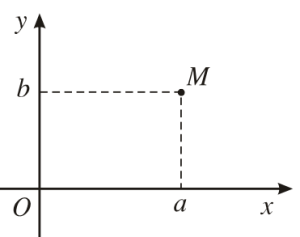
Điểm M biểu diễn số phức: $a+bi$
Modun của số phức: $|a+bi|=\sqrt{a^2+b^2}$, bằng độ dài đoạn OM, bằng độ dài vector: $\left | \overrightarrow{OM} \right |$.
Số phức liên hợp: $\overline{a+bi}=a-bi$ (chỉ thay đổi dấu của phần ảo).
Bài tập:
Test22 | Số phức là gì
$a+bi+c+di=a+c+(b+d)i$
$a+bi-(c+di)=a-b+(c-d)i$
$(a+bi).(c+di)=ac+adi+bic+bidi$
$=ac+adi+bci+bdi^2$
$=ac+(ad+bc)i+bd.(-1)$ (vì $i^2=-1$)
$=ac-bd + (ad+bc)i$
Bài tập:
Test23 | Cộng, trừ, nhân số phức
Cho $z=a+bi$. Ta có:
$z+\overline{z}=a+bi+a-bi=2a$
$z.\overline{z}=(a+bi).(a-bi)=a^2-(bi)^2=a^2-b^2.i^2=a^2+b^2$ (vì $i^2=-1$)
$=\left ( \sqrt{a^2+b^2} \right )^2=|z|^2$
Cách chia số phức:
$\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}$
$=\frac{ac+bd+(ad-bc)i}{c^2+d^2}$
$=\frac{ac+bd}{c^2+d^2}+\frac{(ad-bc)}{c^2+d^2}i$
Bài tập:
Test24 | Phép chia số phức
Căn bậc 2:
Căn bậc 2 của số dương $d$ là: $\sqrt{d}$ và $-\sqrt{d}$
Căn bậc 2 của số âm $a$ là: $\sqrt{|a|}i$ và$-\sqrt{|a|}i$
Phương trình bậc 2:
$ax^2+bx+c=0$
- khi $\Delta =0$ thì có 1 nghiệm $x=\frac{-b}{2a}$
- khi $\Delta >0$ thì có 2 nghiệm $x=\frac{-b+\sqrt{\Delta }}{2a}$ và $x=\frac{-b-\sqrt{\Delta }}{2a}$
- khi $\Delta <0$ thì ko có nghiệm $x\in R$
Khi phương trình ko có nghiệm là số thực thì nó có 2 nghiệm là số phức:
$x=\frac{-b+\sqrt{|\Delta| }i}{2a}$ và $x=\frac{-b-\sqrt{|\Delta| }i}{2a}$
Bài tập:
Test25 | Phương trình bậc 2 với hệ số thực
Chương 7.
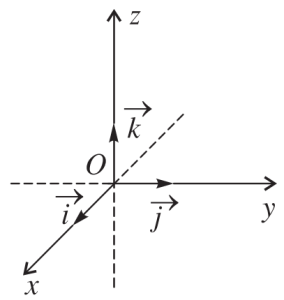
Các vector đơn vị: $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ có độ dài bằng 1.
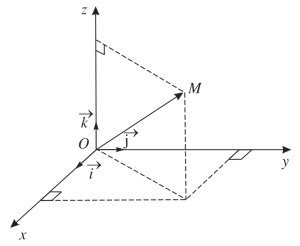
Tọa độ điểm $M= (x_M;y_M;z_M)$
Tọa độ của gốc tọa độ $O=(0;0;0)$
Tọa độ vector $\overrightarrow{AB}=B-A=(x_B-x_A;y_B-y_A;z_B-z_A)$
Tọa độ trung điểm đoạn $AB$ là: $\left ( \frac{x_A+x_B}{2};\frac{y_A+y_B}{2};\frac{z_A+z_B}{2} \right )$
$\overrightarrow{0}=(0;0;0)$
Tọa độ các vector đơn vị:
$\overrightarrow{i}=(1;0;0)$
$\overrightarrow{j}=(0;1;0)$
$\overrightarrow{k}=(0;0;1)$
$\overrightarrow{a}+\overrightarrow{b}=(x_a+x_b;y_a+y_b;z_a+z_b)$
$\overrightarrow{a}-\overrightarrow{b}=(x_a-x_b;y_a-y_b;z_a-z_b)$
$n.\overrightarrow{a}=(n.x_a;n.y_a;n.z_a)$ với $n$ là con số.
$\overrightarrow{a}=\overrightarrow{b}$ khi $x_a=x_b,y_a=y_b,z_a=z_b$
$\overrightarrow{a},\overrightarrow{b}$ cùng phương khi có số $k$ để $\overrightarrow{a}=k.\overrightarrow{b}$ (tức là tọa độ của $\overrightarrow{a}$ gấp $k$ lần tọa độ của $\overrightarrow{b}$).
Nếu $k$ dương thì $\overrightarrow{a},\overrightarrow{b}$ cùng hướng.
Nếu $k$ âm thì $\overrightarrow{a},\overrightarrow{b}$ ngược hướng.
Bài tập:
Test35 | Tọa độ điểm, vector
Tích vô hướng: $\overrightarrow{a}.\overrightarrow{b}=x_a.x_b+y_a.y_b+z_a.z_b$
Độ dài vector: $\left |\overrightarrow{a} \right |=\sqrt{x_a^2+y_a^2+z_a^2}$
Vì $\overrightarrow{a}.\overrightarrow{b}=\left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |.\cos\varphi $
nên $\cos\varphi =\frac{\overrightarrow{a}.\overrightarrow{b}}{\left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |}$
($\varphi $ là góc giữa 2 vector).
$\overrightarrow{a}\perp \overrightarrow{b}$ khi $\overrightarrow{a}.\overrightarrow{b}=0$
Bài tập:
Test36 | Tích vô hướng
Mặt cầu tâm $I$, bán kính $R$ có phương trình là: $(x-x_I)^2+(y-y_I)^2+(z-z_I)^2=R^2$.
Xét mặt cầu $(x-a)^2+(y-b)^2+(z-c)^3=d$.
- Điểm $M$ nằm trên mặt cầu nếu $(x_M-a)^2+(y_M-b)^2+(z_M-c)^3=d$.
- Điểm $M$ ko nằm trên mặt cầu nếu $(x_M-a)^2+(y_M-b)^2+(z_M-c)^3\neq d$.
Bài tập:
Test37 | Phương trình mặt cầu
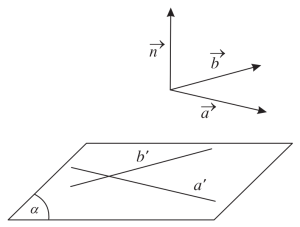
Tích có hướng của $\overrightarrow{a},\overrightarrow{b}$ là vector vuông góc với cả $\overrightarrow{a}$ và $\overrightarrow{b}$.
Kí hiệu: $\overrightarrow{n}=\overrightarrow{a}\wedge \overrightarrow{b}$ hoặc $\overrightarrow{n}=\left [\overrightarrow{a}, \overrightarrow{b} \right ]$.
Quy tắc 23-31-12:
Xét $\overrightarrow{a}(a_1;a_2;a_3),\overrightarrow{b}(b_1;b_2;b_3)$.
Tọa độ vector tích có hướng: $\overrightarrow{n}=\left [\overrightarrow{a}, \overrightarrow{b} \right ]=\left ( a_2.b_3-a_3.b_2;a_3.b_1-a_1.b_3;a_1.b_2-a_2.b_1 \right )$.
Bài tập:
Test44 | Tích có hướng
Vector pháp tuyến của mặt phẳng: khác $\overrightarrow{0}$, và vuông góc với mặt phẳng.
Nếu mặt phẳng $(P)$ chứa $\overrightarrow{a},\overrightarrow{b}$ ko cùng phương thì $\left [\overrightarrow{a}, \overrightarrow{b} \right ]$ là vector pháp tuyến của $(P)$.
Mặt phẳng đi qua điểm $M$ và có vector pháp tuyến $\overrightarrow{n}$ thì có phương trình là:
$x_n.(x-x_M)+y_n.(y-y_M)+z_n.(z-z_M)=0$
Phương trình tổng quát của mặt phẳng: $Ax+By+Cz+D=0$ với $A,B,C$ ko đồng thời bằng 0.
- Điểm $M$ nằm trên mặt phẳng nếu $Ax_M+By_M+Cz_M+D=0$
- Điểm $M$ ko nằm trên mặt phẳng nếu $Ax_M+By_M+Cz_M+D\neq 0$
Mặt phẳng đi qua gốc tọa độ:
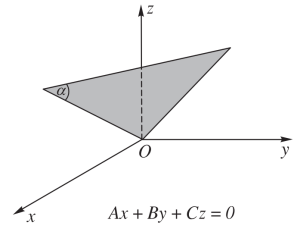
Mặt phẳng song song hoặc chứa 1 trục tọa độ: vector pháp tuyến song song với vector đơn vị.
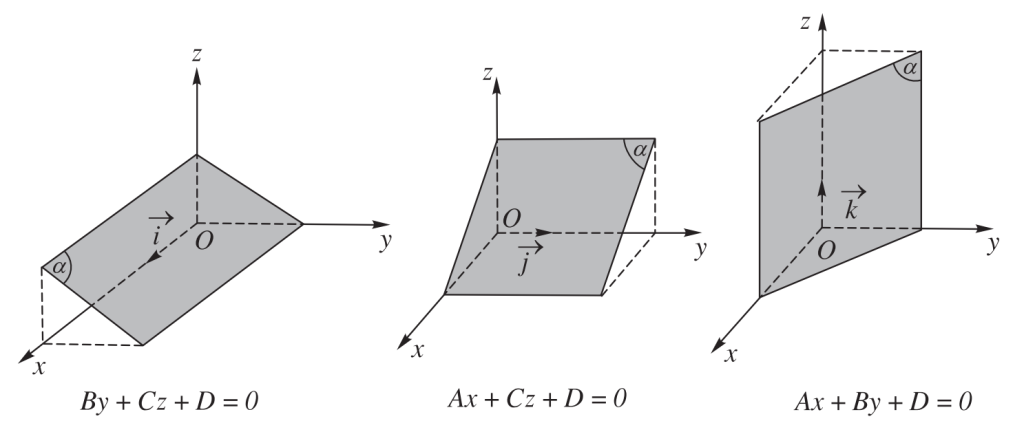
Mặt phẳng song song với 2 trục tọa độ:
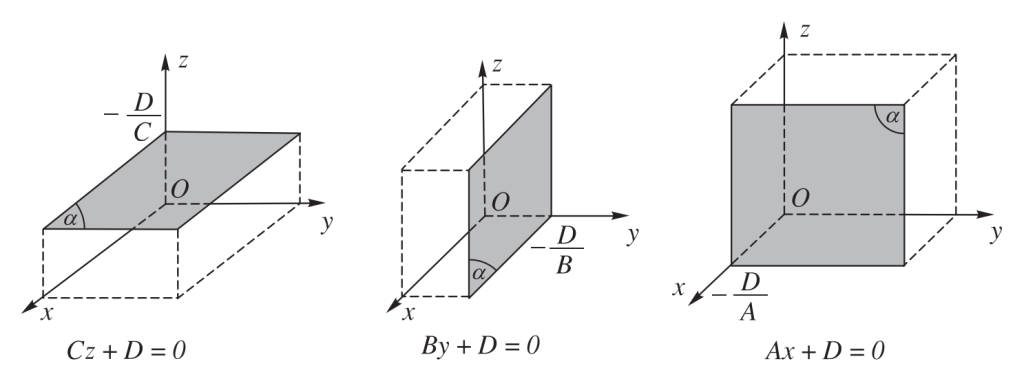
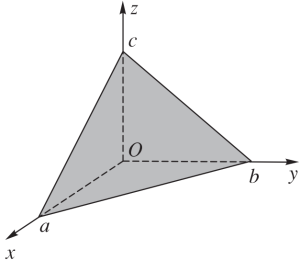
Phương trình mặt phẳng theo đoạn chắn:
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
Bài tập:
Test38 | Phương trình mặt phẳng
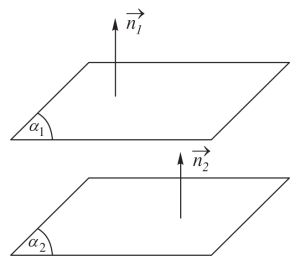
Hai mp song song hoặc trùng nhau nếu chúng có các pháp tuyến cùng phương.
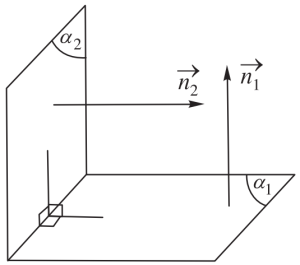
Hai mp vuông góc nhau nếu chúng có các pháp tuyến vuông góc nhau.
$\overrightarrow{a}\perp \overrightarrow{b}$ khi $\overrightarrow{a}.\overrightarrow{b}=0$.
Bài tập:
Test39 | Điều kiện để 2 mặt phẳng song song, vuông góc
Xét mp $(P)$ với phương trình $Ax+By+Cz+D=0$ và điểm $M$.
Khoảng cách từ $M$ đến $(P)$ là: $\displaystyle d\left ( M,(P) \right )=\frac{\left | A.x_M+B.y_M+C.z_M+D \right |}{\sqrt{A^2+B^2+C^2}}$
Bài tập:
Test40 | Khoảng cách từ 1 điểm đến 1 mặt phẳng
Xét đường thẳng $d$ đi quan điểm $M$, và có vector chỉ phương $\overrightarrow{c}$.
Phương trình tham số của $d$ là:
$\left\{\begin{matrix}x=x_M+x_c.t\\y=y_M+y_c.t\\z=z_M+z_c.t\end{matrix}\right.$
($t$ được gọi là tham số)
Xét đường thẳng với phương trình $\left\{\begin{matrix}x=a+u.t\\y=b+v.t\\z=c+w.t\end{matrix}\right.$
- Điểm $N$ nằm trên đường thẳng nếu hệ phương trình $\left\{\begin{matrix}x_N=a+u.t\\y_N=b+v.t\\z_N=c+w.t\end{matrix}\right.$ có nghiệm $t$.
- Điểm $N$ ko nằm trên đường thẳng nếu hệ phương trình $\left\{\begin{matrix}x_N=a+u.t\\y_N=b+v.t\\z_N=c+w.t\end{matrix}\right.$ ko có nghiệm $t$.
- ->(để giải hệ pt trên thì chỉ cần giải 1 pt rồi thay giá trị tìm được vào $t$ ở 2 pt còn lại -> nếu cả 2 pt đó đều cho 2 vế bằng nhau thì giá trị tìm được là nghiệm của hệ pt)
Phương trình đường thẳng dạng chính tắc:
$\frac{x-x_M}{x_c}=\frac{y-y_M}{y_c}=\frac{z-z_M}{z_c}$
Bài tập:
Test41 | Phương trình đường thẳng
Hai đường thẳng song song khi các vector chỉ phương cùng phương với nhau, và điểm $M$ chỉ nằm trên 1 trong 2 đường thẳng.
Xét 2 đường thẳng $d$ và $d’$ với các phương trình tham số là:
$\left\{\begin{matrix}x=a+u.t\\y=b+v.t\\z=c+w.t\end{matrix}\right.$
và $\left\{\begin{matrix}x=a’+u’.t\\y=b’+v’.t\\z=c’+w’.t\end{matrix}\right.$
Hai đường thẳng cắt nhau khi chúng chỉ có 1 điểm chung. Tức là hệ phương trình:
$\left\{\begin{matrix}a+u.t=a’+u’.t’\\b+v.t=b’+v’.t’\\c+w.t=c’+w’.t’\end{matrix}\right.$
có duy nhất 1 bộ nghiệm $(t;t’)$.
(Chú ý $t$ ở phương trình của đường thẳng thứ 2 được thay bằng $t’$).
Hai đường thẳng chéo nhau khi hệ phương trình trên vô nghiệm.
Bài tập:
Test42 | Điều kiện để 2 đường thẳng song song, cắt nhau, chéo nhau
Xét mặt phẳng $(\alpha ): Ax+By+Cz+D=0$
và đường thẳng $d$:
$\left\{\begin{matrix}x=a+u.t\\y=b+v.t\\z=e+w.t\end{matrix}\right.$
Thay các $x,y,z$ của $d$ vào phương trình của $(\alpha )$:
$A(a+u.t)+B(b+v.t)+C(e+w.t)+D=0$.
Xét phương trình trên với nghiệm là $t$:
- Nếu pt vô nghiệm thì $d // (\alpha )$
- Nếu pt có 1 nghiệm thì $d$ cắt $(\alpha )$
- Nếu pt có vô số nghiệm thì $d$ nằm trên $(\alpha )$
Bài tập:
Test43 | Mặt phẳng và đường thẳng